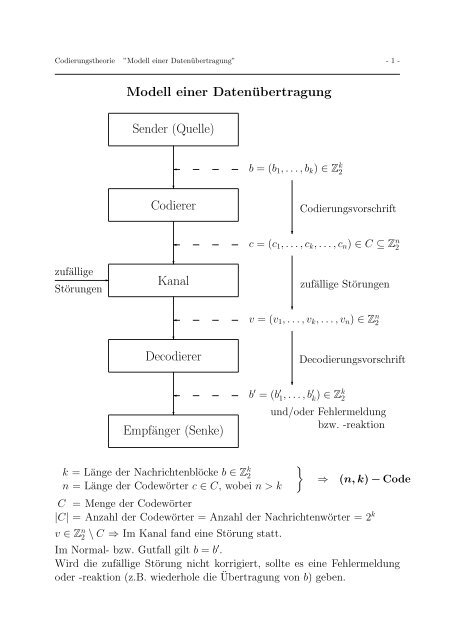
Modell einer Datenübertragung Sender (Quelle) Codierer Kanal ...

Codierungstheorie ”Modell einer Datenübertragung” - 1 -
zufällige
Störungen
✲
Modell einer Datenübertragung
Sender (Quelle)
✛
❄
b = (b1, . . . , bk) ∈ Z k 2
Codierer Codierungsvorschrift
✛
❄
❄
c = (c1, . . . , ck, . . . , cn) ∈ C ⊆ Z n 2
Kanal zufällige Störungen
✛
❄
❄
v = (v1, . . . , vk, . . . , vn) ∈ Z n 2
Decodierer Decodierungsvorschrift
✛
❄
Empfänger (Senke)
k = Länge der Nachrichtenblöcke b ∈ Z k 2
n = Länge der Codewörter c ∈ C, wobei n > k
❄
b ′ = (b ′ 1, . . . , b ′ k ) ∈ Zk 2
und/oder Fehlermeldung
bzw. -reaktion
�
⇒ (n, k) − Code
C = Menge der Codewörter
|C| = Anzahl der Codewörter = Anzahl der Nachrichtenwörter = 2 k
v ∈ Z n 2 \ C ⇒ Im Kanal fand eine Störung statt.
Im Normal- bzw. Gutfall gilt b = b ′ .
Wird die zufällige Störung nicht korrigiert, sollte es eine Fehlermeldung
oder -reaktion (z.B. wiederhole die Übertragung von b) geben.

Codierungstheorie ”Bemerkungen” - 2 -
Kanal = z.B. physikalische Leitung oder
ein Speicher, aus dem die Zeichen nach einer
gewissen Zeit wieder abgerufen werden.
Zufällige Störungen werden verursacht z.B. durch
-) den sporadischen Einfluss von elektromagnetischen Feldern auf
elektrische Datenleitungen,
-) den α-Teilchen Beschuss von Speicherbausteinen,
-) Kratzer oder Fingerabdrücke auf CDs oder DVDs.
Beispiele für Anwendungsgebiete von Codierungsverfahren sind:
-) Datenübertragung (Häufig werden verwendet:
CRC-Codes = Cyclic Redundancy Check Codes)
-) RAM-Chipsätze und L2-Cache ab Pentium-II, 300 Mhz
(ECC = Error Correcting Code
auf Basis eines binären Hamming-Codes.
Literaturhinweis: c’t 12/1998, S. 232)
-) CDs (CIRC = Cross Interleaved Read-Solomon Code)
-) DVDs (RS-PC = Read-Solomon-Produkt-Code)
Vereinfachung der Notation in diesem Kapitel:
Statt (b1, . . . , bk) und (c1, . . . , cn) wird häufig einfacher b1 . . . bk
bzw. c1 . . . cn geschrieben.
Die Addition modulo 2 wird in diesem Kapitel mit ⊕ bezeichnet.
Zwei Bitblöcke werden bzgl. ⊕ bitweise addiert, z.B.
10011 ⊕ 11001 = 01010. (kein Übertrag !)
Die Verknüpfung ⊕ ist selbstinvers, da z.B. gilt
10011 ⊕ 10011 = 00000.

Codierungstheorie ”Definition des Hamming-Abstandes” - 3 -
Definition 5.1
Definition des Hamming-Abstandes
a) Es seien a = a1a2 . . . an ∈ Z n 2 und b = b1b2 . . . bn ∈ Z n 2.
Dann definieren
i) d(a, b) = ”Anzahl der Bits, in denen sich
a und b unterscheiden ”
den Abstand von a und b,
ii) w(a) = ”Anzahl der Einsen von a ”
das Gewicht von a.
b) Es sei C ⊆ Z n 2. Dann definiert
d(C) = min{ d(a, b) : a, b ∈ C , a �= b }
den Hamming-Abstand eines Codes (mit Codewörtern
aus) C.
Der Abstand und das Gewicht hängen wie folgt zusammen:
Satz 5.1
Für alle a = a1a2 . . . an ∈ Z n 2 und b = b1b2 . . . bn ∈ Z n 2 gilt:
Beweis:
d(a, b) = w(a ⊕ b).
Wegen 0 ⊕ 0 = 0, 1 ⊕ 0 = 1, 0 ⊕ 1 = 1 und 1 ⊕ 1 = 0
gilt für jeden Index i mit 1 ≤ i ≤ n:
ai und bi sind verschieden ⇔ ai ⊕ bi = 1.

Codierungstheorie ”Das ML-Prinzip” - 4 -
Das Maximum-Likelihood-Decodierungsprinzip
Bei der Decodierung gehen wir von folgender Annahme aus:
Annahme:
Ein Zeichen in einem Bitblock wurde eher richtig als falsch empfangen.
Somit ist es sinnvoll, (fehlerhafte) Bitblöcke nach folgendem Prinzip
zu decodieren:
Maximum-Likelihood-Decodierungsprinzip (ML-Prinzip):
Wir ordnen einem empfangenen v ∈ Z n 2 das c ′ ∈ C zu, für das der
Abstand d( v, c ′ ) über C minimal ist, d.h.
d( v, c ′ ) = min{ d( v, c) : c ∈ C },
und decodieren dann c ′ ∈ C.
Ist c ′ ∈ C nicht eindeutig, so decodieren wir nicht (und geben z.B.
stattdessen eine Fehlermeldung aus) oder wir legen uns auf eine
Möglichkeit fest (evtl. nach anderen Kriterien).
Unter der Annahme des ML-Prinzips bestimmt der Hamming-
Abstand die Anzahl der Fehler, die (mit Sicherheit) korrigiert bzw.
erkannt werden können:
Satz 5.2
Es sei ein Code gegeben, dessen Codewörter C den Hamming-Abstand
d haben.
a) Ist d = 2m + 1 ungerade, so können m Fehler nach dem
ML-Prinzip eindeutig korrigiert werden.
b) Ist d = 2m + 2 gerade, so können m Fehler nach dem ML-
Prinzip eindeutig korrigiert werden und zusätzlich Bitblöcke
mit m + 1 Fehlern erkannt werden.

Codierungstheorie ”Lineare Codes” - 5 -
Lineare Codes
Definition 5.2
Lässt sich die Codierungsvorschrift eines (n, k)−Codes durch eine
k × n−Matrix G beschreiben,
d.h. gilt für alle Nachrichtenblöcke b und ihre dazugehörigen Codeworte
c die Beziehung c = b · G bzw. ausführlich
⎛
⎞
g11 g12 · · · g1k · · · g1n
(c1, . . . , ck, . . . , cn)
� �� �
c
= (b1, . . . , bk) ·
� �� �
b
⎜
⎝
g21 g22 · · · g2k · · · g2n
· · · · · · · · · · · · · · · · · ·
gk1 gk2 · · · gkk · · · gkn
⎟
⎟,
⎠
� �� �
G
so heißt G Generatormatrix dieses Codes und der Code wird
als linearer Code bezeichnet.
Die Codewörter C eines von einer Generatormatrix G erzeugten
Codes haben folgende Eigenschaft:
(5.1) c, f ∈ C ⇒ c ⊕ f ∈ C,
denn:
c, f ∈ C ⇒ es existieren b, a ∈ Z k 2 mit c = b · G und f = a · G
⇒ c ⊕ f = b · G ⊕ a · G = (b ⊕ a) · G ∈ C
Da außerdem (0, . . . , 0)
� �� �
n−mal
= (0, . . . , 0) · G ∈ C gilt, folgt:
� �� �
k−mal
Satz 5.3
Die Codewörter C eines linearen (n, k)−Codes bilden eine
Untergruppe der Gruppe (Z n 2, ⊕).

Codierungstheorie ”Der Hamming-Abstand eines linearen Codes” - 6 -
Der Hamming-Abstand eines linearen Codes
Satz 5.4
Für einen linearen Code mit Codewörtern C gilt
Beweis:
d(C) = min{ w(c) : c ∈ C , c �= 0 }
d(a, b) = w(a ⊕ b) gemäß Satz 5.1 und
{ a ⊕ b : a, b ∈ C, a �= b }
� �� �
M1
= { c : c ∈ C, c �= 0 }
� �� �
Diese Mengengleichheit ergibt sich aus folgenden Überlegungen:
”⊇”: c ∈ M2 ⇒ c = c
����
=a
⊕ ���� 0 ∈ M1
=b
Dies gilt, da C linear ist und somit 0 ∈ C.
Außerdem ist ���� c �=
=a
0 , da c ∈ M2.
����
=b
”⊆”: a ⊕ b ∈ M1 ⇒ c = a ⊕ b ∈ M2
Dies gilt, da C linear ist und somit c = a ⊕ b ∈ C.
Außerdem ist c = a ⊕ b �= 0, da a �= b.
Insgesamt folgt:
d(C) = min{ d(a, b) : a, b ∈ C , a �= b }
= min{ w(a ⊕ b) : a, b ∈ C , a �= b } (Satz 5.1)
= min{ w(c) : c ∈ C , c �= 0 } (M1 = M2)
M2

Codierungstheorie ”Die Kontrollmatrix” - 7 -
Die Kontrollmatrix
Definition 5.3
Eine (n−k)×n−Matrix H heißt Kontrollmatrix eines linearen
(n, k)−Codes mit Codewörtern C, falls für alle v ∈ Zn 2 gilt:
v ∈ C ⇔ H · vT ⎛ ⎞ ⎫
0.
⎬
= 0 = ⎝ ⎠ (n − k) − mal
⎭
0
Für lineare Codes, die eine spezielle Generatormatrix haben, kann
man sehr leicht eine Kontrollmatrix finden.
Satz 5.5
Ein linearer (n, k)−Code mit Codewörtern C habe die Generatormatrix
G = (Ek | A). Dann ist die Matrix
H = (A T | En−k)
eine Kontrollmatrix dieses Codes.
Beweisidee:
Da jedes v ∈ C eine Linearkombination von Zeilenvektoren der Generatormatrix
G ist, reicht es H·v T = 0 für die Zeilenvektoren von G nachzuweisen.
Wir zeigen dies exemplarisch für den 1. Zeilenvektor von G, d.h.
v = � �
1 0 · · · 0 a11 a12 · · · a1(n−k) Es gilt:
⎛
1
⎞
⎛
a11 a21 · · · ak1
⎜ a12 a22 · · · ak2
⎜
⎝ . . . .
a1(n−k) a2(n−k) · · · ak(n−k) � ��
=H
⎜
⎞ ⎜ 0.
⎟ ⎛
⎞
1 0 · · · 0 ⎜ ⎟
⎜ ⎟ a11 ⊕ a11
0 1 · · · 0
⎟ ⎜ ⎟ ⎜
⎟ ⎜ 0 ⎟ ⎜ a12 ⊕
⎟
a12 ⎟
⎟ · ⎜ ⎟ = ⎜
⎟
. . . . ⎠ ⎜ a11 ⎟ ⎝ . ⎠
⎜ ⎟
0 0 · · · 1 ⎜ a12 ⎟
� ⎜ ⎟
a1(n−k) ⊕ a1(n−k) ⎝ . ⎠ � �� �
=0
a1(n−k)

Codierungstheorie ”Nebenklassen von Codewörtern” - 8 -
Nebenklassen von Codewörtern
Für den Rest dieses Kapitels ist ein linearer (n, k)−Code mit
Codewörtern C und (fester) Kontrollmatrix H gegeben.
Satz 5.3 ⇒ (C, ⊕) ist eine Untergruppe der Gruppe (Z n 2, ⊕)
Definition 4.6 ⇒ a ⊕ C = {a ⊕ c : c ∈ C} heißt
(Links-)Nebenklasse von a bzgl. C
Da ⊕ kommutativ ist, gilt a ⊕ C = C ⊕ a für alle a ∈ Z n 2 und
daher sprechen wir nur von Nebenklassen.
Satz 4.5, b) ⇒ Nebenklassen sind entweder
disjunkt oder identisch
Satz 4.5, c) ⇒ |a ⊕ C| = |C| für alle a ∈ C
Satz 4.6 ⇒ I = Anzahl der Nebenklassen = |Zn 2|
|C|
2n
= = 2n−k
2k Somit kann Z n 2 in I = 2 n−k gleich große Nebenklassen zerlegt
werden:
(5.2) Z n 2 = (a1 ⊕ C) ∪ (a2 ⊕ C) ∪ . . . (aI ⊕ C)
a1 ⊕ C
(= C)
e�
v�
a2 ⊕ C
a4 ⊕ C
a3 ⊕ C
Venn-Diagramm zur Zerlegung von Z n 2 in 4 gleich große Nebenklassen
Z n 2

Codierungstheorie ”Nebenklassen und Fehlervektoren” - 9 -
Nebenklassen und Fehlervektoren
Annahme:
v ∈ Z n 2 wurde (evtl. verfälscht) empfangen.
Wegen (5.2) existiert dann ein ai mit v ∈ ai ⊕ C, d.h.
(5.3) v = ai ⊕ ˜c für ein ˜c ∈ C.
Sei c ∈ C das ursprüngliche Codewort und e ∈ Z n 2 der bei der
Übertragung aufgetretene Fehlervektor. Dann gilt:
(5.4) v = e ⊕ c
Zusammen ergeben (5.3) und (5.4):
e ⊕ c = v = ai ⊕ ˜c
⇒ e = e ⊕ c ⊕ c
� �� �
=0
= ai ⊕ ˜c ⊕ c
� �� �
∈C
∈ ai ⊕ C
Somit haben wir folgendes Resultat gezeigt:
Satz 5.6
Der Fehlervektor e eines empfangenen Bitblocks v ∈ ai ⊕ C liegt
in genau derselben Nebenklasse ai ⊕ C, in der v liegt.
Dieser Satz und das ML-Decodierungsprinzip ergeben folgende
Decodierungsregel (Variante mit Nebenklassenbestimmung)
Bestimme diejenige Nebenklasse ai ⊕ C, für die v ∈ ai ⊕ C gilt.
Wähle dann f ∈ ai ⊕ C mit minimalem Gewicht. Decodiere v
durch c = f ⊕ v.
Begründung, dass diese Regel sinnvoll ist:
Nach dem ML-Prinzip gilt mit hoher Wahrscheinlichkeit f = e
und damit folgt wegen (5.4):
f ⊕ v = e ⊕ v = e ⊕ e ⊕ c = c.

Codierungstheorie ”Das Standardfeld” - 10 -
Das Standardfeld
Die Decodierung nach der Decodierungsregel der vorherigen Seite
lässt sich mit Hilfe eines Standardfeldes durchführen. Dazu sei
C = {0, c1, c2, c3, . . .}
die Menge der Codewörter und für jede Nebenklasse
ai ⊕ C , wobei 1 ≤ i ≤ I = 2 n−k
gelte die Darstellung, dass ai ein Element mit minimalem Gewicht
in dieser Nebenklasse ist. ai heißt der Klassenanführer
dieser Nebenklasse.
Gibt es mehrere Möglichkeiten für den Klassenanführer, so muss
der Klassenanführer nach zusätzlichen Kriterien oder willkürlich
aus diesen Möglichkeiten ausgewählt werden.
Das Standardfeld hat dann folgende Darstellung:
a1 = 0 c1 c2 c3 . . . C = a1 ⊕ C
a2 a2 ⊕ c1 a2 ⊕ c2 a2 ⊕ c3 . . . a2 ⊕ C
a3 a3 ⊕ c1 a3 ⊕ c2 a3 ⊕ c3 . . . a3 ⊕ C
. . . . . . . . . . . . . . .
aI aI ⊕ c1 aI ⊕ c2 aI ⊕ c3 . . . aI ⊕ C
Ein Vektor v = ai ⊕ cj ∈ ai ⊕ C wird im Standardfeld durch den
Spaltenkopf ai ⊕ v = ai ⊕ ai ⊕ cj = cj decodiert.
Satz 5.7
Die Fehlervektoren, die mit einem Standardfeld korrigiert werden,
sind genau die Klassenanführer.

Codierungstheorie ”Das Syndrom” - 11 -
Das Syndrom
Definition 5.4
Gegeben sei ein linearer (n, k)−Code mit Kontrollmatrix H. Dann
ist das Syndron s eines Vektors v ∈ Z n 2 definiert durch
Satz 5.8
s = H · v T .
a) Enthält v ∈ Z n 2 genau an den Stellen i, j, k, . . . Fehler, so gilt
für das Syndrom
s = hi ⊕ hj ⊕ hk ⊕ . . .,
wobei hi, hj, hk, . . . die i-te, j-te, k-te, . . . Spalte der Matrix
H sind.
b) Zwei Vektoren v1, v2 ∈ Z n 2 liegen genau dann in derselben
Nebenklasse von C, wenn sie dasselbe Syndrom haben.
Beweis zu b):
a) v1, v2 liegen in derselben Nebenklasse
⇒ es exist ein ai mit v1, v2 ∈ ai ⊕ C
⇒ es exist c1, c2 ∈ C mit v1 = ai ⊕ c1 und v2 = ai ⊕ c2
⇒ s1 = Hv T 1 = Ha T i ⊕ HcT 1
����
=0
= HaT i = HaTi ⊕ HcT ���� 2 = Hv
=0
T 2 = s2
b) v1, v2 haben dasselbe Syndrom, d.h. Hv T 1 = Hv T 2
⇒ 0 = Hv T 2 ⊕ Hv T 1 = H(v2 ⊕ v1) T ⇒ v2 ⊕ v1 ∈ C
Zu zeigen: v1 ∈ ai ⊕ C ⇒ v2 ∈ ai ⊕ C
denn: v1 ∈ ai ⊕ C ⇒ es exist ein c1 ∈ C mit v1 = ai ⊕ c1
∈C
���� � �� �
⇒ v2 = v1 ⊕ (v2 ⊕ v1) = ai ⊕ c1 ⊕ (v2 ⊕ v1) ∈ ai ⊕ C
� �� �
∈C
∈C

Codierungstheorie ”Die Syndromtabelle” - 12 -
Die Syndromtabelle
Wegen Satz 5.8, b) kann man Nebenklassen durch ihre Syndrome
charakterisieren.
Zur Decodierung mittels Syndromen benötigt man daher anstelle
des Standardfeldes lediglich eine Tabelle, genannt Syndromtabelle,
in der jedem Syndrom der entsprechende Klassenanführer
zugeordnet wird.
Wir erhalten somit folgende
Decodierungsregel (Variante mit Syndromberechnung)
Berechne zu v das Syndrom s = H · v T . Entnehme dann der Syndromtabelle
den zu s gehörigen Klassenanführer ai. Decodiere v
durch c = ai ⊕ v.

Codierungstheorie ”Anhang 1: Der (7,4)-Hamming-Code” - 13 -
Codierungsvorschrift:
Der (7,4)-Hamming-Code
b1 b2 b3 b4 ↦−→ c1 c2 c3 c4 c5 c6 c7
mit c1 = b1, c2 = b2, c3 = b3, c4 = b4 und folgenden 3 Paritätsgleichungen:
c5 = b1 ⊕ b2 ⊕ b3,
Decodierungsvorschrift:
c6 = b1 ⊕ b2 ⊕ b4,
c7 = b1 ⊕ b3 ⊕ b4.
v = v1 v2 v3 v4 v5 v6 v7 wurde empfangen. Aus der Codierungsvorschrift
ergeben sich 3 Kontrollgleichungen:
s1 = v1 ⊕ v2 ⊕ v3 ⊕ v5,
s2 = v1 ⊕ v2 ⊕ v4 ⊕ v6,
s3 = v1 ⊕ v3 ⊕ v4 ⊕ v7.
Diese Kontrollgleichungen liefern folgende Syndromtabelle:
s1 s2 s3
kein Fehler 0 0 0
1. Stelle falsch 1 1 1
2. Stelle falsch 1 1 0
3. Stelle falsch 1 0 1
4. Stelle falsch 0 1 1
5. Stelle falsch 1 0 0
6. Stelle falsch 0 1 0
7. Stelle falsch 0 0 1