FH D FB 4 - Informatik

FH D
Lehr- und Forschungsgebiet Informatik I
FB 4
Laborversuch Nr. 3
Kontrollstrukturen 2 (Schleifen)
for while do
while
Lin. 10/2010
- 35 -

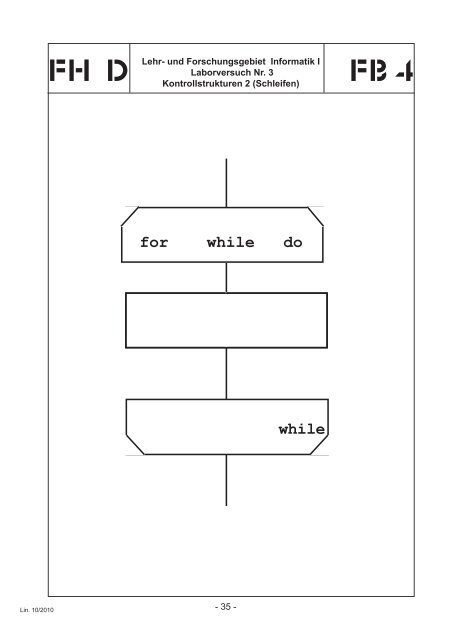
3 Zyklische Struktur (Schleife)
Die zyklische Struktur erlaubt es, Programmteile mehrfach in Abhängigkeit einer
Bedingung zu durchlaufen. Erst dadurch lassen sich viele Probleme mit einem vertretbaren
Programmieraufwand lösen. Die folgende Abbildung zeigt die graphischen
Darstellungsformen für die zyklische Struktur.
Programmablaufplan
Struktogramm
Schleifenanfang
Schleifenbereich
Anweisung(en)
Anweisung(en)
Schleifenende
Abb. 3.1: Schleifendarstellungen
Die zyklische Struktur kann mit den Sprachmitteln aus Verzweigung und Rücksprung
realisiert werden. Darüber hinaus gibt es noch weitere Schleifen-Anweisungen. Diese
können unterteilt werden in Anweisungen für Zählschleifen und Anweisungen für
Bedingungsschleifen.
3.1 Zählschleifen
Für Zählschleifen wird die Konstruktion mit for gewählt. Diese hat die allgemeine
Form:
for (Ausdruck1; Bedingung; Ausdruck3)
Anweisung;
Hierbei wird über den Ausdruck1 der Zählvariablen ein Anfangswert zugewiesen; die
Bedingung prüft den Wert der Laufvariablen; Ausdruck3 bewirkt eine Veränderung
des Wertes um die Schrittweite. Solange die Bedingung erfüllt ist, wird die angegebene
Anweisung wiederholt ausgeführt.
Lin. 10/2010
- 36 -

Das Bild zeigt die graphische Darstellung in Form eines Programmablaufplans und
Struktogramms.
for (a1;b;a3)
for (a1;b;a3)
Abb. 3.2: Zählschleife
Bei Zählschleifen muss die Zählervariable verändert werden. Beim Inkrementieren
(incrementare (lat.) = um einen bestimmten Wert erhöhen) oder Dekrementieren wird
der Wert um einen festen Betrag (oftmals eins) erhöht bzw. verringert. Als Anweisung
geschrieben:
z = z + x; oder z = z - x;
In C läßt sich dieser Ausdruck vereinfachen zu:
z += x ; oder z -= x;
In C läßt sich dieser Ausdruck für den Zuwachs um 1 weiter vereinfachen zu:
z++; oder z--;
3.2 Sprachmittel für Bedingungsschleifen
Bei Bedingungsschleifen ist die Anzahl der Schleifendurchläufe nicht bekannt. Für die
bedingungsgesteuerten Schleifen gibt es zwei verschiedene Arten der Realisierung.
3.2.1 Bedingungsschleife mit Bedingungstest am Anfang
Bei der Bedingungsschleife mit der Bedingung am Anfang wird ein Ausdruck auf true
oder false überprüft, bevor die Schleifenanweisung durchlaufen wird. Damit hat diese
Form der Bedingungsschleife einen abweisenden Charakter.
Die Schleife mit while hat grundsätzlich folgendes Aussehen:
while (Bedingung)
Anweisung;
Lin. 10/2010
- 37 -

Solange der Ausdruck (Bedingung) hinter while den Wert true hat, wird die Anweisung
wiederholt ausgeführt. Liefert der angegebene Ausdruck den Wert false, wird
im Programm fortgefahren.
Statt einer einzelnen Anweisung können auch mehrere Anweisungen stehen, die in
geschweifte Klammern gesetzt werden (Block).
while (Bedingung)
Anweisung(en);
Abb. 3.3: Die Bedingungsschleife mit Bedingungstest am Anfang
3.2.2 Bedingungsschleife mit Bedingungstest am Ende
Im Gegensatz zur einfachen while-Schleife wird die Anweisung zunächst ausgeführt,
dann erst wird geprüft, ob die Schleife wiederholt werden soll. Die Schleife wird also
auf jeden Fall mindestens einmal durchlaufen, da die Abfrage erst am Ende steht. Sie
hat also keinen abweisenden Charakter.
Die allgemeine Form lautet:
do
Anweisung;
while (Bedingung);
Anweisung(en);
while (Bedingung)
Abb. 3.4: Bedingungsgesteuerte Schleife mit Bedingungstest am Ende
Lin. 10/2010
- 38 -

3.3 Folgen und Reihen
3.3.1 Definition
Gegeben sei eine Folge (a n
) = a 1
, a 2
, a 3
, ...
Dann nennt man die Folge (s n
) = s 1
, s 2
, s 3
, ...,
deren Elemente s n
nach der Vorschrift:
s n
= a 1
+ a 2
+ ... + a n
gebildet werden, die Reihe (s n
) der Folge (a n
).
Anstatt Reihe sagt man auch Teilsummenfolge.
Erläuterung der Definition
Gegeben sei eine Folge (a n
) = n·2 = 2, 4, 6, 8, 10, 12, ...
Nur bilden wir die Summen s n
aus den ersten n-Gliedern
dieser Folge:
Die Summe s 1
besteht nur aus einem Summanden (2)
Die Summe s 2
entsteht durch Addition der ersten zwei Glieder
Die Summe s 3
entsteht durch Addition der ersten drei Glieder
Die Summe s 4
entsteht durch Addition der ersten vier Glieder
s 1
= 2 = 2
s 2
= 2 + 4 = 6
s 3
= 2 + 4 + 6 = 12
s 4
= 2 + 4 + 6 + 8 = 20
s 5
= 2 + 4 + 6 + 8 +10 = 30
usw.
Dann kann man die Summen s n
als eine neue Folge (s n
)
betrachten: (s n
) = 2, 6, 12, 20, 30, ...
Diese Folge hat nun einen besonderen Namen: Weil sie aus den Teilsummen
gebildet wird, nennt man sie Teilsummenfolge oder Reihe.
3.3.2 Reihenentwicklung
Eine Reihenentwicklung ermöglicht in der Mathematik die Berechnung einer
nicht direkt mit elementaren Operationen (Addition, Subtraktion, Multiplikation
und Division) darstellbaren mathematischen Funktion durch eine endliche oder
unendliche Summe von elementaren Ausdrücken. Diese so genannte Reihe kann
in der Praxis oft auf endliche viele Glieder reduziert werden, wodurch eine Näherung
der exakten Funktion entsteht, die umso einfacher ist, je weniger Glieder genommen
wurden, aber umso besser ist, je mehr genommen wurden. Häufig lässt sich die dadurch
entstandene Ungenauigkeit (also die Größe des Restgliedes) formelhaft beschreiben.
Bei einer erzeugenden Funktion erscheinen die Glieder einer unendliche
Folge als Koeffizienten der Reihenentwicklung.
In der Mathematik tauchen zum Beispiel folgende Reihenentwicklungen auf:
Taylorreihe (Potenzreihe),Maclaurin-Reihe, Fourierreihe, Falkultätsreihe.
Lin. 10/2010
- 39 -

3.4 Beispiele für Schleifen-Struktur
3.4.1 Aufgabenstellung
Als Beispiel soll die Summe der natürlichen Zahlen von 1 bis n ermittelt werden.
3.4.2 Problemanalyse
Es handelt sich hierbei um das Problem, Folgenelemente zu erzeugen und diese
arithmetisch zu verknüpfen. Die Betrachtung gilt also grundsätzlich für die Problemklasse
Folgen und Reihen.
Eingabe:
Ausgabe:
natürliche Zahl n
Summe der natürlichen Zahlen s
3.4.3 Algorithmus
Die Aufgabe läßt sich mathematisch wie folgt formulieren:
n
s = ∑ i mit i, n ∈|N
i=1
Diese Formulierung läßt sich leider so nicht direkt umsetzen. Um den Algorithmus zu
finden, sieht man sich am besten die Teilsummen an:
s 0
= 0
s 1
= 0+1 = s 0
+ 1 = s 0
+ m 1
s 2
= 0+1+2 = s 1
+ 2 = s 1
+ m 2
s 3
= 0+1+2+ 3 = s 2
+ 3 = s 2
+ m 3
.
.
.
s n
= 0+1+2+... + n = n n-1
+ n = s n-1
+ m n
Aus der Aufstellung erkennt man folgende Zusammenhänge als Bildungsgesetz für
alle entsprechenden Aufgaben:
1. Festlegen der Anfangswerte von m und s
2. m i
= m i-1
+ 1 (Bildungsgesetz für Folgenelement)
3. s i
= s i-1
+ m i
(Teilsummenbildung, da arithmetische Reihe)
4. Dieser Ablauf hat solange zu erfolgen, bis m i
= n ist (Endekriterium)
Lin. 10/2010
- 40 -

3.4.4 Graphische Darstellung des Programms "Summe der natürlichen Zahlen":
Programmablaufplan
Anfang
Eingabe: n
s=0
for(m=1;m

3.4.6 Die Ausführung
3.4.7 N-Fakultät
Die Fakultät ist in der Mathematik eine Funktion, die als das Produkt aller natürlichen
Zahlen kleiner oder gleich dieser Zahl N definiert ist. Sie wird durch ein dem Argument
nachgestelltes Ausrufezeichen („!“) abgekürzt.
Für alle natürlichen Zahlen n ist:
n! = 1 * 2 * 3 * 4 * ...........* (n-1) * n ; außerdem ist: 0!=1.
Das folgende Listing zeigt dieses Programm.
/*Fakultät*/
/*Autor: A.Linder, Oktober 2010*/
#include
void main()
{
int n, m;
double p;
printf("*************************************\n");
printf("* N-Fakultaet *\n");
printf("* Autor: Alfred Linder *\n");
printf("*************************************\n\n");
printf("Bitte geben Sie n an! ");
scanf ("%i", &n);
p = 1;
for(m = 1; m

3.5 Aufgabe
Erstellen Sie je ein Schleifen-Programm zur Berechnung der Reihe, die der Endziffer
Ihrer Matrikelnummer entspricht (siehe Seite 44). Hierzu verwenden Sie bitte nur die
elementare Arithmetik und Logik, keine mathematischen Funktionen.
Das Endekriterium für Programm 1 ist die Anzahl der Schleifendurchläufe n. Hierzu
wählen Sie Ihre Matrikelnummer (n=Matrikelnummer). Zum Nachweis der Korrektheit
zeigen Sie das Ergebnis der ersten drei Teilsummen und das Ergebnis für
n=Matrikelnummer.
Das Endekriterium für Programm 2 ist die Vorgabe eines relativen Fehlers rf. Hierzu
wählen Sie den Kehrwert Ihrer Matrikelnummer (rf=1/Matrikelnummer).
Diese Aufgabe ist eine Hausaufgabe. Sie sollen diese Hausaufgabe selbstständig
bearbeiten und lösen. Alle Lösungen, die vermuten lassen, dass die Bearbeitung
nicht eigenständig durch Sie selbst erfolgte, werden mit 0 Punkten bewertet oder
zumindest stark abgewertet. Diese Abwertung betrifft auch diejenigen Lösungen, die
als Quelle für andere abgegebene Lösungen vermutet werden können.
Das Programm einschließlich vollständiger Dokumentation (auf Papier, nicht auf Datenträger)
ist spätestens am 8.11.2010, 8.00 Uhr im Raum S4, oder Postfach
von A. Linder) abzugeben.
Zu einer vollständigen Dokumentation (angelehnt an DIN 66230) gehören:
1. Deckblatt mit Name, Matrikelnummer und Gruppe.
2. Kurzbezeichnung des Programmes
Diese Kurzbezeichnung soll beim Start des Programmes u.a. erscheinen.
3. Aufgabe des Programms
Kurze anwendungsbezogene Beschreibung der Aufgabe, die mit dem Programm
gelöst wird (inkl. Beschreibung der Programmeingaben und –Ausgaben)
4. Aufgabenlösung
Kurze Beschreibung der zur Lösung der Aufgabe verwendeten Methoden,
Theorien und Berechnungsverfahren (Algorithmen).
5. Grafische Darstellung des Programmablaufs
Struktogramm (DIN 66261) oder Programmablaufplan (DIN 66001).
6. Programmausdruck
"Listing" der fehlerfreien C-Quellprogramme mit Angabe des Autors als Kommentar
im Quellcode.
7. Testlauf
Screenshots der Konsolfenster für einen vollständigen Programmablauf (beim
Starten muss das Programm u.a. den Namen und die Matrikelnummer des Autors
ausgeben).
Lin. 10/2010
- 43 -

Gegebene Reihen:
Lin. 10/2010
- 44 -