Kapitel 3 Modellierung elektrohydraulischer Bauteile - ACIN

Kapitel 3 

Modellierung elektrohydraulischer 

Bauteile 

Nachdem im vorigen Kapitel die Grundlagen zur Beschreibung einer Strömung anhand 

der Bilanzgleichungen sowie der Materialmodelle erfolgte, beschäftigt sich dieses Kapitel 

mit der mathematischen Modellierung der wichtigsten (elektro-)hydraulischen Bauteile. 

3.1 Konstantes hydraulisches Volumen 

Das einfachste hydraulische Bauteil ist ein konstantes Volumen, welches mit Hydraulikflüssigkeit 

gefüllt ist, siehe Abbildung 3.1. Für die mathematische Modellierung dieses 

Bauteils werden die folgenden Annahmen getroffen: 

1. Die Berandung des Volumens V ist starr, d.h. das Volumen ist konstant, V = 

konstant. 

2. Die Flüssigkeit innerhalb des Volumens befindet sich in Ruhe, womit im gesamten 

Volumen der gleiche Druck p herrscht. 

3. Das Volumen ist thermisch isoliert und alle thermodynamischen Prozesse sind reversibel. 

Unter diesen Annahmen kann die Flüssigkeit innerhalb des Volumens V durch ein isentropes 

Materialmodell mit einem konstanten Kompressionsmodul β nach Abschnitt 2.3.1 

beschrieben werden, vgl. [1], [2], [10]. Verwendet man die Massenerhaltung in Eulerscher 

Darstellung � � 

∂ 

ρdv = − ρ〈u,n〉da 

∂t V ∂V 

(3.1) 

und beachtet, dass ρ ortsunabhängig ist, so folgt 

V ∂ 

� 

ρ = − ρ〈u,n〉da. 

∂t 

(3.2) 

∂V 

34

3.1 Konstantes hydraulisches Volumen Seite 35 

q1 

q2 

p 

Abbildung 3.1: Konstantes mit Flüssigkeit gefülltes hydraulisches Volumen. 

Des Weiteren wird angenommen, dass das Volumen n Anschlüsse besitzt über die Hydraulikflüssigkeit 

(Öl) zu- bzw. abgeführt werden kann, d.h. es gilt 

� 

− 

∂V 

ρ〈u,n〉da = ρ 

i=1 

V 

qn 

qi 

n� 

� 

− 〈u,n〉da . (3.3) 

� 

∂Vi 

�� 

Darin bezeichnet qi den Volumenstrom des i-ten Anschlusses. Unter Verwendung des Materialgesetzes 

(2.85) folgt dann die Differentialgleichung zur Beschreibung des konstanten 

Volumens in der Form 1 

d β 

p = 

dt V 

qi 

n� 

qi. (3.4) 

Die innerhalb des Volumens gespeicherte innere Energie E ergibt sich aus der spezifischen 

inneren Energie e zu 

E = ρVe = V 

i=1 

� � 

β e p � � 

β −1 −p , (3.5) 

vgl. Aufgabe 2.6. Für die späteren Betrachtungen ist noch die Änderung der inneren 

Energie entlang von Lösungskurven (Trajektorien) des Systems (3.4) von Interesse 

d ∂Edp 

E = 

dt ∂p dt 

= V 

� 

e p 

β −1 

� 

dp 

. (3.6) 

dt 

Durch Einsetzen von (3.4) und unter Verwendung der spezifische Enthalpie h in der Form 

kann folgender Zusammenhang 

gefunden werden. 

h(p) = β 

� 

e 

ρ 

p � 

β −1 = β 

� 

1−e 

ρ0 

d 

E = h(p)ρ 

dt 

n� 

i=1 

qi 

p 

−β � 

, (3.7) 

(3.8) 

1 Da sowohl der Druck p als auch die Dichte ρ ortsunabhängige Größen sind, entspricht die partielle 

Differentiation nach der Zeit t der absoluten Zeitableitung. 

Seminar Regelungstechnik (SS 2011) c○Dr.–Ing. Wolfgang Kemmetmüller 

Institut für Automatisierungs- und Regelungstechnik, TU Wien

3.2 Hydraulische Speicher Seite 36 

Bemerkung 3.1 Offensichtlich ergibt das Produkt der spezifischen Enthalpie h und des 

Massenstroms ˙m = ρ �n i=1qi die dem System zugeführte Leistung. Ein Paar von Systemgrößen 

deren Produkt eine Leistung beschreibt wird auch als kollokiert bezeichnet. Man 

beachte, dass in vielen Standardwerken der Hydraulik das Produkt pq als die dem System 

zugeführte Leistung bezeichnet wird. Diese Näherung ist jedoch nur bei inkompressiblen 

Flüssigkeiten richtig. 

Beispiel 3.1 In diesem Beispiel soll berechnet werden, wieviel Energie in einem hydraulischen 

Volumen V = 1 l bei einem Druck von p = 300 bar gespeichert werden kann. Dazu 

wird angenommen, dass die Hydraulikflüssigkeit den Kompressionsmodul β = 1.6·10 9 Pa 

und eine Dichte ρ0 = 900 kg/m 3 bei Umgebungsdruck p0 = 0 bar aufweist. 

Einfaches Einsetzen in (3.5) liefert 

E = 283J. (3.9) 

Dies ist natürlich ein sehr geringer Wert, insbesondere im Hinblick auf den relativ hohen 

Druck von p = 300 bar. 2 Vergleicht man zusätzlich die Differenz zwischen der Masse m0 

an Flüssigkeit im Volumen bei p = 0 bar mit der Masse m300 bei p = 300 bar, so erhält 

man 

∆m = m300 −m0 = 0.917−0.9 = 0.017kg. (3.10) 

Es kann also nur sehr wenig Hydraulikflüssigkeit in einem konstanten hydraulischen Volumen 

gespeichert werden, womit sich dieses Bauteil nur sehr schlecht als Energie- oder 

Massenspeicher eignet. Die Ursache dafür ist der hohe Kompressionsmodul β von Hydraulikflüssigkeiten. 

3.2 Hydraulische Speicher 

In vielen hydraulischen Anwendungen ist es notwendig hydraulische Energie effizient zu 

speichern. Dies ist unter Anderem zur Stabilisierung von hydraulischen Versorgungen 

oder zur Speicherung von Energie in aktiven Radaufhängungssystemen notwendig. Wie 

das Beispiel 3.1 gezeigt hat, ist ein konstantes hydraulisches Volumen ungeeignet für diese 

Aufgabe. Die Ursache dafür ist der extrem hohe Kompressionsmodul von Hydraulikflüssigkeiten. 

Da Gase einen wesentlich geringeren Kompressionsmodul als Flüssigkeiten besitzen, 

besteht die Grundidee zur Konstruktion eines effizienten hydraulischen Speichers 

in der Kombination von hydraulischen und pneumatischen Teilsystemen. Ein hydraulischer 

Speicher besteht also im Wesentlichen aus einer mit Gas (Stickstoff N2) gefüllten 

Kammer und einer mit Hydraulikflüssigkeit gefüllten Kammer, welche durch einen beweglichen 

Kolben oder eine deformierbare Kunststoffblase getrennt sind. Je nach Ausführung 

werden diese Speicher als Kolben- oder Blasenspeicher bezeichnet. In Abbildung 3.2 ist 

eine Prinzipskizze eines hydraulischen Kolbenspeichers dargestellt. 

2 Die typische Energiedichte (Energie pro Masse) von Lithiumionen-Akkumulatoren bewegt sich im 

Bereich von 300 kJ/kg. 




Nimmt man an, dass das System thermisch isoliert ist und alle thermodynamischen Prozesse 

reversibel sind, so kann das Gas innerhalb des Gasvolumens durch die Adiabatengleichung 

nach Poisson, siehe [11], beschrieben werden 

pgV κ 

g 

Gasvolumen 

Kolben 

Ölvolumen 

= pg0V κ 

g0 = ζ0. (3.11) 

pg 

mp 

po 

Gasanschluss 

qa 

sp,wp 

Ap 

Ölanschluss 

Abbildung 3.2: Prinzipskizze eines Kolbenspeichers. 

Darin bezeichnet pg den Druck und Vg das Volumen des Gases. Die Vorfüllbedingungen 

pg0 und Vg0 sind in der Konstanten ζo zusammengefasst. Der Isentropenkoeffizient κ des 

Gases errechnet sich für ein ideales, zweiatomiges Gas zu 7/5, siehe z.B. [5]. In einem 

realen Gas wie Stickstoff N2 führen die Interaktionen der Moleküle jedoch dazu, dass der 

Isentropenkoeffizient κ mit steigendem Druck p ansteigt und mit steigender Temperatur 

θ abfällt, siehe Abbildung 3.3. 

ImpraktischenBetriebeineshydraulischenSpeicherstretennurrelativgeringeDruck-und 

Temperaturänderungen auf, weswegen eine Approximation mit einem konstanten Isentropenkoeffizienten 

κ zu einer hinreichend genauen Beschreibung des Verhaltens des Gases 

führt. Dieser konstante Wert muss jedoch an den Arbeitsbereich des hydraulischen Speichers 

angepasst werden, vgl. [3]. In Abbildung 3.4 ist ein Vergleich dieser Approximation 

(κ = 2.4) mit der exakten (numerischen) Lösung und dem Verhalten eines idealen Gases 

(κ = 1.4) dargestellt. Man erkennt, dass die Approximation eine sehr gute Näherung des 

realen Verhaltens darstellt, während das ideale Gas (κ = 1.4) nicht zur Beschreibung 

geeignet ist. 

Das aktuelle Volumen Vg des Gases ist durch 

Vg = Apsp, (3.12) 

mit der Kolbenposition sp und der Kolbenfläche Ap gegeben. Unter der Annahme, dass 

die Masse des Gases konstant ist und unter der Verwendung von (3.11) ergibt sich der 

Druck pg zu 

pg = 

ζ0 

(Apsp) κ. (3.13) 



enko 


Druck pg in bar 

Isentropenkoeffizient κ 

460 

440 

420 

400 

380 

360 

340 

320 

300 

280 

3.5 

3.0 

2.5 

2.0 

1.5 

450 bar 

330 bar 

200 bar 

100 bar 

50 bar 

1 bar 

200 300 400 500 600 700 

Temperatur θ in K 

Abbildung 3.3: Isentropenkoeffizient κ für Stickstoff. 

Gasvolumen Vg in l 

Exakte Lösung 

κ = 2.4 

κ = 1.4 

14 14.5 15 15.5 16 16.5 17 

Abbildung 3.4:Volumen des Gases ineinem hydraulischen Speicher: Vergleich der exakten 

LösungmitderLösungunter AnnahmederoptimiertenIsentropengleichung (κ = 2.4)und 

der Isentropengleichung eines idealen Gases (κ = 1.4). 




Das aktuelle Volumen des Öls Vo berechnet sich aus der Differenz des Ölvolumens Va für 

sp = 0 und des Gasvolumens Vg 

Vo = Va −Vg = Va −Apsp. (3.14) 

Schreibt man die Massenerhaltung für das Ölvolumen an und verwendet das Materialgesetz 

einer isentropen Flüssigkeit, so erhält man 3 

d 

dt po = 

β 

Va −Apsp 

(Apwp +qa). (3.15) 

Darin bezeichnet wp = ˙sp die Geschwindigkeit des Kolbens. Das mathematische Modell 

des Kolbenspeichers wird durch die Impulserhaltung des Kolbens 

d 

dt sp = wp 

(3.16a) 

d 

dt wp = 1 

((pg −po)Ap −ff) (3.16b) 

mp 

mit der Masse mp des Kolbens und den auf den Kolben wirkenden Reibungskräften ff 

vervollständigt. 

In vielen Anwendungen sind die Beschleunigungskräfte des Kolbens sehr gering. Des Weiteren 

werden die Dichtungen des Kolbens reibungsoptimiert ausgeführt, sodass auch die 

Reibungskräfte ff vernachlässigbar sind. Damit kann für die Herleitung eines vereinfachten 

Modells des hydraulischen Speichers die Annahme pg = po = pa, mit dem Druck pa 

im Speicher, verwendet werden. Betrachtet man nochmals die Massenerhaltung 

und verwendet 

d 

dt (ρVo) = ρqa 

Vg = 

sowie (3.14), so erhält man das vereinfachte Modell des Kolbenspeichers in der Form 

d 

dt pa = 

� ζ0 

pa 

� 1 

κ 

κβpaqa 

� 

ζ0 κpaVa +(β −κpa) 

pa 

(3.17) 

(3.18) 

� 1 . (3.19) 

κ 

Aufgabe 3.1 Leiten Sie das vereinfachte mathematische Modell aus dem vollständigen 

Modell her. 

3 Zur Beschreibung eines veränderlichen Volumens in welches Masse zu- und abgeführt wird, eignet 

sich weder die Eulersche noch die Lagrangesche Beschreibung der Massenerhaltung. Hier muss eine Kombination 

aus beiden Beschreibungen verwendet werden. 




Alternativ zu einem bewegten Kolben kann auch eine deformierbare Kunststoffblase zur 

Trennung des Öl- und Gasvolumens verwendet werden. Der prinzipielle Aufbau eines solchen 

Blasenspeichers ist in Abbildung 3.5 gegeben. Nimmt man an, dass zur Deformation 

der Kunststoffblase keine Kräfte notwendig sind, dann gilt wie schon beim vereinfachten 

Modell des Kolbenspeichers pg = po = pa. Das mathematische Modell eines Blasenspeichers 

ist daher äquivalent zum vereinfachten Modell eines Kolbenspeichers (3.19). 

Gasvolumen 

Ölvolumen 

pg 

po 

Gasanschluss 

qa 

Blase 

Ölanschluss 

Abbildung 3.5: Prinzipskizze eines Blasenspeichers. 

Für das vereinfachte Modell eines hydraulischen Speichers (3.19) soll nun noch die gespeicherte 

Energie berechnet werden. Die gesamte Energie E eines hydraulischen Speichers 

kann als Summe der Energie Eg des Gasvolumen 

und der Energie Eo des Ölvolumen 

� 

Eo = 

Eg = 

pa 

� ζ0 

pa 

κ−1 

� 1 

κ 

� � � 1 

κ � � 

ζ0 

Va − β e 

pa 

pa � � 

β −1 −pa 

(3.20) 

(3.21) 

berechnet werden, siehe [2], [3]. Die Änderung der gesamten Energie E = Eg+Eo entlang 

einer Lösungskurve des Systems berechnet sich zu 

d 

dt E = h(pa)ρqa, (3.22) 

wobei die spezifische Enthalpie h des Öls durch (3.7) gegeben ist. 

Beispiel 3.2 In diesem Beispiel sollen die Volumina sowie die gespeicherte Energie im 

Öl- und Gasvolumen eines hydraulischen Speichers ermittelt werden. Der betrachtete hydraulische 

Speicher besitzt folgende Daten: 



olumen 


Volumen in l 

• Gesamtvolumen Va = 1 l 

• Isentropenkoeffizient κ = 2 

• Vorfüllbedingungen: Vorfülldruck pg0 = 150 bar, Vorfüllvolumen Vg0 = Va = 1 l, 

Vorfüllbedingung ζ0 = 15 

• Kompressionsmodul des Öls β = 1.6·10 9 Pa 

• Dichte des Öls ρ0 = 900 kg/m 3 

Beim Vorfüllduck pg0 füllt das Gasvolumen den gesamten Speicher aus und somit ist kein 

Öl im Speicher vorhanden, d.h. Vo = 0. Auf der linken Seite der Abbildung 3.6 sind die 

Verläufe des Ölvolumens und des Gasvolumens als Funktion des Druckes pa dargestellt. 

Bei steigendem Druck wird die Gasblase komprimiert und Öl strömt in den Speicher. Mit 

diesem einen Liter großen Speicher können also bei pa = 300 bar ca. 263 g Öl gespeichert 

werden. 

1.0 

0.8 

0.6 

0.4 

Vg 

Druck in bar 

Energie in kJ 

2 

Vo 

0.2 

1 

Eo 

0 

0 

150 200 250 300 150 200 250 300 

7 

6 

5 

4 

3 

Druck in bar 

Abbildung 3.6: Vergleich der Volumina (links) und der Energien (rechts) des Ölvolumens 

und des Gasvolumens eines hydraulischen Speichers. 

Des Weiteren ist auf der rechten Seite von Abbildung 3.6 ein Vergleich der gespeicherten 

Energie im Speicher dargestellt. Man erkennt unmittelbar, dass der bei weitem größte 

Teil der Energie im Gasvolumen gespeichert wird, während nur eine sehr kleine Menge 

von Energie im Öl gespeichert wird. Bei einem Druck von pa = 300 bar kann mit dem 

gewählten Speicher eine Energie von ca. 6.3 kJ gespeichert werden. Vergleicht man dieses 

Ergebnis mit jenem des konstanten hydraulischen Volumens von Beispiel 3.1, so sieht 

man, dass mit einem hydraulischen Speicher eine wesentlich effizientere Speicherung von 

Energie möglich ist. 


Institut für Automatisierungs- und Regelungstechnik, TU Wien 

E 

Eg

3.3 Hydraulikzylinder Seite 42 

3.3 Hydraulikzylinder 

Die Umwandlung von hydraulischer Energie in mechanische (Bewegungs-) Energie ist eine 

wesentliche Aufgabe in elektrohydraulischen Systemen. Das am häufigsten für diese Aufgabenstellung 

verwendete Bauteil ist ein Hydraulikzylinder wie er z.B. in Abbildung 3.7 

dargestellt ist. Dieunterschiedlichen BauformenvonHydraulikzylindern können einerseits 

in einfach bzw. doppelt wirkende Zylinder und andererseits in Einstangen- bzw. Zweistangenzylinder 

unterteilt werden. In der rechten Seite von Abbildung 3.7 ist die Prinzipskizze 

einesdoppeltwirkendenZweistangenzylinders mitunterschiedlichen Kolbenstangendurchmessern 

dargestellt. Obwohl diese Bauform kaum in praktischen Anwendungen eingesetzt 

wird, stellt sie die allgemeinste Bauform dar. Die mathematischen Modelle aller anderen 

Bauformen können sehr einfach vom Modell dieser Bauform abgeleitet werden. 

˙ml1 

sp,wp 

q1 

p1 p2 

Abbildung 3.7: Schnittbild (links) und Prinzipskizze (rechts) eines Hydraulikzylinders. 

Die Massenerhaltung für die Kammer 1 ergibt sich zu 

d 

dt (ρ1(p1)V1) = d 

dt (ρ1(p1)(V01 +A1sp)) = q1ρ1 − ˙ml,1 − ˙ml,12, (3.23) 

mit dem Druck p1, der Dichte ρ1 des Öls in Kammer 1, dem Volumen V1 = V01 + A1sp 

der Kammer 1, der effektiven Kolbenfläche A1, der Position sp des Kolben und dem 

Offsetvolumen V01 der Kammer 1 für sp = 0. Des Weiteren bezeichnet q1 den in die 

Kammer1zufließendenVolumenstromund ˙ml,1 bzw. ˙ml,12 sinddieLeckage-Massenströme 

aus der Kammer 1 in die Umgebung bzw. in die Kammer 2. Verwendet man wiederum 

das Materialgesetz des Öls (2.85), so erhält man die Differentialgleichung des Druckes p1 

in der Kammer 1 

d 

dt p1 = 

β 

V01 +A1sp 

� 

−A1wp − ˙ml,12 

ρ1 

− ˙ml,1 

ρ1 

˙ml12 

q2 

˙ml2 

� 

+q1 , (3.24) 

worin wp = ˙sp die Geschwindigkeit des Kolbens bezeichnet. Auf analoge Art und Weise 

berechnet sich die Differenzialgleichung für den Druck p2 in der Kammer 2 

d 

dt p2 

� 

β 

= A2wp + ˙ml,12 

� 

+q2 , (3.25) 

V02 −A2sp 

ρ2 

− ˙ml,2 

ρ2 

mit der effektiven Kolbenfläche A2, dem Offsetvolumen V02, der Dichte ρ2 sowie dem 

Leckage-Massenstrom ˙ml,2 aus der Kammer 2. 




Die Dichten ρ1 und ρ2 des Öls in der Kammer 1 bzw. Kammer 2 errechnen sich aus (2.86) 

zu 

ρ1 = ρ0e p 1 β und ρ2 = ρ0e p 2 β . (3.26) 

Die durch die Kammerdrücke p1 und p2 erzeugte Druckkraft fp ergibt sich zu 

fp = A1p1 −A2p2, (3.27) 

wobei A1 und A2 wiederum die effektiven Kolbenflächen der Kammern 1 und 2 beschreiben. 

Zusätzlich zur Druckkraft tritt in Hydraulikzylindern immer eine Reibungskraft ff 

auf, welche hauptsächlich von den Dichtungen und der Lagerungen des Kolbens und der 

Kolbenstangen resultiert. Diese Reibung ist in den meisten Fällen eine Kombination aus 

viskoser und Coulombscher Reibung sowie Haftreibung, siehe [7]. Die Größe der Reibung 

ist stark von der Konstruktion des Zylinders abhängig. So werden z.B. die Dichtungen in 

Standardzylindern so ausgelegt, dass keine Leckage auftreten kann. Dazu muss die Dichtung 

sehr fest gegen den Kolben und die Kolbenstange gepresst werden, was in einer 

relativ großen Reibung resultiert. In Anwendungen, die eine hochdynamische Positionierung 

erfordern, werden reibungsoptimierte Zylinder verwendet, welche nur eine sehr 

geringe Coulombsche Reibung und Haftreibung sowie eine kleine viskose Reibung aufweisen. 

In manchen Fällen werden sogar hydrostatisch bzw. hydrodynamisch gelagerte 

Zylinder verwendet, welche keine Haftreibung und eine verschwindend geringe viskose 

Reibung aufweisen. Die Nachteile dieser Konstruktion sind jedoch der wesentlich höhere 

Fertigungsaufwand und die wesentlich erhöhten Leckagen. 

Die Impulserhaltung für den Kolben vervollständigt das mathematische Modell 

mp 

d 

dt sp = wp 

(3.28a) 

d 

dt wp = fp −ff −fl, (3.28b) 

wobei mp die Summe der Masse des Kolbens und aller daran befestigter Komponenten 

beschreibt und fl eine externe Lastkraft ist. 

Die in den beiden Kammern gespeicherte innere Energie E ergibt sich zu E = E1 + E2, 

mit 

� � 

E1 = (V01 +A1sp) β e p � � 

1 

β −1 −p1 

� � 

E2 = (V02 −A2sp) β e 

(3.29a) 

p � � 

2 

β −1 −p2 . (3.29b) 

Des Weiteren ist die kinetische Energie K des Kolbens durch 

K = 1 

2 mpw 2 p 

(3.30) 

gegeben. Die Änderung der Gesamtenergie E+K entlang einer Lösungskurve des Systems 

errechnet sich damit zu 

d 

dt (E+K) = −ffwp −flwp +h(p1)(− ˙ml,12 − ˙ml,1 +ρ1q1)+h(p2)( ˙ml,12 − ˙ml,2 +ρ2q2), 



(3.31)


wobei h(p1) und h(p2) die spezifischen Enthalpien der Flüssigkeit in den Kammern 1 bzw. 

2 beschreiben. Aus (3.31) erkennt man, dass sich die Änderung der Gesamtenergie aus der 

zu- bzw. abgeführten mechanischen Leistung und der zu- bzw. abgeführten hydraulischen 

Leistung zusammensetzt. 

Beispiel 3.3 In diesem Beispiel soll für einen Gleichgangzylinder, d.h. einem Zylinder 

mit A1 = A2 = A, näherungsweise die Schwingungsfrequenz sowie die Laststeifigkeit 

berechnet werden. Dazu wird die Annahme getroffen, dass der Zylinder keine Leckagen 

aufweist und die Volumenströme q1 und q2 verschwinden. Des Weiteren wird die Reibung 

im Zylinder vernachlässigt, d.h. ff = 0. Damit ergeben sich die folgenden Gleichungen 

des mathematischen Modells: 

d 

(3.32a) 

dt sp = wp 

d 

dt wp = 1 

(Ap1 −Ap2 −fl) 

mp 

(3.32b) 

d 

dt p1 

β 

= (−Awp) 

V01 +Asp 

(3.32c) 

d 

dt p2 = 

β 

(Awp). (3.32d) 

V02 −Asp 

Für die weitere Analyse erweist es sich als sinnvoll, die folgende (reguläre) Zustandstransformation 

[sp,wp,p1,p2] T → [sp,wp,fp,pΣ] T , mit der Druckkraft fp = Ap1−Ap2 und dem 

Summendruck pΣ = p1+p2, durchzuführen. Die Gleichungen des transformierten Systems 

ergeben sich zu 

d 

(3.33a) 

dt sp = wp 

d 

dt wp = 1 

(fp −fl) (3.33b) 

mp 

d 

dt fp 

� 2 βA 

= − + 

V01 +Asp 

βA2 

� 

wp (3.33c) 

V02 −Asp 

d 

dt pΣ 

� � 

βA βA 

= − − wp. (3.33d) 

V01 +Asp V02 −Asp 

Man erkennt, dass die ersten drei Gleichungen für die Position sp, die Geschwindigkeit 

wp und die Druckkraft fp nicht vom Summendruck pΣ beeinflusst werden. Daher wird 

in der weiteren Analyse die Differentialgleichung für den Summendruck pΣ nicht weiter 

betrachtet. Unter der Annahme, dass der Zylinder in der Mittelposition steht, d.h. sp = 0, 

und dass der Zylinder symmetrisch ist, d.h. V01 = V02 = V0, sowie für fl = 0 errechnet sich 

die Ruhelage des Systems (3.33a)-(3.33c) zu sp,0 = 0, wp,0 = 0 und fp,0 = 0. Linearisiert 

man das System um diese Ruhelage, so erhält man das linearisierte System in der Form 

⎡ ⎤ ⎡ 

sp 0 1 0 

d 

⎣wp⎦ 

⎢ 1 

= ⎣0 

0 mp 

dt 

fp 0 − 2βA2 

⎤⎡ 

⎤ ⎡ 

sp 0 

⎥ 

⎦⎣wp⎦+ 

⎣− 

0 fp 

V0 

1 

⎤ 

⎦f mp l (3.34a) 

0 

y = sp. (3.34b) 




Nimmt man noch an, dass das Offsetvolumen V0 für sp = 0 durch V0 = AL, mit dem 2 

effektiven Hub L des Zylinders, gegeben ist, dann berechnen sich die Eigenwerte der Dynamikmatrix 

zu 

� 

4βA 

λ1 = 0, λ2,3 = ±I . (3.35) 

Lmp 

� �� 

ω0 

Die Eigenfrequenz ω0 beschreibt dabei die Schwingungsfrequenz des Hydraulikzylinders und 

ist ein Maß für die zur Regelung notwendige Dynamik. 

Die zweite interessante Kenngröße eines Hydraulikzylinders ist die Laststeifigkeit, d.h. die 

Verschiebung sp des Kolbens bei Anlegen einer Lastkraft fl. Diese kann näherungsweise 

aus dem linearisierten Modell über die Beziehung 

fp 

˙ = ∂fp 

∂sp 

berechnet werden. Man beachte, dass der Ausdruck ∂fp 

∂sp 

zweiten Spalte der Dynamikmatrix auftritt und somit zu 

berechnet werden kann. 

∂sp 

∂fp 

� �−1 ∂fp 

= 

∂sp 

wp 

= − L 

4βA 

(3.36) 

bereits in der dritten Zeile und 

(3.37) 

Die Eigenfrequenz sowie die Laststeifigkeit soll nun für einen typischen Hydraulikantrieb 

bestehend aus einem Hydraulikzylinder mit einem Kolbendurchmesser Dk = 40 mm, einem 

Stangendurchmesser Ds = 25 mm, einer Länge L = 200 mm sowie einer Gesamtmasse 

mp = 250 kg, berechnet werden. Der Kompressionsmodul des Öls wird mit β = 1.6 · 10 9 

Pa angenommen. Aus (3.35) folgt die Eigenfrequenz des Systems zu 

und die Laststeifigkeit aus (3.36) ergibt sich zu 

ω0 = 2π49.8 rad/s, (3.38) 

∂sp 

∂fp 

= −4.1·10 −8m 

. (3.39) 

N 

In Abbildung 3.8 ist eine Simulation des nichtlinearen Modells (3.33) für einen Lastkraftsprung 

von 5 kN dargestellt. Man erkennt, dass die Eigenfrequenz und die Laststeifigkeit 

des linearisierten Systems sehr gut mit dem Simulationsergebnis des nichtlinearen Modells 

übereinstimmen. 

3.3.1 Leckagen 

Der typische Strömungspfad von Leckagen ist in Form eines relativ langen und sehr flachen 

Spalts gegeben. Um die Größe und den funktionalen Zusammenhang von Leckage- 

Volumenströmen bzw. Leckage-Massenströmen abzuschätzen, soll die laminare Strömung 




rel. Verschiebung in µm 

50 

0 

−50 

−100 

−150 

175 

150 

p1 

−200 

125 

−250 

−300 

100 

p2 

−350 

−400 

75 

−450 

0 20 40 60 80 100 120 140 160 180 200 

50 

0 20 40 60 80 100 120 140 160 180 200 

t in ms t in ms 

Druck in bar 

Abbildung 3.8: Relative Verschiebung des Kolbens (links) und Kammerdrücke (rechts) für 

eine sprungförmige Lastkraft fl = 5 kN. 

p0 

W 

x 3 

x 1 

x 2 

L 

200 

u1(x 3 ) 

Abbildung 3.9: Prinzipskizze zur Berechnung der Strömung durch einen Flachspalt. 

einer viskosen Flüssigkeit durch einen Flachspalt der Länge L, der Höhe H sowie der 

Weite W berechnet werden, siehe Abbildung 3.9. 

Der Ausgangspunkt der Betrachtungen ist die differentielle Version der Impulserhaltung 

(2.49) mit dem Materialmodell einer viskosen Flüssigkeit (2.87) 

ρ d 

dt u = ρfb +div(σ) (3.40a) 

� 

σ = −pδ +2η d− 1 

3 div(u)δ 

� 

. (3.40b) 

Die allgemeine Darstellung des Geschwindigkeitsvektors u in kartesischen Koordinatenist 

dabei durch 

⎡ ⎤ 

u = ⎣ 

u1 (x1 ,x2 ,x3 ,t) 

u2 (x1 ,x2 ,x3 ,t) 

u3 (x1 ,x2 ,x3 ,t) 

pL 

H 

⎦ (3.41) 

mit den Koordinaten x 1 , x 2 und x 3 sowie der Zeit t, gegeben. Der zugehörige räumliche 




Verzerrungstensor d ergibt sich zu 

⎡ 

⎢ 

d = ⎢ 

⎣ 

1 

2 

1 

2 

∂u1 ∂x1 � 

∂u1 ∂x2 + ∂u2 

∂x1 � 

� 

∂u1 ∂x3 + ∂u3 

∂x1 � 

1 

2 

� 

1 ∂u1 2 ∂x2 + ∂u2 

∂x1 � � 

1 ∂u1 2 

� ∂u 2 

∂u2 ∂x2 ∂x 3 + ∂u3 

∂x 2 

Die Divergenz div(u) ist in kartesischen Koordinaten durch 

div(u) = ∂ua ∂u1 ∂u2 ∂u3 

= + + 

∂xa ∂x1 ∂x2 ∂x3 � 

1 

2 

∂x3 + ∂u3 

∂x1 � 

� 

∂u2 ∂x3 + ∂u3 

∂x2 ⎤ 

� ⎥ 

⎥. 

(3.42) 

⎦ 

∂u 3 

∂x 3 

(3.43) 

gegeben, vgl. (2.35). Damit folgen die Komponenten des Cauchy-Spannungstensors σ für 

eine viskose Flüssigkeit in kartesischen Koordinaten zu 

σ 11 � 

2∂u 

= −p+2η 

3 

1 1∂u 

− 

∂x1 3 

2 1∂u 

− 

∂x2 3 

3 

∂x3 � 

(3.44a) 

σ 22 � 

2∂u 

= −p+2η 

3 

2 1∂u 

− 

∂x2 3 

1 1∂u 

− 

∂x1 3 

3 

∂x3 � 

(3.44b) 

σ 33 � 

2∂u 

= −p+2η 

3 

3 1∂u 

− 

∂x3 3 

1 1∂u 

− 

∂x1 3 

2 

∂x2 � 

(3.44c) 

σ 12 = σ 21 � 

1∂u 

= 2η 

2 

2 1∂u 

+ 

∂x1 2 

1 

∂x2 � 

(3.44d) 

σ 13 = σ 31 � 

1∂u 

= 2η 

2 

3 1∂u 

+ 

∂x1 2 

1 

∂x3 � 

(3.44e) 

σ 23 = σ 32 � 

1∂u 

= 2η 

2 

3 1∂u 

+ 

∂x2 2 

2 

∂x3 � 

. (3.44f) 

Zur Formulierung der Impulserhaltung ist die Berechnung der Divergenz des Spannungstensors 

σ notwendig. Diese berechnet sich (wiederum in kartesischen Koordinaten) zu 

div(σ) 1 = − ∂p 4 

+ 

∂x1 3 η ∂2u1 ∂(x1 ) 2 +η ∂2u1 ∂(x2 ) 2 +η ∂2u1 ∂(x3 ) 

div(σ) 2 = − ∂p 4 

+ 

∂x2 3 η ∂2u2 ∂(x2 ) 2 +η ∂2u2 ∂(x1 ) 2 +η ∂2u2 ∂(x3 ) 

div(σ) 3 = − ∂p 4 

+ 

∂x3 3 η ∂2u3 ∂(x3 ) 2 +η ∂2u3 ∂(x1 ) 2 +η ∂2u3 ∂(x2 ) 

1 

+ 2 3 η ∂2u2 ∂x1 1 

+ 

∂x2 3 η ∂2u3 ∂x1∂x3 (3.45a) 

1 

+ 2 3 η ∂2u1 ∂x1 1 

+ 

∂x2 3 η ∂2u3 ∂x2∂x3 (3.45b) 

1 

+ 

2 3 η ∂2u1 ∂x1 1 

+ 

∂x3 3 η ∂2u2 ∂x2∂x3. (3.45c) 

Schließlich ist die absolute zeitliche Ableitung der Geschwindigkeit du 

durch dt 

d 

dt u1 = ∂u1 

∂t 

d 

dt u2 = ∂u2 

∂t 

+ ∂u1 

∂x 1u1 + ∂u1 

∂x 2u2 + ∂u1 

∂x 3u3 

∂u2 

+ 

∂x1u1 + ∂u2 

∂x2u2 + ∂u2 

∂x3u3 d 

dt u3 = ∂u3 ∂u3 

+ 

∂t ∂x1u1 + ∂u3 

∂x2u2 + ∂u3 

∂x3u3 Seminar Regelungstechnik (SS 2011) c○Dr.–Ing. Wolfgang Kemmetmüller 


(3.46a) 

(3.46b) 

(3.46c)


gegeben. Das aus der Impulserhaltung mit dem Materialgesetz nach (3.40) resultierende 

System von nichtlinearen partiellen Differenzialgleichungen wird in der Literatur als 

Navier-Stokes Gleichungen bezeichnet. Es ist aus der Literatur bekannt, dass eine Lösung 

dieser partiellen Differentialgleichungen in ihrer allgemeinen Form äußerst schwierig 

ist. Daher soll vorerst nur eine stationäre Lösung der Gleichungen gesucht werden. Des 

Weiteren wird angenommen, dass die Flüssigkeit inkompressibel ist. Damit können keine 

Geschwindigkeitskomponenten in x 2 - und x 3 -Richtung auftreten, d.h. 

u 2 = 0, u 3 = 0. (3.47) 

Nimmt man außerdem an, dass der Spalt in Querrichtung unendlich ausgedehnt ist, so 

muss die Geschwindigkeit u1 unabhängig von x2 sein. Schreibt man schließlich noch die 

Massenerhaltung für inkompressible Flüssigkeiten an 

so erhält man 

ρdiv(u) = ρ ∂u1 

= 0, (3.48) 

∂x1 u 1 = u 1 (x 3 ). (3.49) 

Die Impulserhaltung in x 2 - und x 3 -Richtung ergibt sich unter diesen Annahmen zu 

0 = − ∂p 

∂x2 0 = − ∂p 

∂x3, (3.50a) 

(3.50b) 

womit der Druck p nur eine Funktion der x 1 -Koordinate sein kann, p = p(x 1 ). Damit 

verbleibt die Impulserhaltung in x 1 -Richtung 

0 = − ∂p(x1 ) 

∂x1 +η∂2 u1 (x3 ) 

∂(x3 ) 

welche nur gelten kann, wenn der Druck p(x 1 ) die Gleichung 

und die Geschwindigkeit u 1 (x 3 ) die Gleichung 

2 , (3.51) 

∂p(x1 ) 

= C (3.52) 

∂x1 η ∂2u1 (x3 ) 

∂(x3 = C (3.53) 

) 2 

mit einer Konstanten C erfüllen. Löst man die Differentialgleichung (3.52) für den Druck, 

so erhält man mit den Randbedinungen p(0) = p0 und p(L) = pL die Gleichung 

p(x 1 ) = p0 +x 1 P, (3.54) 

mit P = (pL−p0)/L, sowie die Gleichung C = P. Damit kanndie Differentialgleichung für 

die Geschwindigkeit u 1 (x 3 ) mit den beiden Randbedingungen u 1 (0) = 0 und u 1 (H) = 0 

gelöst werden und man erhält den Geschwindigkeitsverlauf 

u 1 (x 3 ) = 1P 

2 η 

� x 3 � x 3 −H �� . (3.55) 




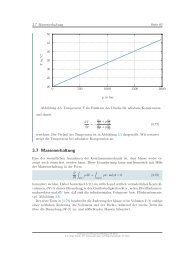
In Abbildung 3.10 ist der Geschwindigkeitsverlauf im Flachspalt für p0 = 100 bar, pL = 0, 

L = 100 mm, H = 0.1 mm sowie η = 35·10 −3 Pas dargestellt. Wie erwartet, ergibt sich 

der für laminare Strömungen charakteristische parabolische Geschwindigkeitsverlauf. 

Geschwindigkeit u1 in m/s 

4 

3 

2 

1 

0 

0 20 40 60 80 100 

Höhe x3 in µm 

Abbildung 3.10: Geschwindigkeitsverlauf u1(x 3 ) in einem Flachspalt. 

ImletztenSchrittmussausderGeschwindigkeit u 1 derVolumen-bzw. Massenstromdurch 

den Flachspalt berechnet werden. Dazu integriert man den Geschwindigkeitsverlauf über 

die Querschnittsfläche Aq des Spaltes 

und erhält 

� 

q = 

Aq 

u 1 (x 3 )da = W 

� H 

x3 u 

=0 

1 (x 3 )dx 3 

(3.56) 

q = 1 H 

12 

3W Lη (p0 −pL). (3.57) 

Der Volumenstrom q einer laminaren Strömung durch einen Flachspalt ist also proportional 

zur Druckdifferenz p0 −pL entlang des Flachspalts. 

Die bisherigen Berechnungen beruhen auf der Annahme einer laminaren Strömung der 

Flüssigkeit durch den Flachspalt. Eine laminare Strömung in einem Flachspalt ist im 

Wesentlichen dadurch gekennzeichnet, dass ein materieller Punkt der Flüssigkeit einer 

gleichmäßigen Bahn, der sogenannten Strömungslinie, folgt, siehe [10]. In diesem Fall 

dominiereninderStrömungdieviskosenKräfte(Zähigkeitskräfte).DieviskoseKraftdichte 

(Kraft pro Fläche) errechnet sich dabei im betrachteten Flachspalt zu 

τv = η ∂u1 

∂x 3. 

(3.58) 

Der laminare Strömungszustand ist jedoch nur bis zu gewissen Strömungsgeschwindigkeiten 

möglich. Bei höheren Strömungsgeschwindigkeiten gewinnt die Trägheitskraftdichte 

τt = ρ(u 1 ) 2 



(3.59)


an Bedeutung und es entstehen Wirbel und Querbewegungen. Durch diese Störbewegung 

wird der Hauptbewegung der Strömung Energie entzogen und es tritt eine sogenannte 

turbulente Strömung auf, vgl. [10]. Als kennzeichnende Größe für den aktuellen Strömungszustand 

(laminar oder turbulent) dient die Reynoldszahl Re, welche sich aus dem 

Verhältnis der Trägheitskraftdichte τt und der viskosen Kraftdichte τv in der Form 

berechnet. Verwendet man die Näherung 

so erhält man 

Re = ρ(u1 ) 2 

η ∂u1 

∂x 3 

∂u 1 

∂x 

3 ≈ u1 

(3.60) 

, (3.61) 

H 

Re ≈ ρu1H . (3.62) 

η 

Für allgemeine Strömungsquerschnitte mit einer charakteristischen Geschwindigkeit u ist 

die Reynoldszahl durch 

Re = ρuDh 

(3.63) 

η 

definiert, wobei Dh den hydraulischen Durchmesser bezeichnet. Er beschreibt das Verhältnis 

der Querschnittsfläche A zum Umfang U eines Strömungsquerschnitts, d.h. 

Dh = 4A 

. (3.64) 

U 

Offensichtlich entspricht der hydraulische Durchmesser Dh für kreisförmige Querschnitte 

demphysikalischenDurchmesserD,währenderfüreinenFlachspaltnäherungsweisedurch 

Dh = 2H, mit der Höhe des Flachspalts H, gegeben ist. Die somit definierte Reynoldszahl 

dient zur quantitativen Abschätzung, ob eine Strömung laminar oder turbulent verläuft. 

Ein typischer Grenzwert für den Übergang von laminarer in turbulente Strömung ist mit 

Re = 2300 für glattwandige, zylindrische Rohre gegeben. Für andere Geometrien der 

Strömungspfade kann dieser Wert wesentlich niedriger sein. 

ImletztenSchritt sollfürdenbetrachtetenFlachspaltuntersucht werden, obdieAnnahme 

einer laminaren Strömung gerechtfertigt war. Für den betrachteten Fall errechnet sich die 

Reynoldszahl mit u = 3.57 m/s zu 

Re = 18.4, (3.65) 

womit die Annahme einer laminaren Strömung mit Sicherheit gerechtfertigt ist. 

Mit den obigen Überlegungen können die Leckage-Massenströme durch 

˙ml,1 = kl,1p1ρ1 

˙ml,2 = kl,2p2ρ2 

(3.66a) 

(3.66b) 

˙ml,12 = kl,12(p1 −p2) ¯ρ12, (3.66c) 

mit den laminaren Leckagekoeffizienten kl,1, kl,2 und kl,12, beschrieben werden. Dabei 

wurde die mittlere Dichte ¯ρ12 = (ρ1 + ρ2)/2 eingeführt, um die Massenerhaltung im 

System zu gewährleisten.

Kapitel 3 Modellierung elektrohydraulischer Bauteile - ACIN

Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.

Template löschen?

Als Template speichern?