und Stammfunktion speziell - K-achilles.de
und Stammfunktion speziell - K-achilles.de
und Stammfunktion speziell - K-achilles.de
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
Integralfunktion <strong>und</strong> <strong>Stammfunktion</strong> bei zusammengesetzten Funktionen (Ac)<br />
Stetigkeit <strong>und</strong> Differenzierbarkeit als Voraussetzung für Integralfunktionen<br />
Die Integralfunktion I a (x) einer Randfunktion f(x) gibt für je<strong>de</strong>s beliebige x das Integral im Intervall<br />
[a ;x] an. (Für positives f(x) ist dies i<strong>de</strong>ntisch mit <strong>de</strong>m Flächeninhalt zwischen G f <strong>und</strong> x-Achse.)<br />
Bei bestimmten Funktionen ist die Integralfunktion bzw. <strong>Stammfunktion</strong> F entwe<strong>de</strong>r schwer zu<br />
bestimmen o<strong>de</strong>r aber sie existiert überhaupt nicht.<br />
Wir betrachten 3 Beispiele:<br />
1. Beispiel: f(x) = ⎢x ⎢=<br />
⎧ x, falls x ≥ 0<br />
⎨<br />
⎩ − x, falls x < 0<br />
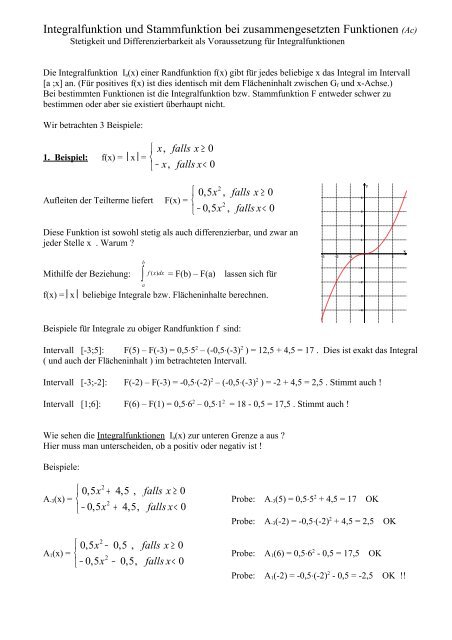
Aufleiten <strong>de</strong>r Teilterme liefert F(x) =<br />
⎧<br />
⎨<br />
⎩ − <<br />
2<br />
0,5 x , falls x ≥ 0<br />
2<br />
0,5 x , falls x 0<br />
4<br />
3<br />
y<br />
Diese Funktion ist sowohl stetig als auch differenzierbar, <strong>und</strong> zwar an<br />
je<strong>de</strong>r Stelle x . Warum ?<br />
2<br />
1<br />
x<br />
-10<br />
-9<br />
-8<br />
-7<br />
-6<br />
-5<br />
-4<br />
-3<br />
-2<br />
-1<br />
1 2<br />
Mithilfe <strong>de</strong>r Beziehung:<br />
f x)<br />
dx<br />
( = F(b) – F(a) lassen sich für<br />
-1<br />
∫ b a<br />
-2<br />
f(x) = ⎢x ⎢ beliebige Integrale bzw. Flächeninhalte berechnen.<br />
-3<br />
-4<br />
Beispiele für Integrale zu obiger Randfunktion f sind:<br />
Intervall [-3;5]:<br />
( <strong>und</strong> auch <strong>de</strong>r Flächeninhalt ) im betrachteten Intervall.<br />
F(5) – F(-3) = 0,5⋅5 2 – (-0,5⋅(-3) 2 ) = 12,5 + 4,5 = 17 . Dies ist exakt -7 das Integral<br />
-5<br />
-6<br />
-8<br />
Intervall [-3;-2]: F(-2) – F(-3) = -0,5⋅(-2) 2 – (-0,5⋅(-3) 2 ) = -2 + 4,5 = 2,5 . Stimmt auch !<br />
Intervall [1;6]: F(6) – F(1) = 0,5⋅6 2 – 0,5⋅1 2 = 18 - 0,5 = 17,5 . Stimmt auch !<br />
Wie sehen die Integralfunktionen I a (x) zur unteren Grenze a aus ?<br />
Hier muss man unterschei<strong>de</strong>n, ob a positiv o<strong>de</strong>r negativ ist !<br />
Beispiele:<br />
A -3 (x) =<br />
A 1 (x) =<br />
⎧ ⎨ + ≥<br />
⎩ − + <<br />
2<br />
0,5x<br />
4,5 , falls x 0<br />
2<br />
0,5x<br />
4,5, falls x 0<br />
⎧ ⎨ − ≥<br />
⎩ − − <<br />
2<br />
0,5x<br />
0,5 , falls x 0<br />
2<br />
0,5x<br />
0,5, falls x 0<br />
Probe: A -3 (5) = 0,5⋅5 2 + 4,5 = 17 OK<br />
Probe: A -3 (-2) = -0,5⋅(-2) 2 + 4,5 = 2,5 OK<br />
Probe: A 1 (6) = 0,5⋅6 2 - 0,5 = 17,5 OK<br />
Probe: A 1 (-2) = -0,5⋅(-2) 2 - 0,5 = -2,5 OK !!
Komplizierter wird die Bestimmung einer <strong>Stammfunktion</strong>, wenn die bei<strong>de</strong>n Funktionsteile von f an<br />
einer Stelle x ≠ 0 zusammenstoßen. Dann muss zuerst eine additive Konstante so bestimmt wer<strong>de</strong>n,<br />
dass Stetigkeit <strong>und</strong> Differenzierbarkeit gewährleistet sind. Daher das<br />
⎧ x, falls x < 1<br />
2. Beispiel: f(x) = ⎨<br />
⎩ 1,5 − 0,5 x, falls x ≥ 1<br />
2<br />
⎧ 0,5 x , falls x < 1<br />
Aufleiten liefert F(x) = ⎨<br />
2<br />
⎩ 1,5 x − 0,25 x + C , falls x ≥ 1<br />
Wählt man nun C = -0,75, so ist F stetig <strong>und</strong> differenzierbar, also eine <strong>Stammfunktion</strong>.<br />
Wegen F(0) = 0 ist mit diesem C = -0,75 eine Integralfunktion zur unteren 0 Grenze gef<strong>und</strong>en.<br />
2<br />
⎧ 0,5 x , falls x < 1<br />
Daher gilt I o (x) = ⎨<br />
2<br />
⎩1,5 x − 0,25x − 0,75, falls x ≥ 1<br />
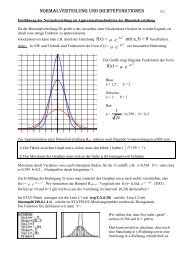
Dieses Beispiel soll nun mit <strong>de</strong>n Möglichkeiten <strong>de</strong>s TI83 untersucht wer<strong>de</strong>n. Dabei wird die Integralfunktion<br />
mittels fnInt(Funktionswert,Variable,untere Grenze,Variable) gezeichnet. Die<br />
Funktionswerte dieser Integralfunktion geben dann das Integral bezüglich <strong>de</strong>r unteren Grenze ( hier 0)<br />
an. Gleichzeitig wer<strong>de</strong>n entsprechen<strong>de</strong> Flächeninhalte zwischen G f <strong>und</strong> x-Achse schraffiert.<br />
Beispiel:<br />
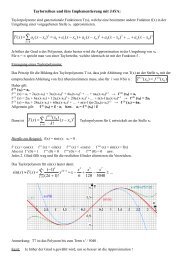
Außer<strong>de</strong>m wird mit TRACE<br />
<strong>und</strong> Wahl von x=4 bei <strong>de</strong>r<br />
I o (4) soll bestimmt wer<strong>de</strong>n: Funktion Y2 das Ergebnis <strong>de</strong>r<br />
Mit CALC 7 wird zunächst eine Integralfunktion ermittelt.<br />
Approximation <strong>de</strong>s Integrals mit Auch hier liefert <strong>de</strong>r Rechner<br />
<strong>de</strong>n Grenzen 0 <strong>und</strong> 4 bestimmt. <strong>de</strong>n Wert 1,25. Dies ist sogar<br />
Der Rechner liefert 1,25. das exakte Ergebnis.<br />
I<br />
Die exakte Rechnung lautet: I o (4) = 1,5⋅4 - 0,25⋅4 2 - 0,75 = 6 – 4 – 0,75 = 1,25 !<br />
Dass zuweilen eine <strong>Stammfunktion</strong> nicht existiert, zeigt das<br />
3. Beispiel:<br />
⎧1, falls x ≥ 0<br />
⎧ x, falls x ≥ 0<br />
f(x) = ⎨<br />
Aufleiten liefert F(x) = ⎨<br />
⎩ 0, falls x < 0<br />
⎩ C , falls x < 0<br />
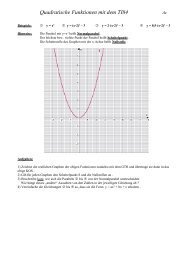
Die erste Bedingung für eine <strong>Stammfunktion</strong> ist die Stetigkeit. Diese erreicht<br />
man bei diesem Beispiel, wenn man C = 0 setzt. Die Funktion ist dann<br />
y<br />
3<br />
2<br />
⎧ x, falls x ≥ 0<br />
1<br />
F(x) = ⎨<br />
. F(x) ist zwar überall stetig, jedoch an <strong>de</strong>r Stelle<br />
⎩ 0, falls x < 0<br />
x = 0 (wo ein Knick auftritt) nicht differenzierbar. Daher ist es keine<br />
-1<br />
<strong>Stammfunktion</strong> ! Aus diesem Gr<strong>und</strong>e lässt sich auch keine Integralfunktion I a angeben.<br />
-12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3<br />
-2<br />
-3<br />
-4<br />
x