Bode-Diagramme (mit Lösung)

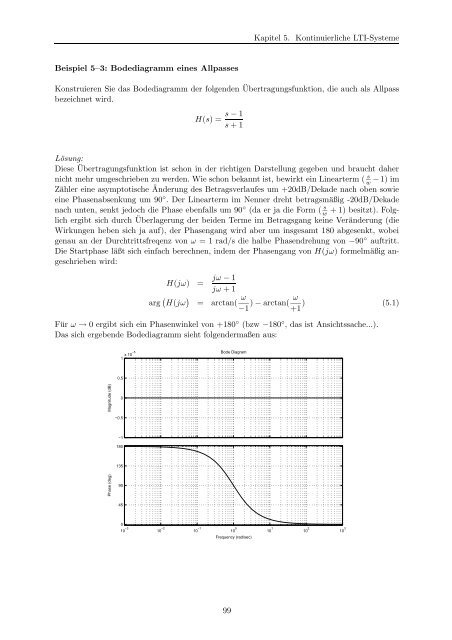
Kapitel 5. Kontinuierliche LTI-SystemeBeispiel 5–3: Bodediagramm eines AllpassesKonstruieren Sie das Bodediagramm der folgenden Übertragungsfunktion, die auch als Allpassbezeichnet wird.H(s) = s − 1s + 1Lösung:Diese Übertragungsfunktion ist schon in der richtigen Darstellung gegeben und braucht dahernicht mehr umgeschrieben zu werden. Wie schon bekannt ist, bewirkt ein Linearterm ( s w− 1) imZähler eine asymptotische Änderung des Betragsverlaufes um +20dB/Dekade nach oben sowieeine Phasenabsenkung um 90 ◦ . Der Linearterm im Nenner dreht betragsmäßig -20dB/Dekadenach unten, senkt jedoch die Phase ebenfalls um 90 ◦ (da er ja die Form ( s w+ 1) besitzt). Folglichergibt sich durch Überlagerung der beiden Terme im Betragsgang keine Veränderung (dieWirkungen heben sich ja auf), der Phasengang wird aber um insgesamt 180 abgesenkt, wobeigenau an der Durchtrittsfreqenz von ω = 1 rad/s die halbe Phasendrehung von −90 ◦ auftritt.Die Startphase läßt sich einfach berechnen, indem der Phasengang von H(jω) formelmäßig angeschriebenwird:H(jω) = jω − 1jω + 1arg ( H(jω ) = arctan( ω −1 ) − arctan( ω +1 ) (5.1)Für ω → 0 ergibt sich ein Phasenwinkel von +180 ◦ (bzw −180 ◦ , das ist Ansichtssache...).Das sich ergebende Bodediagramm sieht folgendermaßen aus:1 x 10−5Bode Diagram0.5Phase (deg) Magnitude (dB)0−0.5−11801359045010 −3 10 −2 10 −1 10 0 10 1 10 2 10 3Frequency (rad/sec)99

Kapitel 5. Kontinuierliche LTI-SystemeBeispiel 5–4: BodediagrammKonstruieren Sie das Bodediagramm der folgenden Übertragungsfunktion.H(s) =s + 10s 212 + 0.1s + 1 3Lösung:Diese Übertragungsfunktion besteht aus einem Linearterm im Zähler und einem quadratischenTerm im Nenner. Zu allererst müssen diese Terme normiert werden:s + 10H(s) =s 212 + 0.1s + 1 310( s10=+ 1)13 ( s2 4+ 0.3s + 1)s10= 30+ 1s 2 4 + 0.3s + 1s10= 30( + 1s) 22 + 2 · 0.3s2 + 1Die interessanten Durchtrittsfreqenzen liegen also bei 2 rad/s und 10 rad/s, die Dämpfung beträgt0.3. Der quadratische Term im Nenner knickt den Betragsgang bei 2 rad/s um 40dB/Dekadenach unten, bei 10 rad/s hebt der Linearterm im Zähler wieder um 20dB/Dekade an, wodurchdie Asymptote für ω → ∞ schlußendlich mit -20dB/Dekade verläuft. Aufgrund der geringenDämpfung ergibt sich an der Knickfrequenz des quadratischen Terms eine Resonanzüberhöhung.Der Phasengang wird vom quadratischen Term bei ω = 2 rad/s um 180 ◦ nach unten gedreht,bei ω = 10 rad/s greift jedoch der positive Linearterm im Zähler, wodurch sich eine Endphasevon −90 ◦ für ω → ∞ ergibt.40Bode Diagram30Phase (deg) Magnitude (dB)20100−10−200−45−90−135−18010 −1 10 0 10 1 10 2Frequency (rad/sec)100

Kapitel 5. Kontinuierliche LTI-SystemeBeispiel 5–5: BodediagrammKonstruieren Sie das Bodediagramm der folgenden Übertragungsfunktion.H(s) =(s + 5)s(s + 2)Lösung:Diese Übertragungsfunktion besteht aus je einem Lineartermen im Zähler und im Nenner, sowieeinem Integrator (Polstelle bei s = 0). Im ersten Schritt wird die Übertragungsfunktion wiedernormiert:(s + 5)H(s) =s(s + 2)5( s 5=+ 1)s · 2( s 2 + 1)= 5 2 · 1 ss · 5 + 1s2 + 1Die interessierenden Knickfrequenzen liegen also bei 2 rad/s und 5 rad/s. Für die erste Betrachtungwird der Integrator weggelassen und das Bodediagramm vonH 1 (s) = 5 2s5 + 1s2 + 1gezeichnet. Mit 20 log 10 V = 20 log 10( 52)≅ 7, 96 hat das Bodediagramm für H1 (s) folgendeGestalt (man beachte, daß die asymptotische Näherung aufgrund der eng beieinanderliegendenKnickfrequenzen 2 rad/s und 5 rad/s in diesem Bereich nur mäßig mit dem hier gezeigtentatsächlichen Bodediagramm übereinstimmt)8Bode Diagram76Phase (deg) Magnitude (dB)5432100−5−10−15−20−25−3010 −2 10 −1 10 0 10 1 10 2 10 3Frequency (rad/sec)101

Kapitel 5. Kontinuierliche LTI-SystemeNun betrachten wir den Integrator separat, d.h die ÜbertragungsfunktionH 2 (s) = 1 s .Bestimmt man Betrags- und Phasengang analytisch,H(s = jω) = 1jω∣∣H(jω) ∣ =1∣jω∣ = |1||jω| = 1 ωoder in dB( ) 120 log 10 = 20 logω10 (1) − 20 log 10 (ω) = −20 log(ω),so ist das Verhalten dieses Termes relativ einfach ersichtlich: ein Integrator erzeugt im Betragsgangeinen konstanten Abfall von 20 dB/Dekade und tritt bei 1 rad/s durch die 0 dB-Linie. Fürden Phasengang giltarg ( H(jω) ) ( ) ( ( )11 0= arg = arctan − arctan = arctan(1) = −jω1)π ω 2 ˆ= − 90◦ .Der Integrator bewirkt also eine Phasendrehung um den konstanten Wert −90 ◦ . Das sieht imBodediagramm folgendermaßen aus:40Bode Diagram20Phase (deg) Magnitude (dB)0−20−40−60−89−89.5−90−90.5−9110 −2 10 −1 10 0 10 1 10 2 10 3Frequency (rad/sec)102