Minimalkostenkombination II-1.pdf - Vorlesungen.info

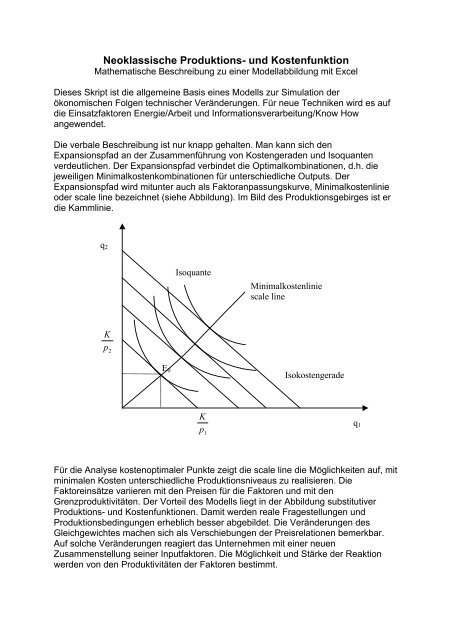
Neoklassische Produktions- und KostenfunktionMathematische Beschreibung zu einer Modellabbildung mit ExcelDieses Skript ist die allgemeine Basis eines Modells zur Simulation derökonomischen Folgen technischer Veränderungen. Für neue Techniken wird es aufdie Einsatzfaktoren Energie/Arbeit und Informationsverarbeitung/Know Howangewendet.Die verbale Beschreibung ist nur knapp gehalten. Man kann sich denExpansionspfad an der Zusammenführung von Kostengeraden und Isoquantenverdeutlichen. Der Expansionspfad verbindet die Optimalkombinationen, d.h. diejeweiligen Minimalkostenkombinationen für unterschiedliche Outputs. DerExpansionspfad wird mitunter auch als Faktoranpassungskurve, Minimalkostenlinieoder scale line bezeichnet (siehe Abbildung). Im Bild des Produktionsgebirges ist erdie Kammlinie.q 2E 0IsoquanteMinimalkostenliniescale lineIsokostengeradeq 1Für die Analyse kostenoptimaler Punkte zeigt die scale line die Möglichkeiten auf, mitminimalen Kosten unterschiedliche Produktionsniveaus zu realisieren. DieFaktoreinsätze variieren mit den Preisen für die Faktoren und mit denGrenzproduktivitäten. Der Vorteil des Modells liegt in der Abbildung substitutiverProduktions- und Kostenfunktionen. Damit werden reale Fragestellungen undProduktionsbedingungen erheblich besser abgebildet. Die Veränderungen desGleichgewichtes machen sich als Verschiebungen der Preisrelationen bemerkbar.Auf solche Veränderungen reagiert das Unternehmen mit einer neuenZusammenstellung seiner Inputfaktoren. Die Möglichkeit und Stärke der Reaktionwerden von den Produktivitäten der Faktoren bestimmt.

Im Excel Modell sind die theoretischen Grundlagen in Beispiele mit konkreten Wertenumgesetzt. Mit dem Modell werden unterschiedliche ökonomische Fragen undAntworten veranschaulicht:- Wie wirken Preisrelationen auf den kostenminimalen Einsatz?- Wie wirken sich Änderungen der Produktivität einzelner Einsatzfaktoren aus?- Was geschieht bei konstanten, sinkenden und steigenden Skalenerträgen?- Die Transaktionskosten werden mit neuen Medien gesenkt. WelcheAuswirkungen hat das auf die Fertigung und die Kostenstruktur?- Wie wird ein natürliches Monopol begünstigt?- usw.Die verwendeten Variablen sind:€€€€p 1,2:= Faktorpreise(Internet : p E:= Arbeit / Energie; p I:= Information)q 1,2:= Faktormengen(Internet : E := Arbeits−,Energieeinsatz;I := Informationsbeschaffung,−verarbeitung)α := Grenzproduktivität − Faktor1β := Grenzproduktivität − Faktor2Die Produktionsfunktion ist vom Typ Cobb-Douglas für zwei variable Einsatzfaktoren:mit a,α,β>0Für einen bestimmten OutputMenge jeweils eines Faktors:1erhält man eine Isoquante durch Auflösen nach der⎛⎛q 2= O ⎞⎞ β0 −⎜⎜ ⎟⎟α q1 β . Die grafische Darstellung sieht man oben. Gesucht wird nun die⎝⎝ a ⎠⎠Faktorkombination mit den geringsten Kosten. Die Kostenfunktion ist einfach dieSumme aus Preisen und Mengen:.Mit einer entsprechenden Auflösung nach der Menge eines Faktors erhält mandaraus:. Die Schnittpunkte mit den Achsen liegen bei und .Eine Minimalkostenkombination, d.h. also eine gegebene Menge, die mit dengeringsten Kosten produziert wird, erhält man als Minimum der Funktionunter der Randbedingung .

Bildet man aus der Randbedingung die implizite Funktion und schreibt dasökonomische Ziel formal, so lautet die Aufgabe:min{ K = p 1q 1+ p 2q 2O 0− aq α 1q β 2≡ 0}€Zur Lösung dieser Aufgabe wenden wir hier die LAGRANGE-Regel an, bei der dieNebenbedingung in die Funktion integriert wird:.Diese Funktion hat eine zusätzliche Variable . Um die notwendige Bedingung fürein Minimum von K zu finden, wird die Funktion nach den jeweiligen Mengen partielldifferenziert:∂K∂q 2= p 2− λaβq 1 α q 2β −1 = 0€Die erste Gleichung kann man auflösen zu:und die zweite zu:. Beide Gleichungen werden verbunden zu:. Multipliziert man beide Seiten der Gleichung mit ,erhält man eine weitere ökonomische Beziehung:umgeformt zu: .Das Verhältnis der Faktoreinsätze entspricht den Preisen, multipliziert mit denjeweiligen Produktivitäten der Faktoren.Die Gleichung aufgelöst nach der Menge ist:

Setzt man die Gleichung für q 1in die obige partielle Ableitung der Kostenfunktionnach ein, so erhält man:€bzw.Daraus folgt dann für die Mengen eine Abhängigkeit von den Preisen, nämlich:Diese Berechnung wird in dem Modell der Excel Tabelle für die Ermittlung despreisabhängigen Faktoreinsatzes verwendet.Des Weiteren ergibt sich aus der Beziehung zwischen Faktoreinsätzen undGrenzproduktivitäten,s.o. ( ) die Berechnung für den zweiten Einsatzfaktor als: .So werden im Excel Modell die preisabhängigen Einsätze der Faktoren berechnet.Die Ergebnisse wurden grafisch umgesetzt. Zu jedem Output erhält man nun denkostenminimalen Input. Im Excel Modell wurde das Ergebnis für jeden Output-Wertberechnet.Für die Produktionsfunktion erhält man durch Einsetzen:, aufgelöst nach ergibt das den allgemeinen Ausdruck, deroben bereits für die Berechnung im Excel Modell zitiert wurde:Unter Verwendung dieser Gleichung und der preisabhängigen Menge fürin die Kostenfunktion erhält man schließlich eine Kostenfunktion, die allein von denPreisen und vom Output abhängig ist:

Diese Kostenfunktion wird im Excel Modell verwendet.Nun können einige Annahmen im Excel Modell variiert und simuliert werden. Solassen sich zum Beispiel die Wirkungen unterschiedlicher Preisentwicklungenberechnen und grafisch darstellen.Die Ergebnisse für sinkende oder steigende Skalenerträge visualisierenEntwicklungen, die zu besonderen Vor- oder Nachteilen im Wettbewerb führen. DieVarianten kann nun jeder mit Inhalten füllen und die Ergebnisse interpretieren.