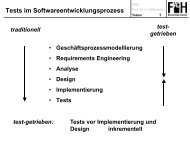
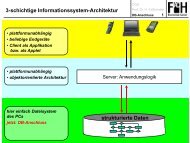
TI12 A82.pdf - FH Aachen

FH Aachen
Fachbereich Elektrotechnik und Informationstechnik
Studiengang Information Systems Engineering (M.Eng.)
Theoretische Informatik
Beweis ungerichteter Hamiltonkreis und
Traveling-Salesman-Problem sind
NP-schwer
Christian Lück, Tobias Neumann, Marcel Stüttgen
Aachen, den 19. Juni 2012

INHALTSVERZEICHNIS
Inhaltsverzeichnis
Inhaltsverzeichnis I
1 Einleitung 1
2 Ungerichteter Hammiltonkreis 2
2.1 Beweis NP-Schwere . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2.2 Beispiel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
3 Traveling-Salesmann-Problem 6
3.1 Beweis NP-Schwere . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3.2 Beispiel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Anhang II
Abbildungsverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . II
- I -

1 Einleitung
1 EINLEITUNG
In dieser Ausarbeitung wird bewiesen, dass sowohl das Problem des ungerichteten Hamiltonkreises
(hamilton circle, HC), als auch das Traveling-Salesman-Problem (TSP) NPschwer
sind.
Hierzu wird im Folgenden zuerst gezeigt, dass sich das Problem des gerichteten Hamiltonkreises
(directed hamilton circle, DHC) in polynomieller Zeit auf das Problem des
ungerichteten Hamiltonkreises (HC) transformieren lässt.
DHC ≤p HC
Anschließend wird eine Transition angegeben, mit der sich das HC-Problem ebenfalls in
polynomieller Zeit auf das Traveling-Salesman-Problem (TSP) transformieren lässt.
HC ≤p T SP
Die folgenden Transformationen sind nicht Bestandteil dieser Ausarbeitung und werden
als gegeben vorrausgesetzt.
SAT ≤p 3KNF -SAT ≤p DHC
Satz 1.0.1 (Satz von Cook). Das SAT Problem ist NP-vollständig.
Satz 1.0.2. Das 3KNF-SAT Problem ist NP-vollständig.
Satz 1.0.3. Das DHC Problem ist NP-vollständig.
Um zu beweisen, dass sowohl HC als auch TSP NP-schwer sind, ist zu zeigen, dass folgende
Aussage gilt.
SAT ≤p 3KNF -SAT ≤p DHC ≤p HC ≤p T SP
- 1 -

2 UNGERICHTETER HAMMILTONKREIS
2 Ungerichteter Hammiltonkreis
Definition 2.0.1 (HC). Gegeben sei ein ungerichteter Graph G = (V, E) mit n Knoten
(n = |V |).
Frage: Existiert in G eine Permutation der Knoten π = � �
vπ(1), vπ(2), . . . , vπ(n) , so dass
für i ∈ {1, 2, . . . , n − 1} gilt:
� � � �
vπ(i), vπ(i+1) ∈ E und vπ(n), vπ(1) ∈ E ?
Anders gefragt: Gibt es in G eine Rundreise, so dass alle Knoten auf der Rundreise in G
genau ein mal enthalten sind?
Satz 2.0.4. HC ist NP-schwer.
2.1 Beweis NP-Schwere
Beweis 2.1.1 (HC ist NP-schwer). Gegeben sei ein gerichteter Graph GDHC = (V, E).
Diese Eingabe wird in polynomieller Zeit in den Graphen GHC umgewandelt, der eine
gültige Eingabe für HC ist, d.h. GDHC ≤p GHC. Dabei werden alle Knoten aus V durch
drei neue Knoten ersetzt. Vorgegangen wird dabei nach folgendem Muster:
.
Zu zeigen ist:
v
(a) Knoten in GDHC
.
.
vin
v
(b) Knoten in GHC
Abbildung 1: Transformation GDHC in GHC
vout
GDHC enthält einen Hamiltonkreis ⇔ GHC enthält einen Hamiltonkreis.
Dazu wird zuerst die Hinrichtung gezeigt:
GDHC enthält einen Hamiltonkreis ⇒ GHC enthält einen Hamiltonkreis.
Ein Hamiltonkreis in GDHC kann in einen Hamiltonkreis in GHC transformiert werden,
indem jeder Knoten v ∈ V (. . . , v, . . . ) durch (. . . , vin, v, vout, . . . ) ersetzt wird.
Um die Äquivalenz zu zeigen, wird nun auch die Rückrichtung gezeigt:
GDHC enthält einen Hamiltonkreis ⇐ GHC enthält einen Hamiltonkreis.
In dem Graphen GHC kann es keinen Hamiltonkreis geben, der einen Knoten vin durchläuft
ohne vorher oder anschließend den Knoten v zu durchlaufen. Genause kann es keinen
Hamiltonkreis geben, der einen Knoten vout durchläuft ohne vorher oder anschließend den
Knoten v zu durchlaufen. Hamiltonkreise in GHC können dadurch in zwei Fälle eingeteilt
werden.
- 2 -
.

2 UNGERICHTETER HAMMILTONKREIS
1. Ein Hamiltonkreis in GHC der einen Knoten durch vin beginnend durchläuft, durchläuft
alle Knoten von vin beginnend.
2. Ein Hamiltonkreis in GHC der einen Knoten durch vout beginnend durchläuft, durchläuft
alle Knoten von vout beginnend. Dieser Hamiltonkreis kann allerdings rückwärts
duchlaufen werden, sodass alle Knoten mit vin beginnend durchlaufen werden.
Es existiert also nur genau dann ein Hamiltonkreis in GHC, wenn auch ein Hamiltonkreis
in GDHC existiert. �
2.2 Beispiel
Betrachten wir zunächst die Hinrichtung:
GDHC enthält einen Hamiltonkreis ⇒ GHC enthält einen Hamiltonkreis.
Hierzu betrachten wir den folgenden gerichteten Graph GDHC:
Abbildung 2: Beispiel gerichteter hamiltonscher Graph
Offensichtlich enthält GDHC einen Hamiltonkreis.
Als nächstes benötigen wir eine äquivalente Darstellung für ungerichtete Hamiltonkreise.
Hierzu ersetzen wir jeden Knoten lokal durch ein 3er-Tupel (siehe Abb. 1). Dabei
werden alle gerichteten eingehenden Kanten des ursprünglichen Knotens zu ungerichteten
Eingängen des 3er-Tupels auf der linken Seite, und alle ausgehenden gerichteten Kanten
des ursprünglichen Knotens zu ungerichteten Ausgängen auf der rechten Seite. Ein Knoten
zählt in dieser Darstellung als ” besucht“, wenn alle drei ” Teilknoten“ des Tupels genau ein
mal durchlaufen werden. Ein Weg π muss das Tupel also entweder von links nach rechts,
oder von rechts nach links vollständig durchlaufen.
- 3 -

2 UNGERICHTETER HAMMILTONKREIS
Wir wenden dieses Transformation auf unseren gerichteten Graphen GDHC an und erhalten
den ungerichteten Graphen GHC:
Abbildung 3: Beispiel ungerichteter hamiltonscher Graph
Wir können nun sowohl ” links-“ als auch ” rechtsherum“ den Graphen durchlaufen und
finden in beiden Fällen einen (ungerichteten) Hamiltonkreis.
Betrachten wir nun die Rückrichtung der Äquivalenz. Wir möchten also zeigen dass gilt:
GDHC enthält einen Hamiltonkreis ⇐ GHC enthält einen Hamiltonkreis.
Diese Aussage ist hingegen äquivalent zu:
GDHC enthält keinen Hamiltonkreis ⇒ GHC enthält keinen Hamiltonkreis.
Um dies zu zeigen, betrachten wir exemplarisch einen neuen Graphen GDHC:
Abbildung 4: Beispiel gerichteter Graph, der nicht hamiltonsch ist
Offensichtlich besitzt unser Graph GDHC keinen gerichteten Hamiltonkreis, da der Knoten
1 von keinem anderen Knoten aus erreichbar ist.
- 4 -

2 UNGERICHTETER HAMMILTONKREIS
Wenden wir unsere Tupel-Transformation (siehe Abb. 1) nun erneut auf den Graphen
GDHC an, so erhalten wir einen veränderten Graphen GHC:
Abbildung 5: Beispiel ungerichteter Graph, der nicht hamiltonsch ist
Startet man nun z.B. vom Knoten 1 aus, so gibt es weder ” links-“ noch ” rechtsherum“
eine Möglichkeit alle Tupel zu durchlaufen.
- 5 -

3 TRAVELING-SALESMANN-PROBLEM
3 Traveling-Salesmann-Problem
Definition 3.0.1 (TSP). Gegeben sei ein vollständiger ungerichteter Graph G = (V, E)
mit n Knoten (n = |V |), eine Funktion c(vπ(i), vπ(j)), die die Kosten der Kante zwischen
den Knoten i und j bestimmt, und eine obere Schranke k.
Frage: Gibt es eine Rundreise π, so dass gilt:
� �
n−1 �
c(vπ(i), vπ(i+1)) + c(vπ(k), vπ(1)) ≤ k ?
i=1
Anders gefragt: Gibt es in G eine Rundreise, deren Kosten ≤ k sind?
Satz 3.0.1. TSP ist NP-schwer.
3.1 Beweis NP-Schwere
Beweis 3.1.1 (TSP ist NP-schwer). Gegeben sei ein ungerichteter Graph GHC = (VHC, EHC)
mit n Knoten, d.h. n = |V |. Diese Eingabe wird in polynomieller Zeit in einen Graphen
GT SP umgewandelt, der eine gültige Eingabe für TSP ist, d.h. HC ≤p T SP . Dabei werden
die Kosten einer Kante gesetzt als (c(i, j) ∈ {0, 1}):
Zu zeigen ist:
�
0 wenn(vi, vj) ∈ EHC
c(i, j) =
1 sonst
GHC enthält einen Hamiltonkreis ⇔ GT SP enthält eine Rundreise mit den Kosten ≤ 0.
Dazu wird zuerst gezeigt:
GHC enthält einen Hamiltonkreis ⇒ GT SP enthält eine Rundreise mit den Kosten ≤ 0.
Sei (v π(1), v π(2), . . . , v π(n), v π(1)) ein Hamiltonkreis in GHC. Alle Kanten, die im Hamiltonkreis
enthalten sind, sind in dem Graphen GHC enthalten. Für i ∈ {1, 2, . . . , n − 1} heißt
das:
(v π(i), v π(i+1)) ∈ EHC und (v π(n), v π(1)) ∈ EHC.
Somit haben alle im Hamiltonkreis enthaltenen Kanten das Gewicht 0, was bedeutet:
c(i, i + 1) = 0 und c(n, 1) = 0.
Dadurch ist die Summe der Gewichte der Kanten ebenfalls 0:
� �
n−1 �
c(i, i + 1) + c(n, 1) = 0
Somit existiert in GT SP eine Rundreise mit den Kosten ≤ 0.
i=1
Um die Äquivalenz zu zeigen, wird nun auch die Rückrichtung gezeigt:
GHC enthält einen Hamiltonkreis ⇐ GT SP enthält eine Rundreise mit den Kosten ≤ 0.
- 6 -

3 TRAVELING-SALESMANN-PROBLEM
Es existiert eine Rundreise in GT SP mit Kosten ≤ 0. Dann ist die Summe der Gewichte
aller in dieser Rundreise enthaltenen Kanten ≤ 0:
� �
n−1 �
c(i, i + 1) + c(n, 1) ≤ 0.
i=1
Da die Kosten der Rundreise ≤ 0 sind und c(i, j) ∈ {0, 1} ist, können nur Kanten mit den
Kosten 0 enthalten sein. Damit sind nur Kanten des Graphen GHC enthalten:
(vi, vi+1) ∈ EHC und (vn, v1) ∈ EHC.
Also ist GHC hamiltonsch. �
3.2 Beispiel
E
D
A
(a) Graph
B
C
E
D
0
A
0
0 0
0
0
0
B
C
(b) Kanten bekommen Gewicht
0
0
E
1
D
0
1
A
0
0 0
0
0
0
B
C
(c) Neue Kanten bekommen
das Gewicht 1
Abbildung 6: Beispiel: Hamilton-Problem zu TSP
- 7 -
0

ABBILDUNGSVERZEICHNIS
Abbildungsverzeichnis
1 Transformation GDHC in GHC . . . . . . . . . . . . . . . . . . . . . . . . . 2
2 Beispiel gerichteter hamiltonscher Graph . . . . . . . . . . . . . . . . . . . . 3
3 Beispiel ungerichteter hamiltonscher Graph . . . . . . . . . . . . . . . . . . 4
4 Beispiel gerichteter Graph, der nicht hamiltonsch ist . . . . . . . . . . . . . 4
5 Beispiel ungerichteter Graph, der nicht hamiltonsch ist . . . . . . . . . . . . 5
6 Beispiel: Hamilton-Problem zu TSP . . . . . . . . . . . . . . . . . . . . . . 7
- II -