Datenstrukturen und Algorithmen Wiederholung Wiederholung Bäume
Datenstrukturen und Algorithmen Wiederholung Wiederholung Bäume
Datenstrukturen und Algorithmen Wiederholung Wiederholung Bäume
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
<strong>Datenstrukturen</strong> <strong>und</strong><br />
<strong>Algorithmen</strong><br />
VO 708.031<br />
09.12.2010 stefan.klampfl@tugraz.at<br />
1<br />
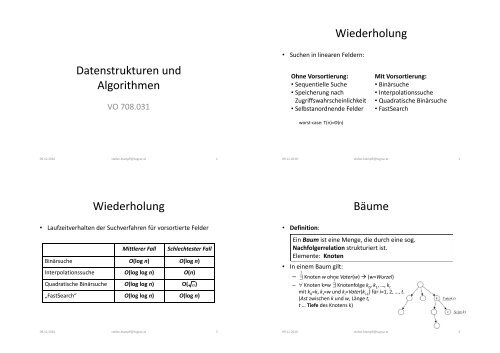
<strong>Wiederholung</strong><br />
• Laufzeitverhalten der Suchverfahren für vorsortierte Felder<br />
Mittlerer Fall Schlechtester Fall<br />
Binärsuche O(log n) O(log n)<br />
Interpolationssuche O(log log n) O(n)<br />
Quadratische Binärsuche O(log log n) O( n)<br />
„FastSearch“ O(log log n) O(log n)<br />
09.12.2010 stefan.klampfl@tugraz.at 3<br />
• Suchen in linearen Feldern:<br />
Ohne Vorsortierung:<br />
• Sequentielle Suche<br />
• Speicherung nach<br />
Zugriffswahrscheinlichkeit<br />
• Selbstanordnende Felder<br />
worst-case: T(n)=Θ(n)<br />
<strong>Wiederholung</strong><br />
Mit Vorsortierung:<br />
• Binärsuche<br />
• Interpolationssuche<br />
• Quadratische Binärsuche<br />
• FastSearch<br />
09.12.2010 stefan.klampfl@tugraz.at 2<br />
• Definition:<br />
<strong>Bäume</strong><br />
Ein Baum ist eine Menge, die durch eine sog.<br />
Nachfolgerrelation strukturiert ist.<br />
Elemente: Knoten<br />
• In einem Baum gilt:<br />
– ∃ Knoten w ohne Vater(w) � (w=Wurzel)<br />
– ∀ Knoten k≠w Knotenfolge k0 , k1 , …, kt mit k0 =k, kt =w <strong>und</strong> ki =Vater(ki-1 ) für i=1, 2, …, t.<br />
(Ast zwischen k <strong>und</strong> w, Länge t,<br />
t … Tiefe des Knotens k)<br />
1<br />
∃ 1<br />
09.12.2010 stefan.klampfl@tugraz.at 4
<strong>Bäume</strong><br />
• Ordnung eines Knotens: Anzahl seiner Söhne<br />
• Ordnung eines Baumes: maximale Ordnung aller Knoten<br />
• Die Knoten eines Baumes sind entweder Blätter (Knoten ohne<br />
Söhne, Ordnung 0) oder innere Knoten (Ordnung >0)<br />
• Jeder Knoten ist Wurzel eines Teilbaumes<br />
• Höhe eines Baumes: Länge des längsten Pfades von der<br />
Wurzel bis zu einem Blatt<br />
• Voller Baum der Ordnung k: Jeder Knoten<br />
hat genau k Söhne oder ist ein Blatt<br />
• Ein vollständiger Baum ist ein voller<br />
Baum, bei dem jedes Blatt gleiche<br />
Tiefe hat<br />
09.12.2010 stefan.klampfl@tugraz.at 5<br />
<strong>Bäume</strong><br />
• Anwendungen in der Informatik:<br />
– Rekursionsbäume<br />
– Entscheidungsbäume<br />
– Suchbäume<br />
– Haldenbäume<br />
– Codebäume u.v.a.<br />
Beispiel (Syntaxbäume):<br />
Arithmetische Ausdrücke<br />
Blätter (= Knoten ohne Söhne) enthalten<br />
Zahlen, innere Knoten speichern<br />
Operatoren (+, -, *, /).<br />
09.12.2010 stefan.klampfl@tugraz.at 7<br />
+<br />
*<br />
2 5<br />
/<br />
+<br />
3 4 3<br />
• Anwendungen:<br />
– Hierarchische Strukturen:<br />
– Inklusionsstrukturen:<br />
<strong>Bäume</strong><br />
09.12.2010 stefan.klampfl@tugraz.at 6<br />
Binärbäume<br />
• Jeder Knoten hat maximal zwei Nachfolger<br />
Existiert ein Sohn- oder ein Vaterknoten nicht,<br />
wird nil zurückgeliefert<br />
09.12.2010 stefan.klampfl@tugraz.at 8
Binärbäume<br />
• Reihenfolge der Knoten:<br />
– Symmetrische Reihenfolge (SR, inorder):<br />
linker Teilbaum in SR, Wurzel, rechter Teilbaum in SR<br />
Beispiel:<br />
+<br />
*<br />
/<br />
+<br />
3 4 3<br />
Aufruf: SR(w)<br />
w … Wurzel<br />
T(n) = Θ(n)<br />
Infix-Notation<br />
2 5<br />
09.12.2010 stefan.klampfl@tugraz.at 9<br />
Sortierte Binärbäume<br />
• Binäre Suchbäume sind in symmetrischer Reihenfolge sortiert<br />
Knoten im linken Teilbaum<br />
≤ Wurzel ≤ Knoten im<br />
rechten Teilbaum<br />
09.12.2010 stefan.klampfl@tugraz.at 11<br />
Binärbäume<br />
• Reihenfolge der Knoten:<br />
– Hauptreihenfolge (HR, preorder):<br />
Wurzel, linker Teilbaum in HR, rechter Teilbaum in HR<br />
– Nebenreihenfolge (NR, postorder):<br />
linker Teilbaum in NR, rechter Teilbaum in NR, Wurzel<br />
+<br />
*<br />
2 5<br />
/<br />
+<br />
3 4 3<br />
Postfix-Notation<br />
(HR)<br />
(NR)<br />
09.12.2010 stefan.klampfl@tugraz.at 10<br />
Sortierte Binärbäume<br />
• Suchen (binäre Suche):<br />
Suchzeit: O(h)<br />
b … gesuchter Wert<br />
k … Wurzel des Teilbaums<br />
Aufruf: SUCHE(b, w)<br />
h … Höhe des Baumes (= Länge des längsten Astes)<br />
09.12.2010 stefan.klampfl@tugraz.at 12
Sortierte Binärbäume<br />
• Minimum <strong>und</strong> Maximum:<br />
k … Wurzel des Teilbaums<br />
Laufzeit:<br />
jeweils O(h)<br />
09.12.2010 stefan.klampfl@tugraz.at 13<br />
Sortierte Binärbäume<br />
• Vorgänger <strong>und</strong> Nachfolger:<br />
Nachfolger von k: was ist der kleinste Wert größer als k?<br />
Laufzeit: O(h)<br />
Wenn ein rechter Sohn<br />
existiert, suche das Minimum<br />
in diesem Teilbaum, …<br />
… sonst suche den niedrigsten<br />
Knoten, bei dem sich k unter<br />
dem linken Sohn befindet<br />
09.12.2010 stefan.klampfl@tugraz.at 15<br />
Sortierte Binärbäume<br />
• Vorgänger <strong>und</strong> Nachfolger:<br />
Vorgänger von k: was ist der größte Wert kleiner als k?<br />
Laufzeit: O(h)<br />
Wenn ein linker Sohn existiert,<br />
suche das Maximum in diesem<br />
Teilbaum, …<br />
… sonst suche den niedrigsten<br />
Knoten, bei dem sich k unter<br />
dem rechten Sohn befindet<br />
09.12.2010 stefan.klampfl@tugraz.at 14<br />
• Einfügen:<br />
Sortierte Binärbäume<br />
Fügt den Wert w in den Binärbaum B ein<br />
Simuliere eine Suche nach w, bis zu einer<br />
freien Stelle (x=nil)<br />
Dort fügen wir das Element ein (als Sohn<br />
von y)<br />
Baum B war leer<br />
Laufzeit: O(h)<br />
09.12.2010 stefan.klampfl@tugraz.at 16
• Entfernen:<br />
Sortierte Binärbäume<br />
Suchen ⇒ Knoten k<br />
a) k ist Blatt: abhängen<br />
b) k hat nur einen Sohn:<br />
Teilbaum von diesem Sohn an VATER(k) anhängen<br />
c) k hat 2 Söhne: Finde den Nachfolger k‚<br />
(k' hat keinen linken Sohn!)<br />
Setze WERT(k) = WERT(k' )<br />
Entferne k'‚ Fall a) oder b)<br />
Laufzeit: O(h)<br />
09.12.2010 stefan.klampfl@tugraz.at 17<br />
• Zusammenfassung:<br />
– Minimum<br />
– Maximum<br />
– Vorgänger<br />
– Nachfolger<br />
– Einfügen<br />
– Löschen<br />
– Suchen<br />
Sortierte Binärbäume<br />
Alle Operationen in O(h) Zeit<br />
h … Baumhöhe<br />
• Vorteil: dynamische Lösung des Wörterbuchproblems<br />
• Nachteil: Zeiten bis zu Θ(n)<br />
09.12.2010 stefan.klampfl@tugraz.at 19<br />
Sortierte Binärbäume<br />
• Aufbau eines sortierten Binärbaumes:<br />
– durch wiederholtes Einfügen (⇒ natürliche <strong>Bäume</strong>)<br />
– Binärbaum hängt von der Reihenfolge der Elemente ab<br />
T(n) = O(n*h)<br />
= Θ(n 2 ), wenn h = Θ(n)<br />
Fügt man randomisiert ein, ist E[h] klein<br />
Einige wenige<br />
Reihenfolgen<br />
liefern entartete<br />
<strong>Bäume</strong> (= Listen)<br />
09.12.2010 stefan.klampfl@tugraz.at 18<br />
Danke für Ihre Aufmerksamkeit!<br />
Bis zum nächsten Mal.<br />
(Donnerstag, 16. Dez. 2010, 11:15, i13)<br />
09.12.2010 stefan.klampfl@tugraz.at 20