Die Eulersche Gerade - Cyril Hertz

Die Eulersche Gerade © 2004 Cyril Hertz
A
u
Feuerbachsche
Neunpunktekreis
H
B‘
D‘
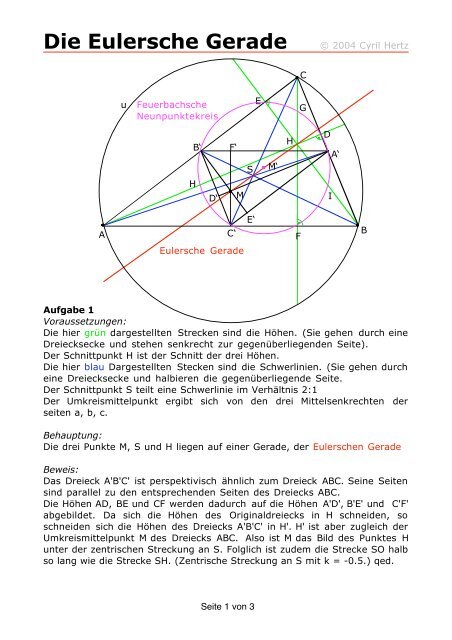
Aufgabe 1
Voraussetzungen:
Die hier grün dargestellten Strecken sind die Höhen. (Sie gehen durch eine
Dreiecksecke und stehen senkrecht zur gegenüberliegenden Seite).
Der Schnittpunkt H ist der Schnitt der drei Höhen.
Die hier blau Dargestellten Stecken sind die Schwerlinien. (Sie gehen durch
eine Dreiecksecke und halbieren die gegenüberliegende Seite.
Der Schnittpunkt S teilt eine Schwerlinie im Verhältnis 2:1
Der Umkreismittelpunkt ergibt sich von den drei Mittelsenkrechten der
seiten a, b, c.
Behauptung:
Die drei Punkte M, S und H liegen auf einer Gerade, der Eulerschen Gerade
Beweis:
Das Dreieck A'B'C' ist perspektivisch ähnlich zum Dreieck ABC. Seine Seiten
sind parallel zu den entsprechenden Seiten des Dreiecks ABC.
Die Höhen AD, BE und CF werden dadurch auf die Höhen A'D', B'E' und C'F'
abgebildet. Da sich die Höhen des Originaldreiecks in H schneiden, so
schneiden sich die Höhen des Dreiecks A'B'C' in H'. H' ist aber zugleich der
Umkreismittelpunkt M des Dreiecks ABC. Also ist M das Bild des Punktes H
unter der zentrischen Streckung an S. Folglich ist zudem die Strecke SO halb
so lang wie die Strecke SH. (Zentrische Streckung an S mit k = -0.5.) qed.
F‘
C‘
M
Eulersche Gerade
S
E‘
Seite 1 von 3
E
M‘
H
F
C
G
D
I
A‘
B

Die Eulersche Gerade © 2004 Cyril Hertz
Ergänzungen zur Aufgabe 1
- Wenn das Dreieck ABC gleichseitig ist, fallen die Schwerlinien mit der Höhe
und dem Umkreismittelpunkt zusammen und es kann keine Eulersche
gerade festgestellt werden. (sie fällt zusammen zu einem Punkt).
- Wenn das Dreieck ABC möglichst ungleichseitig ist, wird die Eulersche
Gerade „genauer“, weil die Punkte weiter auseinander liegen.
- Wenn das Dreieck ABC bei der Ecke A rechtwinklig ist, fallen D, H und E mit
A, und E‘, M und F‘ mit A‘ zusammen.
- Wenn das Dreieck ABC bei der Ecke B rechtwinklig ist, fallen F, H und D mit
B, und F‘, D‘ und B‘ mit M zusammen.
- Wenn das Dreieck ABC bei der Ecke C rechtwinklig ist, fallen E, H und D mit
C, und D‘, M und E‘ mit C‘ zusammen.
Aufgabe 2
Der Punkt S liegt auf der Eulerschen Gerade und wird abgebildet auf den
Punkt S‘, der auf der Eulerschen geraden zu liegen kommt. Demzufolge
muss der Punkt M, der ebenfalls auf der Eulerschen Gerade liegt, auf sie
abgebildet werden. (Bei der Zentrischen Streckung wird keine Gerade
verkrümmt) qed.
Aufgabe 3
Behauptung:
S und H sind Streckungszentren der beiden Kreisen M und M‘.
Beweis für S:
Dreieck C‘A‘S ist perspektiv ähnlich zum Dreieck CAS
Da Teilverhältnisse erhalten bleiben gilt:
B‘S : C‘S = SC : SB qed.
Beweis für H:
Dreieck HBR ist perspektiv ähnlich zum Dreieck HEC
Da Teilverhältnisse erhalten bleiben gilt:
HB : HF = HC : HE qed.
Aufgabe 4
S‘
Behauptung:
Wenn man das Dreieck A‘B‘C‘ perspektivisch
ähnlich abbildet, werden Die Punkte auf die
A‘
A
C‘‘‘‘‘
S
C‘‘‘
B‘
B
Eckpunkte zu liegen kommen.
A‘‘‘‘‘
Es müssen somit die
• drei Höhenfusspunkte (D, E, F) X = X‘
• drei Mittelpunkte A‘, B‘, C‘ der Seiten und
• drei Mittelpunkte G, H, I der bei den
Ecken liegenden Höhenabschnitte
S‘‘‘
B‘‘‘‘‘
A‘‘‘
Y = Y‘
B‘‘‘‘
B‘‘‘
Z = Z‘
A‘‘‘‘
S‘‘‘‘
auf einem Kreis liegen (Feuerbachschen Neunpunktekreis)
C‘‘‘‘
Seite 2 von 3
C‘
C

Die Eulersche Gerade © 2004 Cyril Hertz
Beweis:
J
A
u
Feuerbachsche
Neunpunktekreis
JE : JH = BI : BH = KD : KH = 1:2
A‘S : SA = B‘S : SB = C‘S : SC = 1:2
daraus folgt:
HI = IB, HH‘ = H‘A, HG = GC qed.
B‘
H‘
D‘
F‘
C‘
Kommentar:
Die Nummer 4 fand ich eher kompliziert, da ich mühe hatte, den
Beweisansatz herauszufinden. Allgemein waren die Beweise das
schwierigste. Meine Zeichnung wirkt vielleicht ein wenig „überladen“.
Vielleicht hätte ich besser zwei Figuren aufgezeichnet, dann wäre die
Übersicht gewährleistet. Da ich aber bei den Aufgaben fast immer die ganze
Figur brauchte, nahm ich sie nicht auseinander.
M
Eulersche Gerade
S
E‘
E
Seite 3 von 3
M‘
H
F
C
G
L
D
I
A‘
K
B