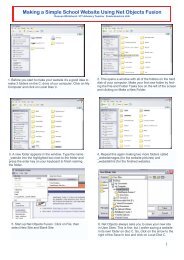
Polyhedra – Mathematical process It is important that the children ...

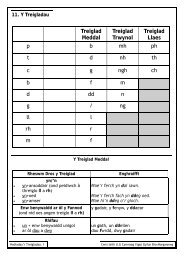
• Number of vertices
This could be tackled by looking at the table of results
Shape Number of
edges
Cube
Number of
faces
Number of
vertices
12 6 8
Triangular
prism 9 5 6
Hexagonal
prism 18 8 12
It could also be tackled by rearranging the formula
(f + v) – 2 = e
v – 2 = e ­ f (taking f away from both sides)
v = e + f + 2 (adding 2 to both sides)
Our general term is v = (e ­ f) + 2
Problem 2
­
+ 2 =
Process/Strategy
They should notice
that the number of
vertices can be
found by taking the
number of faces
away from the
number of edges
and adding 2.
• Be systematic
NB It should be noted that these results are based on the use of the 3D shapes
that can be constructed from the nets within the pack. The results will vary if you
use different 3D shapes (e.g. our pentagonal prism is made up of pentagons and
squares. You may have a pentagonal prism that is made up of pentagons and
rectangles.)
Each of the 3D shapes needs to be studied and the name of the different 2D
shapes that make up its faces need to be recorded. The children could use the
interactive program to study the shapes or the nets of the shapes can be printed
out and constructed.
5
4 3
1
1
2
Pentagonal based pyramid is made up of 5 triangles
and 1 pentagon.