7.4 - Sum and Difference Identities

7.4 - Sum and Difference Identities
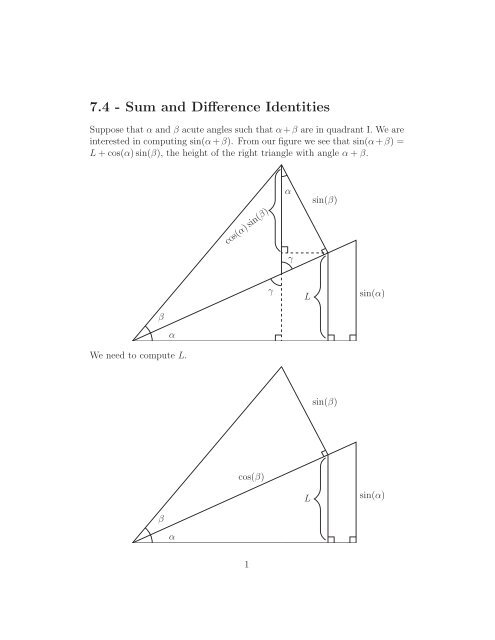
Suppose that α and β acute angles such that α+β are in quadrant I. We are
interested in computing sin(α+β). From our figure we see that sin(α+β) =
L+cos(α)sin(β), the height of the right triangle with angle α+β.
β
α
We need to compute L.
β
α
cos(α)sin(β)
cos(β)
1
γ
α
γ
L
L
sin(β)
sin(β)
sin(α)
sin(α)

L
Bysimilartrianglesweseethat
Hence we have
sin(α)
= cos(β)
1 andthereforeL = sin(α)cos(β).
sin(α+β) = cos(α)sin(β)+sin(α)cos(β).
Sum and Difference Identities
We have established the following result.
Theorem 1.
cos(a±b) = cos(a)cos(b)∓sin(a)sin(b)
sin(a±b) = sin(a)cos(b)±cos(a)sin(b)
tan(a±b) = tan(a)±tan(b)
1∓tan(a)tan(b)
Example 1. Findcos(α+β),giventhatαandβ areinquadrantIII,cos(α) =
−3 12 , and tan(β) = 5 5 .
We have cos(α) = − 3
5
−12
−3
−4
α
5
−5
13
5
, sin(α) = −4,
cos(β) = − 5 13
cos(α+β) = cos(α)cos(β)−sin(α)sin(β) =
β
− 3
5
− 5
13
and sin(β) = −12
13 ,
− − 4
−
5
12
13
Example 2. Use a trig formula to find the exact value for the expression
tan
π . 12
2
.

We have
Example 3. Verify
We have
π
π
tan = tan
12 3
= tan π
3
=
π
−
4
π −tan 4
1+tan
π π
tan 3 4
√
3−1
1+ √ 3 .
sin(x+y) tan(x)+tan(y)
=
sin(x−y) tan(x)−tan(y) .
sin(x+y) sin(x)cos(y)+sin(y)cos(x)
=
sin(x−y) sin(x)cos(y)−sin(y)cos(x)
=
=
sin(x)cos(y)+sin(y)cos(x)
cos(x)cos(y)
sin(x)cos(y)−sin(y)cos(x)
cos(x)cos(y)
sin(x)
cos(x)
+ sin(y)
cos(y)
sin(x) sin(y)
− cos(x) cos(y)
= tan(x)+tan(y)
tan(x)−tan(y) .
Example 4. Show that cos(x+2π) = cos(x).
By the angle addition formula we get
cos(x+2π) = cos(x)cos(2π)−sin(x)sin(2π) = cos(x).
Co-Function Identities
The co-function identities are given by
π
sin
2 −x
π
= cos(x) cos
2 −x
π
= sin(x) tan
2 −x
= cot(x)
π
csc
2 −x
π
= sec(x) sec
2 −x
π
= csc(x) cot
2 −x
= tan(x).
3

Example 5. Express csc( π
2
−x) in term of sec.
π
csc
2 −x
= sec(x).
Example 6. Express sin(3x) in terms of cos.
π
sin(3x) = cos
2 −3x
.
Example 7. Find
x−2
cos arctan .
x
Now
tan(θ) = x−2
x
implies that the hypotenuse of the triangle is x2 +(x−2) 2 .
Therefore cos(θ) =
An Application
x−2
√ x
x2 +(x−2) 2 .
x 2 +(x−2) 2
x
Example 8. Sound is a result of waves applying pressure to a person’s
eardrum. Foraparticularwaveradiatingoutward, thetrigonometricfunction
P(r) = a cos(πr−1000t) can be used to express pressure at a radius of r feet
r
from the source after t seconds. In this formula, a is the maximum sound
pressure at the source, measured in pounds per square foot.
Use a difference identity to simplify the expression for P(r) when r is an
even integer.
We get
cos(rπ −1000t) = cos(rπ)cos(1000t)+sin(rπ)sin(1000t)
and if r is even we have rπ = 0,2π,4π,... and therefore
cos(2kπ−1000t) = cos(1000t).
4
θ

Extra problems
1. If a person with weight W bends at the waist with a straight back, then
the force F exerted by the lower back muscles may be approximated
using F = 2.89W sin(θ+90 ◦ ), where θ is the angle between a person’s
torso and the horizontal. Approximate the value of θ that will cause a
130 pound person’s back muscles to exert a force of 200 pounds.
2. Given cos(s) = − 15
and cos(t) = −4,
and that s and t are in quadrant
17 5
II, find sin(s+t),cos(s+t),tan(s+t) and the quadrant of s+t.
3. Find the angle of intersection, θ, for lines l1 and l2 if their slopes are
given by tan(α) and tan(β) and show that θ satisfies the following,
where α and β are acute angles.
Khan Academy Video Links
Proof of sin(a+b)
Proof of cos(a+b)
tan(θ) = tan(β)−tan(α)
1+tan(α)tan(β)
5