Math 1300 Written Homework #10 Solutions 4.2, Q. 24. Let y = at 2e ...

Math 1300 Written Homework #10 Solutions
4.2, Q. 24. Let y = at 2 e −bt with a and b positive constants. For t ≥ 0, what value of t maximizes y?
Sketch the curve if a = 1 and b = 1.
Solution: Compute the derivative: we get
y ′ (t) = (at 2 )(−be −bt ) + (2at)(e −bt ) = at(−bt + 2)e −bt .
There are two critical points, at t = 0 and t = 2
b .
To find the global maximum, we look at the critical points and the behavior as y approaches
the endpoints. In this case t = 0 is both a critical point and an endpoint, while the limit as
t → ∞ is the other “endpoint.” So the global maximum is whichever of
is the largest.
f(0), f(2/b), lim
t→∞ f(t)
It is easy to see that f(0) = 0 and lim
t→∞ f(t) = 0 (since f(t) = (at 2 )/(e bt ) and any exponential
dominates any power as t → ∞). So if f(2/b) is positive, it must be the maximum.
We compute
f
2
=
b
4a
b2 e−1 ,
which is indeed positive, so t = 2
is the global maximum.
b
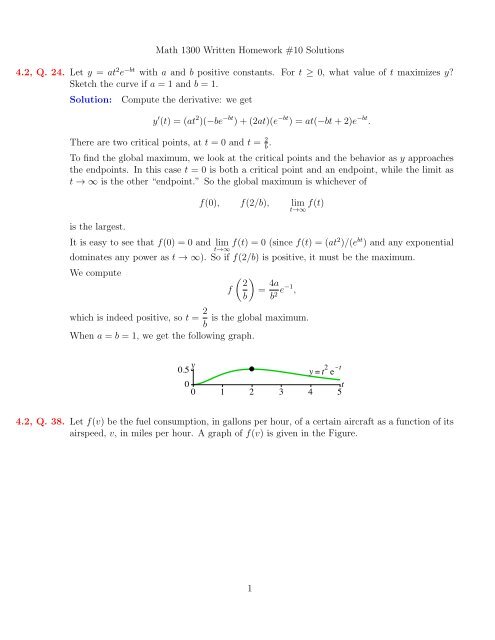
When a = b = 1, we get the following graph.
4.2, Q. 38. Let f(v) be the fuel consumption, in gallons per hour, of a certain aircraft as a function of its
airspeed, v, in miles per hour. A graph of f(v) is given in the Figure.
1

a. Let g(v) be the fuel consumption of the same aircraft, but measured in gallons per mile
instead of gallons per hour. What is the relationship between f(v) and g(v)?
Solution: Suppose v = 100 miles per hour; then from the graph, f(100) = 50 gallons
per hour. So in the next one hour, the aircraft will travel about 100 miles and use up
about 50 gallons of fuel. Assuming the speed and fuel consumption stay constant over
that hour, the plane is using 50 1 = gallons of fuel per mile traveled.
100 2
More generally,
g(v) = = f(v) gallons
v mile .
f(v) gallons
hour
v miles
hour
Notice how the units “gallons per hour” divided by the units “miles per hour” cancels out
to give “gallons per mile,” which are the units we were supposed to get. Units confirm
that we are thinking about the problem in the right way.
b. For what value of v is f(v) minimized?
Solution: We just want the critical point, where f ′ (v) = 0. This seems to occur around
v = 220 miles per hour.
c. For what value of v is g(v) minimized?
Solution: g(v) will have the same general shape as f(v), with a vertical asymptote at
v = 0 and increasing toward infinity as v goes to infinity. So we just need the critical
point of g(v).
Using the Quotient Rule, we get
g ′ (v) = d
dv
f(v)
v
= vf ′ (v) − f(v)
v2 .
The critical point we care about is wherever f(v) = vf ′ (v). The best way to see this
from the graph is to notice that geometrically, we will have
f(v)
v = f ′ (v)
2

when the line from the origin to (v, f(v)) coincides with the tangent line at (v, f(v)).
(Or in other words, when the tangent line to the graph passes through the origin.)
From the graph this seems to happen when v ≈ 300 miles per hour.
d. Should a pilot try to minimize f(v) or g(v)?
Solution: Presumably the pilot intends to go the same speed for almost the entire trip,
which means f(v) and g(v) will both be constants for the pilot. That means the total
fuel used will be either f(v) times the number of hours the trip takes, or g(v) times the
number of miles the trip takes.
Now the number of hours the trip takes depends on the speed (so it’s not constant!), but
the number of miles the trip takes is the same no matter what the speed is. So I would
expect that a pilot wants to minimize g(v), the fuel used per mile traveled.
3

4.2, Q. 40. The Figure gives the derivative of g(x) on −2 ≤ x ≤ 2.
a. Write a few sentences describing the behavior of g(x) on this interval.
Solution: First of all, g ′ (x) is always less than or equal to zero. That means the
original function g(x) is always decreasing on the interval [−2, 2]. Furthermore g ′ (x) is
decreasing from −2 to 0, then increases from 0 to 2. That means g(x) is concave down
from −2 to 0 and concave up from 0 to 2.
b. Does the graph of g(x) have any inflection points? If so, give the approximate xcoordinates
of their locations. Explain your reasoning.
Solution: The inflection point of g(x) is at x = 0, where it changes concavity.
It is possible that x = −2 and x = 2 would also be inflection points of the full graph, but
they do not count here since the function does not actually change concavity at x = 2:
g ′ (x) doesn’t even seem to exist for x > 2, and even if it did, we have no idea whether
g ′ (x) decreases or increases for x > 2.
c. What are the global maxima and minima of g on [−2, 2]?
Solution: The global maximum of g(x) occurs at x = −2, since g(x) is decreasing from
−2 to 2. Similarly the global maximum occurs at x = 2.
d. If g(−2) = 5, what do you know about g(0) and g(2)? Explain.
Solution: I know that g(0) is smaller than 5 and that g(2) is even smaller than g(0).
There are no vertical units on the graph, so there is no way of knowing just how much
smaller g(0) is.
The one thing you could say is that
g(2) − g(0) = g(0) − g(−2),
or in other words that g(2) = 2g(0) − 5. The reason for this is basically that g(x) is not
necessarily an odd function, but since its derivative is even, it has to be a vertical shift
of an odd function. That means the secant line from −2 to 0 must have the same slope
as the secant line from 0 to 2. This is a bit more sophisticated though.
4.3, Q. 39. a. Find all critical points of f(x) = x 4 + ax 2 + b.
Solution: The derivative is
f ′ (x) = 4x 3 + 2ax.
This always exists, so to find critical points we set it to zero.
4x 3 + 2ax = 0
2x(2x 2 + a) = 0.
4

We see that x = 0 is always a critical point. Whether there are other critical points
depends on the sign of a. If a < 0 then x = ± (−a/2) are the two other critical points
(and so there are three). If a = 0 then we just get x = 0 again (so there is only one).
Finally if a > 0 then we get no additional critical points (so there is just the one at
x = 0).
b. Under what conditions on a and b does this function have exactly one critical point?
What is the one critical point, and is it a local maximum, a local minimum, or neither?
Solution: It has exactly one critical point when a ≥ 0. In this case x = 0 is the one
critical point. To test whether it is a local maximum or local minimum, we plug in values
to the left and right. For example when x = −1 we get f ′ (−1) = −2(2 + a) which is
negative since a ≥ 0. Similarly f ′ (1) = 2(2 + a) > 0. So the function is going from
decreasing to increasing, and thus x = 0 is a local minimum.
c. Under what conditions on a and b does this function have exactly three critical points?
What are they? Which are local maxima and which are local minima?
Solution: It has exactly three critical points if a < 0. They are x = 0, x = − (−a/2),
and x = (−a/2). To see which are local maxima and which are local minima, we use
the second derivative test. We have f ′′ (x) = 12x 2 + 2a, so that
f ′′ (0) = 2a, f ′′ (− (−a/2)) = −4a, f ′′ ( (−a/2)) = −4a.
Now a < 0, so that means f ′′ is negative at x = 0 and positive at the two other critical
points. That means x = 0 is a local maximum and x = ± (−a/2) are both local
minima.
d. Is it ever possible for this function to have two critical points? No critical points? More
than three critical points? Give an explanation in each case.
Solution: None of these things are ever possible. The derivative is of the form 2x(2x 2 +
a). So it either has one root or three roots, depending on whether 2x 2 + a can ever be
zero. And if 2x 2 + a can be zero, it must be zero twice (since the negative of any root is
also a root).
5

4.3, Q. 50. Consider the family
y = A
x + B .
a. If B = 0, what is the effect of varying A on the graph?
Solution: We have the family y = A
. Varying A corresponds to rescaling the y-values
x
of the graph, so increasing A will stretch the graph vertically. It will still have the same
basic shape (vertical asymptote at x = 0, horizontal asymptote at y = 0).
b. If A = 1, what is the effect of varying B?
Solution: We have the family y = 1
, which has a vertical asymptote at x = −B.
x + B
Varying B moves this vertical asymptote, but does not change the shape of the graph.
c. On one set of axes, graph the function for several values of A and B.
Solution: Here I have graphed: A = 1, B = 1 in red, A = 2, B = 1 in blue, A = 1,
B = −2 in yellow, and A = −1, B = −2 in green.
4.3, Q. 54. For positive A, B, the force between two atoms is a function of the distance, r, between them:
f(r) = − A B
+
r2 r3 r > 0
a. What are the zeros and asymptotes of f?
Solution: It’s easier to answer this by getting a common denominator:
f(r) =
B − Ar
r3 .
This is zero when r = B/A, and it has a vertical asymptote when r = 0. It has a
horizontal asymptote at y = 0.
6

. Find the coordinates of the critical points and inflection points of f.
Solution: To take the derivative, we write f(r) = −Ar −2 + Br −3 so we can use the
Power Rule. We get
and
f ′ (r) = 2Ar −3 − 3Br −4 =
f ′′ (r) = −6Ar −4 + 12Br −5 =
2Ar − 3B
r 4
12B − 6Ar
r5 .
The critical points are r = 0 and r = 3B
2B
. The inflection points are r = 0 and r =
2A A .
c. Graph f.
Solution: Here it is, with the zero, the minimum, and the inflection point labeled.
d. Illustrating your answers with a sketch, describe the effect on the graph of f of:
(a) Increasing B, holding A fixed
(b) Increasing A, holding B fixed
Solution: The fact that our three interesting x values occur at multiples of B/A means
that increasing B moves those points to the right, and increasing A moves those points
to the left. More subtly, the y-value at the minimum can be computed: plug in r = 3B
2A
to the formula to get f( 3B 4A3 ) = − 2A 27B2 . Thus increasing B will shrink that minimum value
toward the x-axis, while increasing A will move it away from the x-axis.
4.4, Q. 24. Find the minimal and maximal value of x in Figure 4.54.
Solution: 0 ≤ x ≤ 10, so the minimum is 0 and the maximum 10.
4.4, Q. 38. The cross-section of a tunnel is a rectangle of height h surmounted by a semicircular roof
section of radius r (see figure 4.56). If the cross-sectional area is A, determine the dimensions
of the cross section which minimize the perimeter.
7

Solution: The perimeter P = 2r+2h+πr (the bottom, plus the 2 sides, plus the semicircular
arc on top). The area A = 2rh + πr 2 /2 is fixed, so we can solve that h = (A − πr 2 /2)/2r,
getting that
P = r(2 + π) + 2(A − πr 2 /2)/2r = r(2 + π/2) + A/r,
where r > 0 and r < 2A/π (so h > 0). We find critical points by differentiating P
with respect to r, yielding dP
dR = 2 + π/2 − A/r2 , which exists since r > 0, and is 0 when
r2 = A/(2 + π/2), so r = A/(2 + π/2). Since there is precisely 1 critical point, and the
derivative is negative for r < A/(2 + π/2) and positive for r > A/(2 + π/2), we have
that r = A/(2 + π/2) produces the minimum perimeter, and
h = (A − πA/(4 + π))/2 A/(2 + π/2) = √ A/(2 + π/2) 3/2 .
4.4, Q. 40. Of all rectangles with given area, A, which has the shortest diagonals?
Solution: Say the rectangle is x by y, so xy = A. Then the diagonal length we want to
mimimize is x 2 + y 2 . This is the same as minimizing s = x 2 + y 2 , which is much easier to
handle algebraically. Since y = A/x, we have
s = x 2 + A 2 /x 2 ,
where x > 0. We compute ds
dx = 2x − 2A2 /x 3 , which exists everywhere, and is zero when
x 4 = A 2 , so x = √ A. Since the derivative is negative for x < √ A and positive for x > √ A,
this is a minimum. Note that y = A/ √ A = √ A. So the square has the shortest diagonals for
a given area.
8