Math 1300 Fall 2012 Exam #3 Solutions 1. Multiple Choice. (a ...

1. Multiple Choice.
x
(a) Compute lim
x→1
2 − 5x + 4
x2 , if it exists.
+ 2x + 1
i. The limit does not exist.
ii. − 3
4 .
iii. 1.
iv. 0.
Math 1300 Fall 2012 Exam #3 Solutions
Solution: The answer is (iv). You can just plug in x = 1 to get 0/4. Using L’Hopital’s
rule is inappropriate here since it’s not indeterminate.
(b) Suppose a particle’s path is given parametrically by the equations x = t 2 −t and y = 3t−5.
At time t = 1, the particle is moving:
i. left and up
ii. right and up
iii. left and down
iv. right and down
Solution: The answer is (ii). Since dx/dt = 2t − 1 and dy/dt = 3, plugging in t = 1
gives dx/dt > 0 and dy/dt > 0, so that it’s moving right and up.
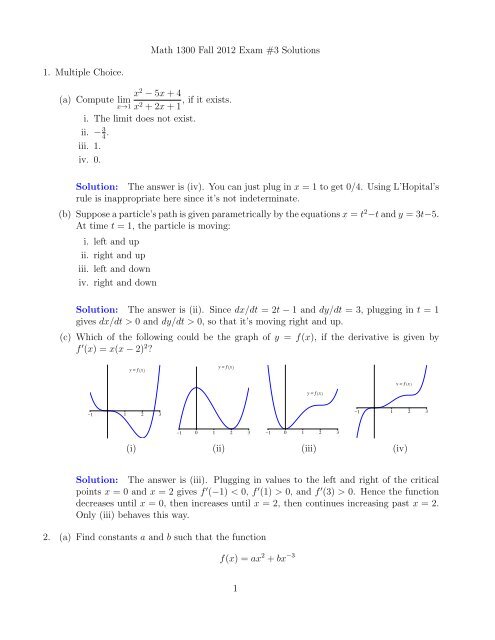
(c) Which of the following could be the graph of y = f(x), if the derivative is given by
f ′ (x) = x(x − 2) 2 ?
(i) (ii) (iii) (iv)
Solution: The answer is (iii). Plugging in values to the left and right of the critical
points x = 0 and x = 2 gives f ′ (−1) < 0, f ′ (1) > 0, and f ′ (3) > 0. Hence the function
decreases until x = 0, then increases until x = 2, then continues increasing past x = 2.
Only (iii) behaves this way.
2. (a) Find constants a and b such that the function
f(x) = ax 2 + bx −3
1

has a critical point at (1, 5).
Solution: We have f(1) = 5, so we get the equation
a + b = 5.
Also the fact that there is a critical point at x = 1 means that f ′ (1) = 0. Since
we end up with
f ′ (x) = 2ax − 3bx −4 ,
f ′ (1) = 2a − 3b = 0.
That means a = 3b,
and plugging into the first equation gives us
2
3b
+ b = 5,
2
which means 5b
= 5, or b = 2. Then solving gives a = 3.
2
So the function is
f(x) = 3x 2 + 2x −3 .
(b) For these values of a and b, is the critical point a local minimum, a local maximum, or
neither?
Solution: It’s a local minimum.
There are three ways to see this.
• Use the First Derivative Test. f ′ (x) = 6x − 6x−4 , so f ′ ( 1)
= 3 − 96 < 0 and
2
f ′ (2) = 12 − 6 > 0. 16
• Use the Second Derivative Test. f ′′ (x) = 6 + 24x−5 , so that f ′′ (1) = 30 > 0.
• Use the fact that f(x) → ∞ as x → 0 and as x → ∞. That means the function
cannot have a global maximum but must have a global minimum at the critical
point, which must therefore also be a local minimum.
3. (a) Find the tangent line to the curve 2x 2 + y 3 = 5x 3 y at the point (1, 2).
Solution: Differentiate implicitly.
2 dy
4x + 3y
dx = 15x2 3 dy
y + 5x
dx
4x − 15x 2 y = (5x 3 − 3y 2 ) dy
dx
dy
dx = 4x − 15x2y 5x3 .
− 3y2 At x = 1 and y = 2, we get
dy 4 − 30
=
dx 5 − 12
This is the slope, so the tangent line is
= 26
7 .
y = 2 + 26(x
− 1).
7
2

(b) Use the tangent line from part (a) to estimate y when x = 1.2.
Solution: When x = 1.2, we have
4. For the function
y ≈ 2 + 26
7
f(x) = x2 + 8
x + 1
· 0.2 = 96
35 .
on the interval [0, 5], find the global maximum and global minimum.
Solution: We just have to find the critical points. Compute using the Quotient Rule:
f ′ (x) = (x + 1)(2x) − (x2 + 8)(1)
(x + 1) 2
= 2x2 + 2x − x 2 − 8
(x + 1) 2
= x2 + 2x − 8
(x + 1) 2
= (x + 4)(x − 2)
(x + 1) 2 .
Critical points are where the derivative is zero or does not exist; this happens at x = −4,
x = 2, and x = −1. However only x = 2 matters because our interval is [0, 5].
We finally check f(2), f(0), and f(5). We get
f(2) = 12
3
= 4, f(0) = 8, f(5) = 33
6
= 5.5.
So the global maximum occurs at x = 0 and the global minimum occurs at x = 2.
5. (a) State precisely the Mean Value Theorem.
Solution: If f is continuous on [a, b] and differentiable everywhere on (a, b), then there
is a number c such that a < c < b and
f ′ (c) =
f(b) − f(a)
.
b − a
(b) Does the function f(x) = √ x satisfy the hypotheses of the Mean Value Theorem on the
interval [0, 4]?
Solution: Yes. It is continuous on [0, 4], and although it is not differentiable at x = 0,
it is differentiable for x > 0.
3

(c) Show that the function f(x) = √ x satisfies the conclusion of the Mean Value Theorem
on [0, 4] by finding the value c.
Solution: The slope of the secant line is
√ √
f(b) − f(a) 4 − 0
=
b − a 4 − 0
On the other hand we have f ′ (x) = 1
2 x−1/2 , so that
= 2
4
f ′ f(b) − f(a)
(c) =
b − a
1
2 c−1/2 = 1
2
c −1/2 = 1
c = 1.
= 1
2 .
6. Suppose you want to use 24 feet of fencing to enclose three separate square-shaped regions,
one which has side length x and the other two which each have side length y.
(a) Draw a picture of the situation, with labels.
Solution: I had in mind Bizarro Mickey Mouse.
(b) Find a formula for x in terms of y.
Solution: The total perimeter must be 4x + 4y + 4y = 24, which means x = 6 − 2y.
(c) What is the largest y can be? What is the smallest it can be?
Solution: The largest y could be is if x is (close to) 0, which means y = 3. The smallest
y can be is 0.
(d) Find a formula for the total area A in terms of y.
Solution:
A = x 2 + 2y 2 = 2y 2 + (6 − 2y) 2 .
4

7.
(e) What choice of y maximizes this area?
Solution: The critical point occurs when A ′ (y) = 0, so that
4y − 4(6 − 2y) = 0,
which implies that 12y = 24 or y = 2.
Plugging in the critical point and the two endpoints gives
A(0) = 36, A(2) = 8 + 4 = 12, A(3) = 18.
Hence the area is maximized when y = 0, i.e., all the fencing goes around one big square.
(f) What is x for the choice of y in part (e)?
Solution: When y = 0, we have x = 6 feet.
A lazy dog-owner has set up a laser pointer, four
feet from the nearest wall, to rotate at constant
speed of dθ/dt = 10 radians per minute, so that
the dog will chase the dot projected on the wall
around the room while the owner watches Star
Wars movies.
How fast is the dot moving along the wall when
its distance from the closest point on the wall is
x = 4 feet? (You do not need to simplify.)
Solution: The relationship between x and θ is, using the TOA part of SOH-CAH-TOA,
x
4
= tan θ,
or x = 4 tan θ. Differentiating both sides with respect to time, we get
Now at the time we care about, θ = arctan 4
4
dx
dt = 4 sec2 θ dθ
dt .
π
= arctan 1 = , and thus
4
dx
dt = 4 · sec2 (π/4) · 10 = 80 feet per minute.
5