Physical Modelling in Fluvial Geomorphology

PHYSICAL MODELLING IN FLUVIAL GEOMORPHOLOGY 231
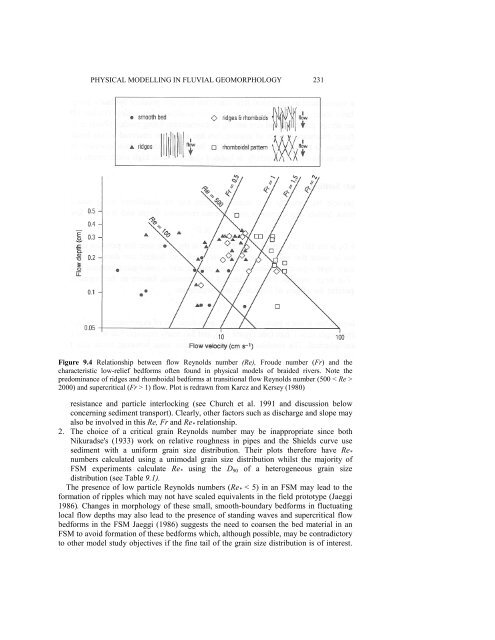
Figure 9.4 Relationship between flow Reynolds number (Re), Froude number (Fr) and the
characteristic low-relief bedforms often found in physical models of braided rivers. Note the
predominance of ridges and rhomboidal bedforms at transitional flow Reynolds number (500 < Re >
2000) and supercritical (Fr > 1) flow. Plot is redrawn from Karcz and Kersey (1980)
resistance and particle interlocking (see Church et al. 1991 and discussion below
concerning sediment transport). Clearly, other factors such as discharge and slope may
also be involved in this Re, Fr and Re* relationship.
2. The choice of a critical grain Reynolds number may be inappropriate since both
Nikuradse's (1933) work on relative roughness in pipes and the Shields curve use
sediment with a uniform grain size distribution. Their plots therefore have Re*
numbers calculated using a unimodal grain size distribution whilst the majority of
FSM experiments calculate Re* using the D90 of a heterogeneous grain size
distribution (see Table 9.1).
The presence of low particle Reynolds numbers (Re* < 5) in an FSM may lead to the
formation of ripples which may not have scaled equivalents in the field prototype (Jaeggi
1986). Changes in morphology of these small, smooth-boundary bedforms in fluctuating
local flow depths may also lead to the presence of standing waves and supercritical flow
bedforms in the FSM Jaeggi (1986) suggests the need to coarsen the bed material in an
FSM to avoid formation of these bedforms which, although possible, may be contradictory
to other model study objectives if the fine tail of the grain size distribution is of interest.