CNPA BASIC PETROLEUM GEOLOGY TRAINING - CCOP

MODULE 4
4.0 RESERVOIR ROCK EVALUATION
4.1 Porosity
4.1.1 Porosity Determination
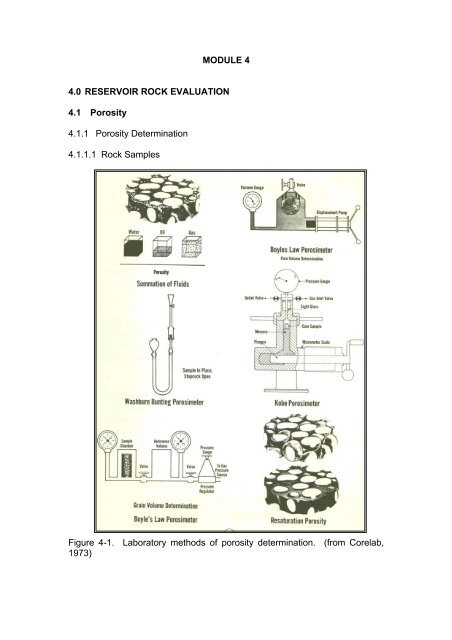
4.1.1.1 Rock Samples
Figure 4-1. Laboratory methods of porosity determination. (from Corelab,
1973)

Bulk volume is first determined by displacement of liquid, or by accurately
measuring a shaped sample and computing its volume.
Then any of the following methods are used to measure either the pore
volume or grain volume.
1. Summation of Pore Fluids – involves independent determination of
gas, oil and pore water volumes from a fresh core sample. The pore
volume is determined by adding up the three independent volumes.
2. Washburn-Bunting Method – measures pore volume by vacuum
extraction and collection of the gas (usually air) contained in the pores.
3. Liquid Resaturation – pores of a prepared sample are filled with a liquid
of known density and the weight increase of the sample is divided by
the liquid density.
4. Boyle’s Law Method – involves the compression of a gas into the pores
or the expansion of gas from the pores of a prepared sample. Either
pore volume or grain volume may be determined depending upon the
porosimeter and procedure used.
5. Grain Density – measures total porosity. After the dry weight and bulk
volume of the sample are determined, the sample is reduced to grain
size and the grain volume is determined and subtracted from the bulk
volume.
Another method of porosity determination is by petrographic analysis of thin
sections of a rock sample. This is done by point counting of pores under a
microscope. Impregnation of the sample in a vacuum with dyed resin
facilitates pore identification.
4.1.1.2 Well Logs
A common source of porosity data are the well logs. Porosity may be
calculated from the sonic, density, and neutron logs. These three logs are
usually referred to as porosity logs. Porosity may also be obtained from the
resistivity logs.

4.2 Permeability
4.2.1 Permeability Determination
4.2.1.1 Rock Samples
Figure 4-2. Laboratory measurement of permeability. (from Corelab, 1973)
Laboratory measurement of permeability usually uses air as the flow fluid and
thus the value obtained is permeability to air (K air ).
4.2.1.2 Production and Flow Test
Permeability values may also be obtained from results of flow test
4.2.1.3 Well Logs
• RFT – repeat formation test
• DST – drill stem test
New methods of quantification of permeability using well logs are also being
developed:
• Resistivity Gradient
• Porosity and Water Saturation

Absolute Permeability (k) – permeability of a rock to a fluid when the rock is
100% saturated with that fluid.
Example:
Assume a core sample, 100% saturated with brine, 2 cm 2 in cross-section and
3 cm long flows a 1 centipoise (cp) brine at the rate of 0.5 cm 3 /s under a 2
atmosphere (atm) pressure differential. Its absolute permeability is
k =
Qµ L
( P P2 ) A
1
−
=
3
(0.5 cm / s)(1
cp)(3
cm)
2
(2 atm)(2
cm )
= 0.375 darcy or 375 md
If the brine in the core sample in the above example is replaced by an oil of 3
cp viscosity under the same pressure differential and the oil flow rate is 0.167
cm 3 /s, the absolute permeability is again
k =
Qµ L
( P P ) 2
A
1
−
=
3
(0.167 cm / s)(3
cp)(3
cm)
2
(2 atm)(2
cm )
= 0.375 darcy or 375 md
Effective Permeability (k e )– permeability of a rock to a particular fluid when
that fluid has a pore saturation of less than 100%
Example:
Using the same previous example, but this time the core has 70% water
saturation (Sw=70%) and 30 % oil saturation (So=30%) and, at these and
only these saturations, under the same pressure drop it flows 0.3 cm 3 /s of the
brine and 0.02 cm 3 /s of the oil, then the effective permeability to water (k w ) is
3
Qµ
L (0.3 cm / s)(1
cp)(3
cm)
K w =
( P P ) =
= 0.225 darcy or 225 md
2
2
A (2 atm)(2
cm )
1
−
and the effective permeability to oil is
3
Qµ L (0.02 cm / s)(3
cp)(3
cm)
K o =
( P P ) =
2
2
A (2 atm)(2
cm )
1
−
= 0.045 darcy or 45 md
Relative Permeability (k r ) – the ratio of the effective permeability of a fluid at a
given value of saturation to the effective permeability of that fluid at 100%
saturation (absolute permeability), expressed as a fraction from 0 to 1.
In the example used, the relative permeabilities are
kw 0.225
ko 0.045
k rw = = = 0.60 k ro = = = 0.12
k 0. 375
k 0. 375

4.3 Relation of Permeability to Porosity
Many investigators have attempted to correlate permeability to porosity, grain
size and shape, and packing. The most frequently used relation was
developed by Kozeny as follows:
3
φ
k =
2
2
5× Sv × (1 −φ)
k = permeability, cm2 (= 1.013 x 10 8 darcies)
Φ = effective porosity
Sv = total grain surface/unit volume of reservoir, cm 2 /cm 3
The following figures show the relationship of grain size (Figure 4-1) and
sorting (Figure 4-2) to porosity and permeability.
Figure 4-1. Porosity, permeability and grain size. Porosity is not affected by
grain size but permeability increases with increase in grain size.

Figure 4-2. Porosity and permeability are affected by sorting, both increases
with better sorting.