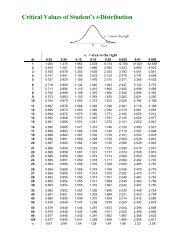
The Normal Distribution - SLC Home Page

CEGEP CHAMPLAIN - ST. LAWRENCE
201-510-LW: Business Statistics
Patrice Camiré
The Normal Distribution
1. If Z ∼ Normal(0, 1), find the following probabilities.
(a) P (Z ≤ −0.5)
(b) P (Z ≤ −1.68)
(c) P (Z ≤ 2.03)
(d) P (Z ≤ 1)
(e) P (Z ≥ −0.72)
(f) P (Z ≥ 3.05)
(g) P (−0.11 ≤ Z ≤ 1.24)
(h) P (−4 ≤ Z ≤ 0.62)
(i) P (−0.33 ≤ Z ≤ 3.6)
2. Let Z ∼ Normal(0, 1). State whether each equality is true or false. Justify.
(a) P (−z ≤ Z ≤ z) = 2P (0 ≤ Z ≤ z) , for any z > 0.
(b) P (Z ≤ −z) = P (Z ≥ z) , for any z > 0.
3. In each case, find the value of z such that the given equality is satisfied.
(a) P (Z ≤ z) = 0.67
(b) P (Z ≥ z) = 0.9821
(c) P (−z ≤ Z ≤ z) = 0.9
(d) P (−z ≤ Z ≤ z) = 0.04
4. In order to be accepted to a given private high school, a student must write an entry exam. Data has
shown that the results are normally distributed with a mean of 72 and a standard deviation of 9. If
only the top 10% of the students are accepted, what is the minimum score needed on the entry exam
for a student to be accepted?
5. (a) If X ∼ Normal(8, 3), then find P (X ≤ 7).
(b) If X ∼ Normal(70, 12), then find P (X ≥ 80).
(c) If X ∼ Normal(1, 4), then find P (0 ≤ X ≤ 2).
(d) If X ∼ Normal(−3, 2.1), then find P (−3 ≤ X ≤ 0).
6. In a large company, the age of an employee working in accounting is normally distributed with a mean
of 45 years and a standard deviation of 10 years.
(a) If an employee working in accounting is randomly selected, what is the probability that he/she is
between 30 and 35 years old?
(b) The oldest 20% of employees working in accounting are older than what age?
(c) If 20 employees working in accounting are randomly selected, what is the probability that their
mean age is less than 40?
7. The score of a student on a test was found to be normally distributed with a mean of 75 and a standard
deviation of 8. What is the probability that the average grade in a class of 30 students exceeds 70?
8. According to Statistics Canada, the average weekly earnings of Quebecers was $784 in 2010. (Assume
a normal distribution with a standard deviation of $100.) If you randomly select 50 workers in the
province, what is the probability that their average weekly earnings are between $800 and $900?

9. In a large company, an employee works on average 40 hours a week with a standard deviation of 6
hours. If 15 employees are selected at random, what is the probability that their mean weekly working
hours is less than 38 hours? (Assume normality.)
Answers
1. (a) 0.3085
(b) 0.0465
(c) 0.9788
(d) 0.8413
(e) 0.7642
(f) 0.0011
(g) 0.4363
(h) 0.7324
(i) 0.6293
2. Both equalities are true since the standard normal distribution is symmetric about 0.
3. (a) z = 0.44
(b) z = −2.1
(c) z = 1.64 or z = 1.65
(d) z = 0.05
4. 84
5. (a) 0.3707 (b) 0.2033 (c) 0.1974 (d) 0.4236
6. (a) 0.0919
(b) ≈ 53.4 years old
(c) 0.0125
7. 0.9997
8. 0.1292
9. 0.0985