Vickrey's Second Price Auction

Vickrey’s Second Price Auction
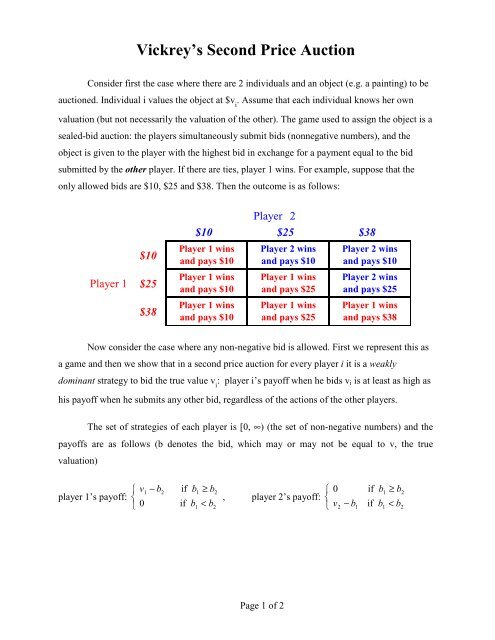
Consider first the case where there are 2 individuals and an object (e.g. a painting) to be
auctioned. Individual i values the object at $v i
. Assume that each individual knows her own
valuation (but not necessarily the valuation of the other). The game used to assign the object is a
sealed-bid auction: the players simultaneously submit bids (nonnegative numbers), and the
object is given to the player with the highest bid in exchange for a payment equal to the bid
submitted by the other player. If there are ties, player 1 wins. For example, suppose that the
only allowed bids are $10, $25 and $38. Then the outcome is as follows:
$10
Player 1 $25
$38
Player 2
$10 $25 $38
Player 1 wins
and pays $10
Player 1 wins
and pays $10
Player 1 wins
and pays $10
Player 2 wins
and pays $10
Player 1 wins
and pays $25
Player 1 wins
and pays $25
Player 2 wins
and pays $10
Player 2 wins
and pays $25
Player 1 wins
and pays $38
Now consider the case where any non-negative bid is allowed. First we represent this as
a game and then we show that in a second price auction for every player i it is a weakly
dominant strategy to bid the true value v i
: player i’s payoff when he bids v i is at least as high as
his payoff when he submits any other bid, regardless of the actions of the other players.
The set of strategies of each player is [0, ∞) (the set of non-negative numbers) and the
payoffs are as follows (b denotes the bid, which may or may not be equal to v, the true
valuation)
player 1’s payoff:
⎧
⎨
⎩
v − b if b ≥ b
0
1 2 1 2
if
b
< b
1 2
, player 2’s payoff:
⎧
⎨
⎩
if
b
≥ b
0
1 2
v − b if b < b
2 1 1 2
Page 1 of 2

THEOREM: For every player i = 1,2 it is a dominant strategy to bid b i
= v i
.
Proof. We shall prove that choosing b 1
= v 1
is a dominant strategy for player 1 (the proof
for player 2 is similar). Player 1 does not know what bid player 2 is going to submit. We want
to show that, whatever bid player 2 submits, player 1 cannot get a higher payoff by submitting a
bid different from v 1
. We need to distinguish three cases. CASE 1: b 2
< v 1
, CASE 2: b 2
> v 1
,
CASE 3: b 2
= v 1
.
Consider Case 1 first (b 2
< v 1
). Bidding v 1
gives player 1 a payoff of v 1
− b 2
> 0.
Consider a different bid x 1
. If x 1
≥ b 2
then player 1 still gets the good and a payoff of v 1
− b 2
.
Thus such a bid is not better than v 1
. If x 1
< b 2
then the good goes to player 2 and player 1 gets
a payoff of 0. Thus in this case she is worse off.
Consider now Case 2 (b 2
> v 1
). Bidding v 1
gives a payoff of 0. So does bidding any x 1
<
b 2
. If, on the other hand, she were to bid x 1
≥ b 2
then she would get a payoff of v 1
− b 2
< 0.
Finally, consider Case 3 (b 2
= v 1
). In this case, whatever player 1 bids her payoff is zero
(either she does not get the object or she does, in which case her payoff is v 1
−b 2
= 0).
The above theorem is true also if there are more than two players: for each player it is a
dominant strategy to bid his/her own true value.
Note: e-bay auctions are second-price auctions.
The second highest bid is the highest bid among the ones that remain after removing
the bid of the winner. For example, if there are three players and the bids are ($50, $50, $40)
and player 1 is the winner, then after you remove the bid of player 1 your are left with the bids
of players 2 and 3, namely $50 and $40 and the higher of these is $50, so that player 1 (the
winner) ends up paying $50. Hence, if there are no ties, then the winner ends up paying less
than her bid, but if there are ties at the top (that is, the highest bid is submitted by more than
one player) then the winner ends up paying an amount equal to her own bid.
Page 2 of 2