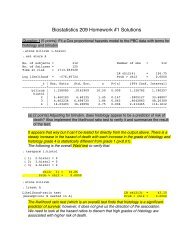
Sample Size Calculations for Analytic Studies

Sample Size Calculations for Analytic Studies 

• Solving standard problems in Stata 

• Stata solutions to some non-standard problems: 

– Adjusting for covariates 

– Mediation 

– Clustered data 

– Pre-post trial designs 

– Fixed sample size 

– Categorical predictors and outcomes 

1

Standard problems 

• Method for calculating sample size depends on 

– Predictor type: continuous, binary 

– Outcome type: continuous, binary, failure time 

– Effect size 

– α, 1- or 2-sided test, power 

2

Binary predictor, continuous outcomes 

• Predictor prevalence 0.5 (e.g., RCTs with 1-1 allocation): 

– use Table 6.A. for comparing means in Designing 

Clinical Research (DCR) 

• Arbitrary predictor prevalence: 

– use sampsi function in Stata 

3

Basic set-up using sampsi 

Equal allocation to groups, means of 1.4 and 1.9, SD of 

outcome = 2 in both groups 

. sampsi 1.4 1.9, sd1(2) 

Estimated sample size for two-sample comparison of means 

Test Ho: m1 = m2, where m1 is the mean in population 1 

and m2 is the mean in population 2 

Assumptions: 

alpha = 0.0500 (two-sided) 

power = 0.9000 

m1 = 1.4 

m2 = 1.9 

sd1 = 2 

sd2 = 2 

n2/n1 = 1.00 

Estimated required sample sizes: 

n1 = 337 

n2 = 337 

4

A more complicated example 

60% in group 2, means 1.4 and 1.6, SDs of 0.85 and 1.05, 

one-sided test 

. local r = .6/.4 

. sampsi 1.4 1.6, sd1(0.85) sd2(1.05) r(‘r’) power(0.8) onesided 




Assumptions: 

alpha = 0.0500 (one-sided) 

power = 0.8000 

m1 = 1.4 

m2 = 1.6 

sd1 = .85 

sd2 = 1.05 

n2/n1 = 1.50 


n1 = 226 

n2 = 339 

Note: Use sampncti for large effect sizes; requires nct2 package 

5

Continuous predictor, continuous outcome 

• If you can pose problem in terms of correlation coefficient: 

– use Table 6.C for in DCR 

– use sampsi rho in STATA 

• If you can pose problem in terms of slope, SDs of 

predictor and outcome: 

– use sampsi reg 

6

Continuous predictor, continuous outcome, 

using sampsi rho 

Correlation of predictor and outcome = 0.3 

. sampsi_rho, alt(0.3) power(0.8) 

Estimated sample size for Pearson Correlation 

Test Ho: Rho alt = Rho null, usually null Rho is 0 

Assumptions: 

Alpha = 0.0500 (two-sided) 

Power = 0.8000 

Null Rho = 0.0000 

Alt Rho = 0.3000 

Estimated required sample size: 

n = 84.927811 

7

Continuous predictor, continuous outcome, 

using sampsi reg 

Regression coefficient = 0.3, SD of predictor and outcome = 1 

. sampsi_reg, alt(0.3) sx(1) sy(1) varmethod(sdy) power(0.8) 

Estimated sample size for linear regression 

Test Ho: slope alt = slope null, usually null slope is 0 

Assumptions: 

Alpha = 0.0500 (two-sided) 

Power = 0.8000 

Null Slope = 0.0000 

Alt Slope = 0.3000 

Residual sd = 0.9539 

SD of X’s = 1.0000 

SD of Y’s = 1.0000 

Estimated required sample size: 

n = 82 

8

Binary predictor, binary outcome 

• Predictor prevalence 0.5 

– use Table 6.B. for comparing proportions in DCR 

• Arbitrary predictor prevalence: 

– use sampsi function in Stata 

9

Binary predictor, binary outcome 

Exposure prevalence 2/3, outcome prevalence 20% in 

unexposed, 30% in exposed 

. sampsi 0.2 0.3, r(2) power(0.8) 

Estimated sample size for two-sample comparison of proportions 

Test Ho: p1 = p2, where p1 is the proportion in population 1 

and p2 is the proportion in population 2 

Assumptions: 


power = 0.8000 

p1 = 0.2000 

p2 = 0.3000 

n2/n1 = 2.00 


n1 = 239 

n2 = 478 

10

Continuous predictor, binary outcome 

• Use methods for binary predictor, continuous outcome 

– set r = p/(1 − p) where p is prevalence of outcome 

– if you know means and SDs of continuous predictor in 

cases and controls, use sampsi as usual 

– otherwise, set up using log-OR and SD of predictor 

11


Case-control study with 3 controls per case, mean of 

predictor 0.2 in controls, 0.4 in cases, SD of predictor 0.5 in 

both groups 

. sampsi 0.2 0.4, r(.33) sd1(0.5) 




Assumptions: 


power = 0.9000 

m1 = .2 

m2 = .4 

sd1 = .5 

sd2 = .5 

n2/n1 = 0.33 


n1 = 265 

n2 = 88 

12


Cross-sectional study with outcome prevalence = 33%, OR 

per unit increase in predictor = 1.5, SD of predictor = 0.5: 

effect size equal to log(OR) × SD of predictor 

. local delta = log(1.5)*0.5 

. sampsi 0 ‘delta’, r(0.5) sd1(1) power(0.8) 




Assumptions: 


power = 0.8000 

m1 = 0 

m2 = .202733 

sd1 = 1 

sd2 = 1 

n2/n1 = 0.50 


n1 = 573 

n2 = 287 

13

Failure time outcomes 

• Use stpower in STATA 

– stpower cox for Cox models 

– stpower logrank for unadjusted log-rank test 

– stpower exponential for trials with long accrual 

14

Continuous predictor, failure time outcome 

Overall cumulative incidence of 15%, 10% early dropout, SD 

of predictor 1.5, hazard-ratio per unit increase in predictor 1.2 

. stpower cox, failprob(0.15) wdprob(0.10) sd(1.5) hratio(1.2) 

Estimated sample size for Cox PH regression 

Wald test, log-hazard metric 

Ho: [b1, b2, ..., bp] = [0, b2, ..., bp] 

Input parameters: 

alpha = 0.0500 (two sided) 

b1 = 0.1823 

sd = 1.5000 

power = 0.8000 

Pr(event) = 0.1500 

withdrawal(%) = 10.00 

Estimated number of events and sample size: 

E = 105 

N = 778 

15

Binary predictor, failure time outcome 

RCT, overall cumulative incidence of 15%, 10% early 

dropout, hazard-ratio for treatment = 0.75, 1-1 allocation so 

SD of predictor = √ 0.5(1 − 0.5) = 0.5 (the default) 

. stpower cox, failprob(0.15) wdprob(0.10) hratio(0.75) 



Ho: [b1, b2, ..., bp] = [0, b2, ..., bp] 



b1 = -0.2877 

sd = 0.5000 

power = 0.8000 

Pr(event) = 0.1500 



E = 380 

N = 2811 

16


Overall cumulative incidence of 15%, 10% early dropout, 

prevalence of exposure 25%, hazard-ratio for exposure 1.5 

. local sd = sqrt(0.25*(1-0.25)) 

. stpower cox, failprob(0.15) wdprob(0.10) hratio(1.50) sd(‘sd’) 



Ho: [b1, b2, ..., bp] = [0, b2, ..., bp] 



b1 = 0.4055 

sd = 0.4330 

power = 0.8000 

Pr(event) = 0.1500 



E = 255 

N = 1887 

17

Adjustment for covariates 

• Suppose that 

– multiple correlation of primary predictor with 

covariates is ρ 

– equivalently R 2 for linear regression of primary 

predictor on covariates is ρ 2 

• Implemented in stpower using r2() option 

• Alternatively, compute sample size using sampsi, inflate 

result by 1/(1 − ρ 2 ) 

• Hsieh recommends ρ = 0.3 → 10% inflation of N 

• NB: Adjusted effect size usually smaller than unadjusted 

18


Same problem as before; correlation of exposure with 

covariates ρ = 0.5, so R 2 = 0.5 2 = 0.25 

. local sd = sqrt(0.25*(1-0.25)) 

. stpower cox, failprob(0.15) wdprob(0.10) hratio(1.50) sd(‘sd’) r2(0.25) 



Ho: [b1, b2, ..., bp] = [0, b2, ..., bp] 



b1 = 0.4055 

sd = 0.4330 

power = 0.8000 

Pr(event) = 0.1500 

R2 = 0.2500 



E = 340 

N = 2515 

19

Adjustment for covariates: 

binary predictor, continuous outcome 

Prevalence of exposure 40%, Effect size 0.25, ρ = 0.3 

. local r = 0.4/0.6 

. sampsi 0 0.25, sd1(1) r(‘r’) power(0.8) 




Assumptions: 


power = 0.8000 

m1 = 0 

m2 = .25 

sd1 = 1 

sd2 = 1 

n2/n1 = 0.67 


n1 = 314 

n2 = 210 

. dis round((314+210)/(1-0.3^2)) 

576 

20

Sample size to show mediation 

• To show mediation, we need to show that 

1. primary predictor associated with mediator 

2. mediator independently associated with outcome, 

adjusting for primary predictor 

3. coefficient for primary predictor changes when 

mediator added to the regression model 

• If 1 holds, then 2 implies 3 

• Determine sample size needed to show 2: 

– mediator independently predicts outcome, adjusting 

for primary predictor and covariates 

21

Mediation example 

Cox model, cumulative incidence 25%, early dropout 15%, 

adjusted HR per SD increase in continuous mediator 1.2, 

correlation of mediator w/ primary predictor, covariates 0.2 

. stpower cox, failprob(0.25) wdprob(0.15) hratio(1.2) sd(1) r2(0.04) 



Ho: [b1, b2, ..., bp] = [0, b2, ..., bp] 



b1 = 0.1823 

sd = 1.0000 

power = 0.8000 

Pr(event) = 0.2500 

R2 = 0.0400 



E = 246 

N = 1158 

22

Cluster randomized trials 

• Clusters of average size n c are randomized 1-1 to 

treatment or control 

• Compute number of patients for trial ignoring clustering 

• Inflate N by “design effect”: 1 + ρ(n c − 1), where ρ is the 

within-cluster correlation 

• sampclus implements this after sampsi (but not 

stpower) 

23


Binary outcome, incidence 30% in control, 20% in treatment, 

1-1 allocation of clusters, n c = 25, ρ = 0.02 

. sampsi 0.3 0.2 

Estimated sample size for two-sample comparison of proportions 

Test Ho: p1 = p2, where p1 is the proportion in population 1 

and p2 is the proportion in population 2 

Assumptions: 


power = 0.9000 

p1 = 0.3000 

p2 = 0.2000 

n2/n1 = 1.00 


n1 = 412 

n2 = 412 

. dis round(412*(1+0.02*24)) 

610 

24

. sampclus, obsclus(25) rho(0.02) 


Sample Size Adjusted for Cluster Design 

n1 (uncorrected) = 412 

n2 (uncorrected) = 412 

Intraclass correlation = .02 

Average obs. per cluster = 25 

Minimum number of clusters = 49 

Estimated sample size per group: 

n1 (corrected) = 610 

n2 (corrected) = 610 

25

Randomized trials, within-cluster randomization 

• Patients are randomized 1-1 to treatment or control 

within clusters 

• Design effect is 1 − ρ, does not depend on n c 

• Compute sample size ignoring clustering, multiply result 

by 1 − ρ 

26

Clustered data: complex surveys 

• Design effects vary by predictor and outcome, can be less 

than 1 

• Simple rules do not apply 

• Use design effect to adjust sample size calculated 

assuming independence, if you can get a reasonable 

estimate 

27

RCTs measuring change in a continuous outcome 

• Outcome measured at baseline and follow-up 

• No expected difference in means at baseline (why?) 

• Analysis options 

– analyze follow-up outcome, ignoring baseline 

– analyze change scores 

– analyze follow-up outcome, adjusting for baseline 

(ANCOVA) 

• Use sampsi 

28

RCT measuring change in continuous outcome 

1-1 allocation, equal baseline means, effect size at follow-up 

0.5 SD, correlation of baseline and follow-up outcome 0.3 

. sampsi 0 0.5, sd1(1) pre(1) post(1) r01(.3) 

Estimated sample size for two samples with repeated measures 

Assumptions: 


power = 0.9000 

m1 = 0 

m2 = .5 

sd1 = 1 

sd2 = 1 

n2/n1 = 1.00 

number of follow-up measurements = 1 

number of baseline measurements = 1 

correlation between baseline & follow-up = 0.300 

29

RCT measuring change in continuous outcome 

Method: POST 

relative efficiency = 1.000 

adjustment to sd = 1.000 

adjusted sd1 = 1.000 


n1 = 85 

n2 = 85 

Method: CHANGE 





n1 = 118 

n2 = 118 

Method: ANCOVA 





n1 = 77 

n2 = 77 

30

Same design, but with pre-post correlation of 0.7 

Method: POST 





n1 = 85 

n2 = 85 

Method: CHANGE 





n1 = 51 

n2 = 51 

Method: ANCOVA 





n1 = 43 

n2 = 43 

31

If sample size is fixed 

• In secondary analyses, sample size usually a done deal 

• sampsi can compute power for fixed N and effect size 

• stpower can compute either power or minimum 

detectable effects when other inputs are specified 

• In grants, power for a well-motivated effect size more 

convincing than minimum detectable effects 

32

Power for fixed sample and effect sizes 

Cox model, N=2515, 15% overall cumulative incidence, 10% 

dropout, 25% exposed, HR for exposure 1.5 

. local sd = sqrt(0.25*(1-0.25)) 

. local n = round(2515*0.9) 

. stpower cox, failprob(0.15) hratio(1.3(0.1)1.6) sd(‘sd’) r2(0.25) n(‘n’) 

Estimated power for Cox PH regression 


Ho: [b1, b2, ..., bp] = [0, b2, ..., bp] 

+------------------------------------------------------------------------+ 

| Power N E B1 SD Alpha* Pr(E) R2 | 

|------------------------------------------------------------------------| 

| .441616 2264 340 .262364 .433013 .05 .15 .25 | 

| .64254 2264 340 .336472 .433013 .05 .15 .25 | 

| .800117 2264 340 .405465 .433013 .05 .15 .25 | 

| .901134 2264 340 .470004 .433013 .05 .15 .25 | 

+------------------------------------------------------------------------+ 

33

Minimum detectable hazard ratios 

Same set-up as last slide 

. local sd = sqrt(0.25*(1-0.25)) 

. local n = round(2515*0.9) 

. stpower cox, failprob(0.15) sd(‘sd’) r2(0.25) n(‘n’) power(0.9) hr 

Estimated hazard ratio for Cox PH regression 

Wald test, hazard metric 

Ho: [b1, b2, ..., bp] = [0, b2, ..., bp] 



sd = 0.4330 

N = 2264 

power = 0.9000 

Pr(event) = 0.1500 

R2 = 0.2500 

Estimated number of events and hazard ratio: 

E = 340 

hratio = 0.6256 

. dis 1/.6256 

1.5984655 

34

Categorical predictors and outcomes 

• Categorical predictors: 

– compute Ns for pairwise differences with reference 

group (multiple comparisons) 

– for overall effect, use fpower or simpower functions in 

STATA 

http://www.ats.ucla.edu/stat/stata/dae/fpower.htm 

• Categorical outcomes 

– nominal outcomes: compute Ns for pairwise 

differences with reference group 

– ordinal outcomes: Whitehead paper gives methods 

available for proportional odds model, but n/a in 

Stata 

35

Summary 

• Stata sampsi and stpower commands can do a lot, 

including making tables 

• stpower can account for covariate adjustment; with 

sampsi inflate sample size by 1/(1 − ρ 2 ) 

• Handle mediation like a confounding problem 

• sampclus can inflate sample size for cluster-randomized 

trials with continuous or binary endpoint; for Cox model, 

inflate sample size by design effect 1 + ρ(n c − 1) 

• sampsi can handle simple pre-post designs 

• Downloadable Stata packages (and your biostat mentors) 

can deal with more complicated problems 

36

Sample Size Calculations for Analytic Studies

Create successful ePaper yourself

Delete template?

Save as template?