Polynomial Functions & Properties of Polynomials General ...

Polynomial Functions & Properties of Polynomials
General Polynomial Concepts
A polynomial function has the form f x=a n
x n a n−1
x n−1 a n−2
x n−2 a 2
x 2 a 1
xa 0
,
where a n
,a n−1
,a n−2
,,a 2,
a 1,
a 0 are real numbers and n is a non-negative integer. In other
words, a polynomial is the sum of one or more monomials with real coefficients and nonnegative
integer exponents.
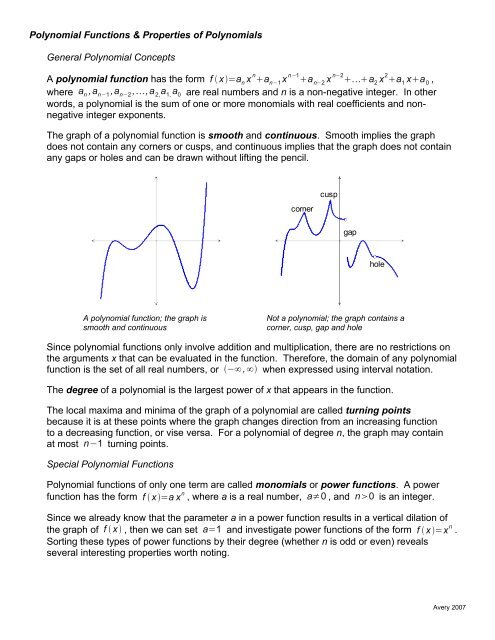
The graph of a polynomial function is smooth and continuous. Smooth implies the graph
does not contain any corners or cusps, and continuous implies that the graph does not contain
any gaps or holes and can be drawn without lifting the pencil.
corner
cusp
gap
hole
A polynomial function; the graph is
smooth and continuous
Not a polynomial; the graph contains a
corner, cusp, gap and hole
Since polynomial functions only involve addition and multiplication, there are no restrictions on
the arguments x that can be evaluated in the function. Therefore, the domain of any polynomial
function is the set of all real numbers, or −∞,∞ when expressed using interval notation.
The degree of a polynomial is the largest power of x that appears in the function.
The local maxima and minima of the graph of a polynomial are called turning points
because it is at these points where the graph changes direction from an increasing function
to a decreasing function, or vise versa. For a polynomial of degree n, the graph may contain
at most n−1 turning points.
Special Polynomial Functions
Polynomial functions of only one term are called monomials or power functions. A power
function has the form f x=a x n , where a is a real number, a≠0 , and n0 is an integer.
Since we already know that the parameter a in a power function results in a vertical dilation of
the graph of f x , then we can set a=1 and investigate power functions of the form f x=x n .
Sorting these types of power functions by their degree (whether n is odd or even) reveals
several interesting properties worth noting.
Avery 2007

Properties of Power Functions f x=x n , for n an Odd Integer:
1. The graph is symmetric with respect to the
origin, so f is odd.
2. The domain and the range are the set of all
real numbers. Using interval notation, the
domain is −∞,∞ and the range is −∞,∞ .
3. The graph always contains the points 0 ,0 ,
1,1 , and −1,−1 .
4. As n increases in magnitude, the graph
becomes more vertical for ∣x∣1 , but becomes
flatter (and closer to the x-axis) for ∣x∣1 .
Properties of Power Functions f x=x n , for n an Even Integer:
1. The graph is symmetric with respect to the
y-axis, so f is even.
2. The domain is the set of all real numbers,
and the range is the set of non-negative real
numbers. Using interval notation, the domain
is −∞ ,∞ and the range is [ 0,∞ ) .
3. The graph always contains the points 0 ,0 ,
1,1 , and −1,1 .
4. As n increases in magnitude, the graph
becomes more vertical for ∣x∣1 , but becomes
flatter (and closer to the x-axis) for ∣x∣1 .
End Behavior of a Polynomial Function
End behavior is the term used to describe how the graph of a function behaves for large values
of ∣x∣. For the polynomial f x=a n
x n a n−1
x n−1 a n−2
x n−2 a 2
x 2 a 1
xa 0
, the graph will
exhibit end behavior that resembles the graph of f x=a n
x n . This is because the leading term
of the polynomial “dominates” the polynomial for large values of ∣x∣. Using what we know about
power functions, there are only four types of end behavior for a polynomial function.
n≥2even;a n
0 n≥2even;a n
0 n≥3odd; a n
0 n≥3odd; a n
0
Avery 2007

Zeros of a Polynomial Function
From past experience with quadratic functions (which are polynomial functions) we know that
zeros can be real, imaginary, or complex (the zero has a real part and an imaginary part). We
will focus on real zeros at this time and discuss complex zeros in greater detail in the near future.
For a polynomial function f, any number r for which f r =0 is called a zero or root of the
function f. Moreover, if r is a zero of f, then x −r is a factor of f. Finally, if r is a real zero of f,
then r is an x-intercept of the graph of f.
When a polynomial function is completely factored, each of the factors help identify zeros of the
function. However, since the same factor can occur multiple times, it follows that a zero can
occur multiple times. If x−r is a factor of a polynomial m times but not m1 times, then r is
a zero of the polynomial m times, and we say that r is a zero of multiplicity m.
If r is a zero of a polynomial f an even number of times, then r is said to be a zero of even
multiplicity. Three ways to see that r is a zero of even multiplicity are:
When completely factored, x−r is a factor of f an even number of times, so the power of
x−r is even.
The sign of f x does not change from one side of r to the other side of r. In other words,
if the value of the polynomial f at an argument near r is positive, then the value of the
polynomial f at an argument near r, but on the other side of r, will also be positive. If the
value of the polynomial f at an argument near r is negative, then the value of the polynomial
f at an argument near r, but on the other side of r, will also be negative.
The graph of the polynomial f x touches the x-axis at r.
If r is a zero of a polynomial f an odd number of times, then r is said to be a zero of odd
multiplicity. Three ways to see that r is a zero of odd multiplicity are:
When completely factored, x−r is a factor of f an odd number of times, so the power of
x−r is odd.
The sign of f x changes from one side of r to the other side of r. In other words, if the
value of the polynomial f at an argument near r is positive, then the value of the polynomial
f at an argument near r, but on the other side of r, will be negative. If the value of the
polynomial f at an argument near r is negative, then the value of the polynomial f at an
argument near r, but on the other side of r, will be positive.
The graph of the polynomial f x crosses the x-axis at r.
Avery 2007