Creating linear models for data

Student: Class: Date:
Creating linear models for data
Student Activity Sheet 4; use with Exploring “Transformations on linear functions”
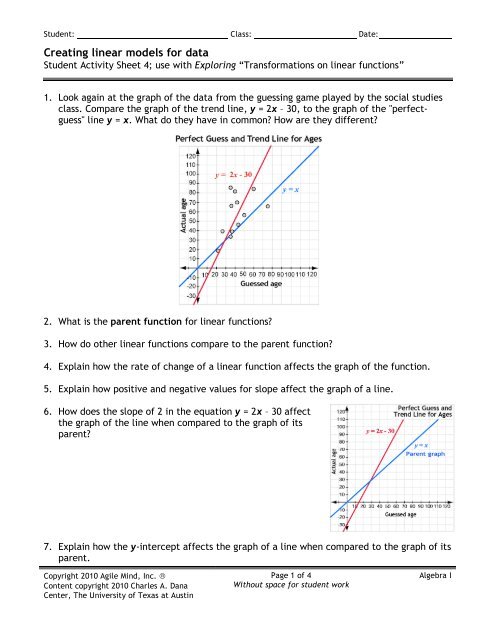
1. Look again at the graph of the data from the guessing game played by the social studies
class. Compare the graph of the trend line, y = 2x – 30, to the graph of the "perfectguess"
line y = x. What do they have in common? How are they different?
2. What is the parent function for linear functions?
3. How do other linear functions compare to the parent function?
4. Explain how the rate of change of a linear function affects the graph of the function.
5. Explain how positive and negative values for slope affect the graph of a line.
6. How does the slope of 2 in the equation y = 2x – 30 affect
the graph of the line when compared to the graph of its
parent?
7. Explain how the y-intercept affects the graph of a line when compared to the graph of its
parent.
Copyright 2010 Agile Mind, Inc. ®
Content copyright 2010 Charles A. Dana
Center, The University of Texas at Austin
Page 1 of 4
Without space for student work
Algebra I

Student: Class: Date:
Creating linear models for data
Student Activity Sheet 4; use with Exploring “Transformations on linear functions”
8. In the equation y = 2x – 30, how does the y-intercept of -30
affect the line compared to its parent?
9. How would you transform the graph of y = x to produce
the graph of y = 3x + 1?
10. How would you transform the graph of y = x to produce
1
the graph of y = x -3?
2
Copyright 2010 Agile Mind, Inc. ®
Content copyright 2010 Charles A. Dana
Center, The University of Texas at Austin
Page 2 of 4
Without space for student work
Algebra I

Student: Class: Date:
Creating linear models for data
Student Activity Sheet 4; use with Exploring “Transformations on linear functions”
11. How would you transform the graph of y = x to produce the
graph of y = -3x + 2?
12. Explain in terms of transformations how the graphs of y = 16 + 0.07x and
y = 26.1 + 0.07x are related to each other.
13. What characteristics of the graph of the parent function, y = x, do you have to change to
get each of these graphs?
Complete the following puzzle (questions 14–18) by matching the graph of each
transformation with its verbal description. Write the letter of the graph in the space
beside its verbal description. Some graphs may be used more than once.
14. The graph of y = 3x – 2 shifted up 4 units.
15. The graph y = x with a rate of change of 2 and shifted down 1 unit.
3
16. The linear parent function reflected across the x-axis and shifted up 2.
17. The graph y = x shifted up 2 and with a rate of change of 3.
2
18. The graph of y = - x -5 reflected over the x-axis and shifted down 6 units.
3
Copyright 2010 Agile Mind, Inc. ®
Content copyright 2010 Charles A. Dana
Center, The University of Texas at Austin
Page 3 of 4
Without space for student work
Algebra I

Student: Class: Date:
Creating linear models for data
Student Activity Sheet 4; use with Exploring “Transformations on linear functions”
19. REEI INFFORRCCEE For each transformation described below, sketch the graph that results.
Then, write the function rule that represents the transformation. Use a single graph grid
for all four graphs, and label each graph with the appropriate letter.
a. Shift the graph of y = x down 2 units.
Function rule:
b. Shift the graph from part a up 5 units.
Function rule:
c. Reflect the graph from part b over the x-axis.
Function rule:
d. Create a graph with the same y-intercept as the graph in part c, but with 4 times the
rate of change.
Function rule:
Copyright 2010 Agile Mind, Inc. ®
Content copyright 2010 Charles A. Dana
Center, The University of Texas at Austin
Page 4 of 4
Without space for student work
Algebra I