Examples of Use of Significant Figures/Error Propagation in Problems

Significant Figures in Calculations
Error Analysis
Every lab report must have an error analysis. For many experiments, significant figure
rules are sufficient. Remember to carry at least one extra significant figure to avoid round
off error through intermediate calculations. Non-significant figures are often written
smaller or like "subscripts" to avoid confusion. For example, 0.1234 ± 0.0001 would be
written 0.123 4 . On the other hand, 0.1234 ± 0.003 would be written 0.12 3 or 0.12 34 .
Keeping track of significant figures in long calculations is easy. Just underline the
insignificant digit for all the intermediate and final results using a pen or pencil. To find
the uncertainties and approximate number of significant figures when using volumetric
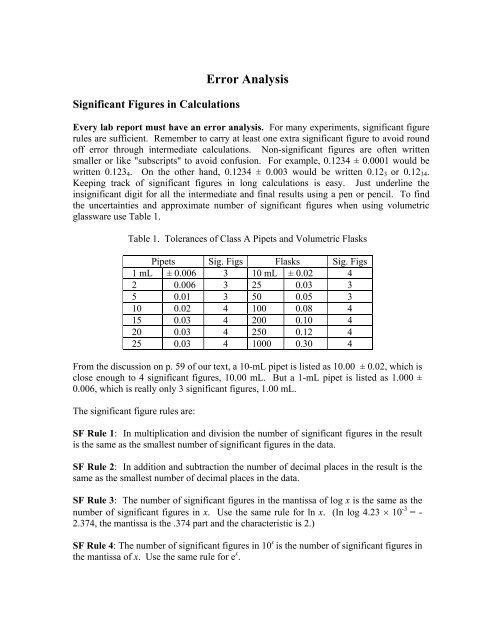
glassware use Table 1.
Table 1. Tolerances of Class A Pipets and Volumetric Flasks
Pipets Sig. Figs Flasks Sig. Figs
1 mL ± 0.006 3 10 mL ± 0.02 4
2 0.006 3 25 0.03 3
5 0.01 3 50 0.05 3
10 0.02 4 100 0.08 4
15 0.03 4 200 0.10 4
20 0.03 4 250 0.12 4
25 0.03 4 1000 0.30 4
From the discussion on p. 59 of our text, a 10-mL pipet is listed as 10.00 ± 0.02, which is
close enough to 4 significant figures, 10.00 mL. But a 1-mL pipet is listed as 1.000 ±
0.006, which is really only 3 significant figures, 1.00 mL.
The significant figure rules are:
SF Rule 1: In multiplication and division the number of significant figures in the result
is the same as the smallest number of significant figures in the data.
SF Rule 2: In addition and subtraction the number of decimal places in the result is the
same as the smallest number of decimal places in the data.
SF Rule 3: The number of significant figures in the mantissa of log x is the same as the
number of significant figures in x. Use the same rule for ln x. (In log 4.23 × 10 -3 = -
2.374, the mantissa is the .374 part and the characteristic is 2.)
SF Rule 4: The number of significant figures in 10 x is the number of significant figures in
the mantissa of x. Use the same rule for e x .

Example 1: Concentration Calculations: A solution is made by transferring 1 mL of a
0.1245 3 M solution, using a volumetric pipet, into a 200-mL volumetric flask. Calculate
the final concentration.
Solution: The 1-mL volumetric pipet has 3 significant figures; all the other values have
4. The calculations all involve multiplication and division, so the final answer should be
expressed with 3 significant figures.
1.00 × 0.1245 3 M / 200.0 = 0.000622 6 M = 6.22 × 10 -4 M
Example 2: Logs: The equilibrium constant for a reaction at two different temperatures
is 0.032 2 at 298.2 and 0.47 3 at 353.2 K. Calculate ln(k 2 /k 1 ).
Solution: Both k’s have 2 significant figures, so k 2 /k 1 should also have 2 significant
figures: k 2 /k 1 = 13. 89 . Then using SF Rule 3 shows that ln k 2 /k 1 should have 2 significant
figures in the “mantissa:”
ln k 2 /k 1 = ln 13. 89 = 2.63 1
Example 3: Antilogs: The rate of a reaction depends on temperature as ln k = ln A –
E a/ RT. Using curve fitting it was found that ln A = 9.87 4 . Calculate A.
87
Solution: The result is e 9.
4
= 1.9427 × 10
4 . The mantissa has only 2 significant figures,
so the result should only have two significant figures (SF Rule 4).
1.9 4 × 10 4 , or just 1.9 × 10 4
Example 4: Antilogs: The rate of a reaction depends on temperature as ln k = ln A –
E a /RT. Using curve fitting it was found that ln A = 9.87 4 and E a = 28.2 6 kJ/mol. Calculate
k at T = 298.15 K.
Solution: The result for ln k has 2 significant figures: both ln A and E a have 3 significant
figures (SF Rule 1), but the difference has only one past the decimal point:
ln k = 9.87 4 – 28.2 6 × 10 3 /[(8.314)(298.15)] = 9.87 4 – 11.4 0 = -1.5 266
The mantissa has only 1 significant figure. Then solving for k and using SF Rule 4 gives
k = −1
5 266
= 0.217 or finally just 0.2
e .

Propagation of Errors
Significant figure rules are sufficient when you do not have good estimates for the
measurement errors. If you do have good estimates for the measurement errors then a
more careful error analysis based on propagation of error rules is appropriate. Least
squares curve fitting provides very good estimates for uncertainties. For error analysis
with the slope or intercept from least squares curve fitting, a little more care is justified
than is provided by significant figure rules. Use propagation of error rules to find the
error in final results derived from curve fitting.
The propagation of error rules are listed below. The variance of x, (σ x ) 2 , is the square of
the standard deviation, σ x (an e can also denote the error or uncertainty and an s the
estimated standard deviation).
Rule 1: Variances add on addition or subtraction. For z = x ± y, (σ z ) 2 = (σ x ) 2 + (σ y ) 2
Rule 2: Relative variances add on multiplication or division. For z = x · y or z = x/y,
2
2
2
⎛ σ
⎛ σ ⎞
z ⎞ ⎛ σ
x ⎞ y
⎜ ⎟ = ⎜ ⎟ +
⎜
⎟
⎝ z ⎠ ⎝ x ⎠ ⎝ y ⎠
Rule 3: The variance in ln x is equal to the relative variance in x and the variance in log x
is the (relative variance in x)/(2.303) 2 .
⎛ σ
⎝ x
⎞
2
2 x
For z = ln x, ( σ
z
) = ⎜ ⎟ and for z = log x, since ln 10 = 2.303, ( σ
z
)
⎠
2
=
1
( ln10)
⎛ σ
x
⎜
⎝ x
Rule 4: The relative variance in e x is equal to the variance in x and the relative variance
in 10 x is equal to the (variance in x)(2.303) 2 .
⎛ σ ⎞
⎜ ⎟
⎝ z ⎠
2
For z = e x z
, ( ) 2
and for z = 10 x z
, = ( ln10) 2
( σ ) 2
=
σ
x
⎛ σ ⎞
⎜ ⎟
⎝ z ⎠
Rule 5: In calculations with only one error term, you can work with standard deviation
instead of variance.
Rule 6: The variance of an average of N numbers, each with variance σ 2 , is σ 2 /N. (The
standard deviation in the average improves as √(1/N)).
2
x
2
2
⎞
⎟
⎠
These rules all follow from the general formula from calculus for error propagation
e
2
F
2
⎛ ∂ F ⎞
= ⎜ ⎟
⎝ ∂ x ⎠
2
2 ⎛ ∂ F ⎞
ex
+ ⎜ ⎟
⎝ ∂ y ⎠
2
2 ⎛ ∂ F ⎞
e
y
+ ⎜ ⎟
⎝ ∂ z ⎠
e
2
z
K

where one is calculating some function F which depends upon experimental quantities x,
y, z, … which have random errors e x , e y , e z , … associated with them (see Appendix C).
These rules are also summarized in Table 3-1 of the text.
.
Example 5: Subtraction: If Z = A – B with A = 163.455 ± 0.002 and B = 1.34 ± 0.02
calculate Z. Find the uncertainty in the result.
Solution: Work with absolute variances (Rule 1) and note that variances always add (i.e.
the error always builds up):
[variance in A = (0.002) 2 ] + [variance in B = (0.02) 2 ]
variance in result (0.02) 2 => standard deviation = 0.02
Result: (163.455 ± 0.002) – (1.34 ± 0.02) = 162.12 ± 0.02
Example 6: Multiplication: The result of an experiment is given by (slope × Cp). Let
slope = 123.2 ± 2.4 and Cp = 4.184 ± 0.031. Find the uncertainty in the result.
Solution: The relative variance of the result is the sum of the relative variances of the
data (Rule 2).
[relative variance in slope = (2.4/123.2) 2 = (0.019 48 ) 2 = 3.7 94 × 10 -4 ]
+ [relative variance in Cp = (0.031/4.184) 2 = (0.0074 09 ) 2 = 5.4 89 × 10 -5 ]
relative variance in product = 4.3 43 × 10 -4
relative standard deviation in product = √(4.3 43 × 10 -4 ) = 0.020 84 or 2.0 84 %
Result: (123.2 ± 2.4) × (4.184 ± 0.031) = 515.4 68 ± 2.0 84 % = 515 ± 11

Example 7: Logs: The equilibrium constant for a reaction at two different temperatures
is K 1 = 0.0322 ± 0.0007 at 298.2 and K 2 =0.473 ± 0.006 at 353.2 K. Calculate ln(K 2 /K 1 )
and find the uncertainty in the result.
Solution: Just like Example 6 the relative variance in K 2 /K 1 is the sum of the relative
variances:
[relative variance in K 2 = (0.0007/0.0322) 2 = (0.02 17 ) 2 = 4. 72 × 10 -4 ]
+ [relative variance in K 1 = (0.006/0.473) 2 = (0.01 26 ) 2 = 1. 60 × 10 -4 ]
relative variance in K 2 /K 1 = 6. 33 × 10 -4
Using Rule 3 shows that absolute variance in ln K 2 /K 1 is the relative variance in K 2 /K 1 .
variance in ln K 2 /K 1 = relative variance in K 2 /K 1 = 6. 33 × 10 -4
standard deviation in result = √(6. 33 × 10 -4 ) = 0.02 51
Result: ln(K 2 /K 1 ) = ln 14.6 89 => 2.687 12 ± 0.02 51 = 2.69 ± 0.03
See Example 2 for the significant figure version of this error analysis.
Example 8: Antilogs: The rate of a reaction depends on temperature as ln k = ln A –
E a /RT. Using curve fitting it was found that ln A = 9.874 ± 0.041. Calculate A and find
the uncertainty.
Solution: The result is e 9.874 = 1.94 18 × 10 4 . The relative variance of the result is the
absolute variance of A (Rule 4):
relative variance of e 9.874 = variance of A = (0.041) 2 = 1.6 81 × 10 -3
relative standard deviation in result = √(1.6 81 × 10 -3 ) = 0.041 00 or 4.1 00 %
Result: 1.94 18 × 10 4 ± 4.1 00 % = (1.94 18 ± 0.079 61 ) × 10 4 = (1.94 ± 0.08) × 10 4
See Example 3 for the significant figure version of this error analysis.
Example 9: Multiplication with 'certain' numbers: The result of a calculation is (slope ×
R), where R is the gas constant in J K -1 mol -1 . Let slope = 1.23 ± 0.02. Find the
uncertainty in the result.
Solution: Since R is known to several more significant figures than the slope, the
uncertainty in R will add very little to the error in the final result. Therefore, R is 'certain'
for this calculation. Rule 5 applies since only the slope is in error. Therefore, the error in
the final result is then just the standard deviation in the slope multiplied by R:
Result: slope × R = 1.23 ± 0.02 × 8.31441 26 = 10.2 26 ± 0.1 66 = 10.2 ± 0.2
Example 10: The Inverse of the Slope or Intercept: The result of an experiment is the
inverse of the intercept from a graph, 1/b. Let b = 0.523 ± 0.043. Find the uncertainty in
the result.

Solution: The relative variance in the result is equal to the relative variance in the
intercept (Rule 2). We can also work directly in terms of standard deviation (Rule 5):
relative standard deviation in b = 0.043/0.523 = 0.082 21 or 8.2 21 %
relative standard deviation of result = relative standard deviation in b = 8.2 21 %
Result: 1/b = 1/0.523 = 1.91 20 ± 8.2 21 % = 1.91 20 ± 0.15 71 = 1.91 ± 0.16
Example 11: Division and Subtraction: The term (1/T 2 – 1/T 1 ) is a very common factor
in many equations. For T 1 = 298.2 ± 0.2 K and T 2 = 353.2 ± 0.2 K calculate (1/T 2 – 1/T 1 ).
Find the uncertainty in the result.
Solution: Do not be put off by multi-step problems, just work one step at a time. First,
get the uncertainty in 1/T 2 and 1/T 1 . Since both of these are divisions the relative variance
of 1/T is just the relative variance of T (Rule 2). Then convert to absolute variance to
calculate the error in (1/T 2 – 1/T 1 ) using Rule 1:
relative variance in T 2 = (0.2/353.2) 2 = 3. 20 × 10 -7
relative variance in T 1 = (0.2/298.2) 2 = 4. 49 ×10 -7
[variance in 1/T 2 = 3.2 × 10 -7 (1/353.2) 2 = 2. 57 × 10 -12 ]
+ [variance in 1/T 1 = 4.5 ×10 -7 (1/298.2) 2 = 5. 05 × 10 -12 ]
variance in (1/T 2 – 1/T 1 ) = 7. 62 × 10 -12
standard deviation in result = √(7. 62 × 10 -12 ) = 2. 76 × 10 -6
Result: -5.221 96 × 10 -4 ± 2. 76 × 10 -6 = (-5.22 ± 0.03) × 10 -4
Example 12: A Multi-Step Problem: An example of a more realistic problem is the
temperature dependence of the equilibrium constant. We wish to evaluate ΔH, knowing
K 1 , K 2 , R, T 1 , and T 2 in the equation:
ln(K 2 /K 1 ) = – ΔH/R (1/T 2 – 1/T 1 )
where K 1 = 0.0322 ± 0.0007 at 298.2 and K 2 = 0.473 ± 0.006 at 353.2 K with T = ± 0.2 K
(The same data as Examples 7 and 11). Find the uncertainty in the result.
Solution: Solving for ΔH: ΔH = – 8.31441[ln(K 2 /K 1 )]/(1/T 2 – 1/T 1 ) = 42.78 44 kJ/mol
We already know the uncertainty in ln(K 2 /K 1 ) from Example 7, 2.687 12 ± 0.02 51 , and the
uncertainty in (1/T 2 – 1/T 1 ) from Example 11, (-5.221 96 ± 0.02 76 ) × 10 -4 . R is a certain
number. The relative variance in ΔH is then just the sum of the relative variances:
relative variance ΔH = (0.02 51 /2.687 12 ) 2 + (0.02 76 × 10 -4 / 5.221 96 × 10 -4 ) 2 = 1.1 51 × 10 -4
relative standard deviation of ΔH = √(1.1 51 × 10 -4 ) = 0.010 73 or 1.0 73 %
standard deviation of ΔH = (0.010 73 )(42.78 44 ) = 0.45 91 kJ/mol
Result: ΔH = 42.78 ± 0.46 => 42.8 ± 0.5 kJ/mol