Lecture notes - School Of Electrical & Electronic Engineering - USM

Root Locus 

Bode Plot 

Example on Root Locus 

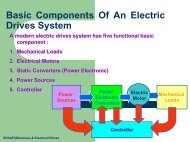
DIGITAL CONTROL SYSTEM 

EEE354 

Stability Analysis Techniques: root locus and bode diagram 

MUHAMMAD NASIRUDDIN MAHYUDDIN 

School of Electrical and Electronic Engineering, 

UNIVERSITI SAINS MALAYSIA 

week 10 

Semester II 2007/2008 

nasiruddin@eng.usm.my EEE 354 : STABILITY ANALYSIS TECHNIQUES

Outline 

Root Locus 

Bode Plot 


week 10: 18/02/2008 - 23/02/2008 

1 Root Locus 

overview 

general rules of Root Loci sketching 

2 Bode Plot 

Advantages of Bode Plot 

Sketching technique revisited 

Performance Specification 

example on frequency response analysis: bode plot 

3 Example on Root Locus 


Root Locus 

Bode Plot 


stability technique using root locus 

overview 


Generally, the CE for a digital system can be written as 

where, 

1 + F(z) = 0 

F(z) = G(z)H(z) or F(z) = GH(z) 

F(z) is the open-loop pulse transfer function of the discrete-time 

or digital system. Since F(z) is a complex quantity, it can be 

split into two equations: angles and magnitude. 


Root Locus 

Bode Plot 


stability technique using root locus 

overview 


a) Angle Criterion: 

b) Magnitude Criterion: 

∠F(z) = ±180 ◦ (2k + 1), k = 0, 1, 2, ... (1) 

|F(z)| = 1 (2) 

The values of z that satisfy both the angle and the mangitude 

criterions are the roots of characteristic equations. 


Root Locus 

Bode Plot 


Rules of sketching ROOT LOCI 

overview 


1 Obtain the characteristic equation or CE: 1 + F(z) 

2 Find the starting point(poles) : K = 0, (and the number of 

poles, n) 

3 Find the ending point(zeros) : K = ∞, (and the number of 

zeros, m) 

4 The number of end points at infinity : n − m 

5 Find the root loci on the real axis: Use the right test point 

method... 


Root Locus 

Bode Plot 



overview 


1 Determine the asymptotes: 

Angle of asymptotes: 

θ q = 

(2k + 1)π 

, k = 0, 1, 2, . . . , |n − m| − 1 (3) 

n − m 

Intersection of asymptotes with the real axis: 

σ 1 = 

∑ ∑ real parts of poles of F(z) − real parts of zeros of F(z) 

. ( 

n − m 


Root Locus 

Bode Plot 



overview 


1 Find the break-away and break-in points on the real axis, if 

any: 

1 + F(z) = 1 + KF 1 (z) = 0 

K = − 1 

F(z) 

(5) 

The break-away and break-in point can be determined 

from the roots of 

dK 

dz = − d 1 

dz F 1 (z) = 0 (6) 


Find the point(s) where the root loci cross the imaginary 

axis. 

It can be found by setting z = jω in CE. Then, equate both 

the real part and the imaginary part to zero, and solve for ω 

and K. ω is the point where the root loci cross the 

imaginary axis and K the corresponding gain at that 

cross-over nasiruddin@eng.usm.my point. 

EEE 354 : STABILITY ANALYSIS TECHNIQUES 

Root Locus 

Bode Plot 



overview 


Determine the angle of departure (or the angle of arrival) 

of the root locus from the complex poles (or at the complex 

zeros): 

Angle of arrival: 

(you may use the angle of criterion to derive this equation) 

φ = 180 ◦ [ ∑ 

∠(from all poles to φ) − 

∑ 

∠(from all zeros to φ) 

] 

(7

Root Locus 

Bode Plot 



overview 


The intersection of the root loci with the unit circle |z| = 1 

can be found by using the extended R-H or Jury’s stability 

test. 

The magnitude criterion enables us to determine the value 

of the gain K at any specific root location on the locus. The 

gain K can be found as follows: 

K = 

(z + p 1 )(z + p 2 ) . . . (z + p n ) 

∣ (z + z 1 )(z + z 2 ) . . . (z + z m ) ∣ (8) 

Given the value of the gain, the closed loop pole for that 

gain can also be found by using the same formula. 


exercise 

Root Locus 

Bode Plot 


overview 


do exercise 7-14 in Philip Nagle book 


example 

Root Locus 

Bode Plot 


overview 


do exercise 4-7 in Ogata Book. 

Draw the root locus diagrams in the z-plane for the system for 

the following three sampling periods: T=1 sec; T= 2 sec and T 

= 4 sec. 


Root Locus 

Bode Plot 







In the Bode diagram, the low frequency asymptote of the 

magnitude curve is indicative of one of the static error constants 

K p , K v , K a . 

Specifications of the transient response can be translated into 

those of frequency response in terms of the phase margin, gain 

margin, bandwidth, so forth. These can be easily handled in the 

bode diagram. 

The design of digital compensator to satisfy specifications can 

be carried out in the Bode diagram in a simple and 

straightforward manner 


Bode Plot 

Root Locus 

Bode Plot 






Before using the bode plot, the transfer function G(z) must first 

be converted into G(w ′ ) in w ′ domain by using the following 

bilinear transformation of equation 9 

z = 1 + T 2 w′ 

1 − T 2 w′ = 

2 

T + w′ 

2 

T − w′ (9) 

Since the Bode plot is a frequency domain analysis technique, 

G(jv ′ ) is obtained after the transform transfer function G(w ′ ) in 

w ′ -domain has beend determined by replacing w ′ with jv ′ . 


Bode Plot 

Root Locus 

Bode Plot 






The bode plot consists of two separate plots: 

a. The magnitude plots 

b. The phase plot 

Now, instead of using ω as an expression for frequency, we will 

use v ′ . This is called fictitious frequency. 

The magnitude |G(jv ′ )| is usually expressed in decibels (dB) i.e. 

20log 10 |G(jv ′ )|. The sketching techniques are the same as what 

you have learnt in EEE 350 whereby we plot each of the factors 

contribution in the bode plot and later, add all of these factors to 

form the complete plot of any given digital system transfer 

function. Yes, we still use asymptotic approximation in 

bode plot skteching. 


Root Locus 

Bode Plot 






The Magnitude and Phase plots for Factors in Bode 

plot 

Factor (jv ′ ) ±1 


Root Locus 

Bode Plot 







plot 

Factor (1 ± Ajv ′ ) 


Root Locus 

Bode Plot 







plot 

Factor (1 ± Ajv ′ ) −1 


Root Locus 

Bode Plot 







plot 

Factor (B + Ajv ′ + (jv ′ ) 2 ) ±1 


Bode plot 

Root Locus 

Bode Plot 






The overall magnitude versus frequency plot for the system can be 

obtained by graphically adding all the plots of the various factors 

present in the transfer function. 

This does applied for digital systems as mush as it does on 

continuous systems. 


Root Locus 

Bode Plot 







Relative stability of closed-loop systems can be judged based 

on two performance specification in the frequency domain: 

Gain Margin 

Phase Margin 


Root Locus 

Bode Plot 







Gain Margin: 

The gain margin is the number of dB that |G(jv ′ | is 

below 0 dB at the phase crossover frequency (phase 

angle φ of G(jv ′ ) = 180 ◦ . It can also be defined as the 

amount of the system gain that can be increase before 

the closed loop system becomes unstable. 

Phase Margin: The phase margin is the number of degrees the 

phase of |G(jv ′ | is above −180 ◦ at the gain crossover 

frequency (|G(jv ′ | = 1. It can also be defined as the 

angle where the phase can be increased before the 

closed loop system becomes unstable 


Root Locus 

Bode Plot 


Gain and Phase Margin 





The system is unstable if either the gain margin or the phase margin 

or both have a negative value as shown in Figure 1 

Figure 1: Gain and Phase Margin in bode diagram 


Root Locus 

Bode Plot 


Gain and Phase margin 





Stable and unstable system in Bode diagram are shown in 

Figure 2 

Figure 2: Gain and Phase Margin in bode diagram 


Example 

Root Locus 

Bode Plot 






Consider a system with the following transfer function as shown in Figure 3: 

Figure 3: System plant 

Assuming the input is a unit step function, calculate the following: 

1 The range of stability for gain K using Routh Hurwitz method. 

2 Verify the answer in part (a) by plotting bode plot for the system. 

3 Find the gain and phase margin for th system from the bode plot drawn. 


Root Locus 

Bode Plot 


Solution to the example 





G(z) can be calculated as follows: 

G(z) 

= ( z−1 

z 

) 

Z 

[ 

1 

s 2 (s+1) 

] 

T=1 

= z−1 

z 

[ ] 

z[(1−1+e −1 )z+(1−e −1 −e −1 )] 

(z−1) 2 (z−e −1 ) 

(10) 

= 0.368z+0.264 

z 2 −1.368z+0.368 


Root Locus 

Bode Plot 


cont. solution to example 





With the sampling time given as T = 1 sec, the characteristic 

equation can be written as, 

1 + KG(w) = 1 + KG(z)| z=(1+0.5w)/(1−0.5w) 

= 1 + 

K[0.368[ 1+0.5w +0.264]] 

1−0.5w 

[ 1−0.5w] 1+0.5w 2 −1.368[ 1−0.5w]+0.368 

1+0.5w 

(11) 


Root Locus 

Bode Plot 







1 + KG(w) = 1 + −0.0381K(w−2)(w+12.14) 

w(w+0.924) 

(12) 

= (1−0.0381K)w2 +(0.924−0.386K)w+0.924K 

w(w+0.924) 

The CE can be expressed as 

(1 − 0.0381K)w 2 + (0.924 − 0.386K)w + 0.924K = 0 


Root Locus 

Bode Plot 







The Routh Hurwitz can be then formed as 

w 2 1 − 0.0381K 0.924K⇒K < 26.2 

w 1 0.924 − 0.386K ⇒K < 2.39 

w 0 0.924K ⇒K > 0 

(13) 

Hence the system is stable for 0

Root Locus 

Bode Plot 







It is to remind that K = 2.39 is the critical gain or the gain which 

cause the system to be marginally stable. 

In a manner similar to that employed in continuous-time 

systems, the frequency of oscillation at K = 2.39 can be found 

from the w 2 row of the array. We may obtain the auxillary 

equation as such, 

(1 − 0.0381)w 2 + 0.924K| K=2.39 = 0.9089w 2 + 2.181 = 0 

or 

√ 

2.181 

w = ±j 

0.9089 = ±j1.549 


Root Locus 

Bode Plot 


cont. Solution to example 





Then, ω w = 1.549 and from the relation between fictitious 

frequency and real frequency, 

[ ] 

ω w = 2 ωT 

T 

tan 

2 = 2 1 arctan (1.549)(1) 

2 

= 1.32rad/s 

It is found that 1.32 rad/s is the real frequency at which the 

system will oscillate with K=2.39. 

You may try different values of sampling time and reanalyze the 

system. You would see that the dependency of the system 

stability on the sampling period. The degradation of stability 

with increasing T, is due to the delay introduced by the sampler 

and data hold. 


Root Locus 

Bode Plot 







Bode Diagram: a frequency response method to analyze 

system stability 

From equation 12, we would substitute G(w)| jωw and yield, 

G(jω w ) 

= −0.0381(jωw−2)(jωw+12.14 

jω w(jω w+0.924) 

= 

−(j 

ωw 

2 

(14) 

jωw 

−1)( +1) 

12.14 

ω w( jωw +1) 0.924 


Bode plot drawn 

Root Locus 

Bode Plot 






By inspection, we note that the break frequencies are ω w = 2 

and ω w = 12.14 and the denominator break frequencies are ω w 

= 0 and ω w = 0.924. Using what you have learnt in the previous 

subject Sistem Kawalan, use asymptotic approximation to draw 

your bode plot. Note the gain and phase margin. The final bode 

plot will look something like in Figure 4 


Bode plot drawn 

Root Locus 

Bode Plot 






Figure 4: The bode plot of the system 


Root Locus 

Bode Plot 



You may study the example on root locus for digital system from 

the book on the next slides 


Example on Root Locus

Example 2 on Root Locus

Lecture notes - School Of Electrical & Electronic Engineering - USM

Create successful ePaper yourself

Delete template?

Save as template?