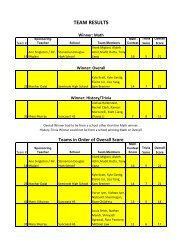
NAME: Calculus 3 Exam 1-September 18, 2012 Instructions ...
NAME: Calculus 3 Exam 1-September 18, 2012 Instructions ...
NAME: Calculus 3 Exam 1-September 18, 2012 Instructions ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>NAME</strong>:<br />
<strong>Calculus</strong> 3<br />
<strong>Exam</strong> 1-<strong>September</strong> <strong>18</strong>, <strong>2012</strong><br />
<strong>Instructions</strong>.<br />
• SHOW WORK! and write clearly. Show all work, answers obtained apparently by divine inspiration<br />
may get no credit.<br />
• Try to write in the form of full sentences. I may penalize you for the failure to use full sentences. A sentence<br />
must contain a verb. For example “5” or “x 2 +y 2 are NOT sentences. “x 2 +y 2 = 5” is a sentence; the symbol<br />
“=” would be read “is equal,” and “is” is a verb. Failure to use an equal symbol where it should be used will<br />
probably result in the loss of points.<br />
• Do not use an equal symbol to connect quantities that are not equal, except when setting up equations.<br />
Incorrect use of an equal symbol will result in loss of points.<br />
• Use extra paper as necessary.<br />
The Test.<br />
1. (5 points) Find the center and radius of the sphere of equation<br />
x 2 + y 2 + z 2 − 8x + 2y + 6z + 1 = 0.<br />
Solution.<br />
Completing the squares one gets<br />
The center is at (4, −1, −3), the radius is 5.<br />
(x − 4) 2 + (y + 1) 2 + (z + 3) 2 = 25.<br />
2. (5 points) If u and v are vectors as shown in the picture, find u · v and u × v. Is u × v directed into the<br />
page or out of it?<br />
u · v = |u| |v| cos(30 ◦ ) = 30 √ 3.<br />
This answers the question about u·v. Concerning<br />
the cross product,<br />
|u × v| = |u| |v| sin(30 ◦ ) = 30.<br />
But u × v is a vector, so we are not<br />
done yet. Since u, v, u × v have to<br />
form a right system we can say that<br />
u × v is a vector of length 30, pointing perpendicularly<br />
out from the page.
2<br />
3. Find parametric equations of the following lines.<br />
(a) (5 points) The line through the points (1, 0, −1) and (2, −3, 1).<br />
Solution. A direction vector for this line is given by a = 〈2 − 1, −3 − 0, 1 − (−1)〉 = 〈1, −3, 2〉. From<br />
this we can get the equations at once.Using the first point as base,<br />
x = 1 + t, y = −3t, z = −1 + 2t.<br />
(b) (10 points) The line through (2, −1, 0) and perpendicular to the plane of equation 5x + 2y − 3z = 6.<br />
At what point does this line intersect the plane?<br />
Solution. If the line is perpendicular to a plane, then a vector normal to the plane directs it. The<br />
obvious vector normal to the plane in question is 〈5, 2, −3〉. Parametric equations are<br />
x = 2 + 5t, y = −1 + 2t, z = −3t.<br />
The line intersects the plane for t such that 5(2 + 5t) + 2(−1 + 2t) − 3(−3t) = 6. Solving for t we get<br />
t = −1/19. Using this value for t we get the point (33/19, −21/19, 3/19).<br />
4. (10 points) Find the equation of the plane through the points (2, 1, 1), (−1, −1, 10), and (1, 3, −4).<br />
Solution.<br />
Taking the point of coordinates (2, 1, 1, ) as the base point, the plane is parallel to the vectors<br />
v = 〈−3, −2, 9〉 and w = 〈−1, 2, −5〉.<br />
Taking their cross product to get a vector normal to the plane:<br />
i j k<br />
n =<br />
−3 −2 9<br />
= −8i − 24j − 8k.<br />
∣ −1 2 −5 ∣<br />
An acceptable, though sort of ugly, answer is −8(x − 2) − 24(y − 1) − 8(z − 1) = 0. We could multiply by<br />
1 to get rid of the negative numbers. Or we can expand and rearrange to get 8x + 24y + 8z = 48 (also an<br />
acceptable answer); dividing by 8,<br />
x + 3y + z = 6.<br />
If I were a student in this course, after finding the equation of the plane, I would check that it<br />
works; that the given points satisfy it. If one of them didn’t, I would check my computations.<br />
Of course, that’s me.<br />
5. (5 points) Show that the points A(1, 1, 1), B(2, 6, −1), C(4, 0, 1), D(6, 10, −3) are coplanar, and find a fifth<br />
point in the same plane.<br />
Solution. One way of seeing the points are coplanar is to take one of them as a base, construct the three<br />
vectors starting at that point and ending at the other points, and verify that their triple product is 0. Taking<br />
A as base, the vectors are<br />
−→<br />
AB = 〈1, 5, −2〉,<br />
−→<br />
AC = 〈3, −1, 0〉, −→ AD = 〈5, 9, −4〉.<br />
The triple product works out to<br />
1 5 −2<br />
3 −1 0<br />
= 1((−1)(−4) − 0) − 5(3(−4) − 0) − 2((3)(9) − (−1)(5)) = 4 + 60 − 64 = 0.<br />
∣ 5 9 −4 ∣<br />
The triple product being 0, the points are coplanar. There are several ways of finding a fifth point. Here are<br />
two ways.<br />
Method 1. Any combination of the vectors −→ −→ −→<br />
−→ −→ −→<br />
AB, AC, AD with scalars (aAB + bAC + cAD where a, b, c<br />
are constants) will give a vector that starts at the point A and ends at a point of the plane. Adding<br />
the components of A to it will give a point of the plane. And we don’t even need to use all three of<br />
the vectors. For example, 2 −→ AB = 〈2, 10, −4〉 lies entirely in the plane if we start it at A; adding the<br />
components of A we get (3, 11, −3) as a fifth point in the plane.
3<br />
Method 2. Find the equation of the plane; then use it to give arbitrary values to two of the variables and<br />
solve for the third. To find the equation of the plane we take two of the vectors, for example −→ −→ AB, AC<br />
and form their cross product to get a vector normal to the plane.<br />
i j k<br />
n =<br />
1 5 −2<br />
= −2i − 6j − 16k.<br />
∣ 3 −1 0 ∣<br />
From this the equation of the plane works out to −2(x−1)−6(y −1)−16(z −1) = 0 or x+3y +8z = 12.<br />
Taking for example y = z = 0, we get x = 12. So a fifth point is (12, 0, 0) .<br />
6. Consider the curve given parametrically by x = sin 2t, y = t, z = cos 2t.<br />
(a) (10 points) Find the tangent, normal and binormal vectors (T(t), N(t), B(t)).<br />
Solution. The position function for this curve is<br />
r(t) = 〈sin 2t, t, cos 2t〉.<br />
Thus r ′ (t) = 〈2 cos 2t, 1, −2 sin 2t〉, |r ′ (t)| = √ 4 cos 2 2t + 1 2 + 4 sin 2 2t = √ 5. Thus<br />
Next, N(t) = (1/|T ′ (t)|)T ′ (t);<br />
T(t) = 1<br />
|r ′ (t)| r′ (t) = 1 √<br />
5<br />
〈2 cos 2t, 1, −2 sin 2t〉.<br />
T ′ (t) = √ 1 〈−4 sin 2t, 0, −4 cos 2t〉, |T ′ (t)| = 1 √ 5<br />
√16 sin 2 2t + 16 cos 2 2t = √ 4 .<br />
5 5<br />
Thus<br />
Finally<br />
B(t) = T(t) × N(t) =<br />
∣<br />
N(t) = 〈− sin 2t, 0, − cos 2t〉.<br />
i j k<br />
2√<br />
5<br />
cos 2t √5 1<br />
− √ 2 5<br />
sin 2t<br />
− sin 2t 0 − cos 2t<br />
∣ = − √ 1 cos 2ti + √ 2 j + √ 1 sin 2tk.<br />
5 5 5<br />
Thus (to keep the notation consistent)<br />
B(t) = 〈− 1 √<br />
5<br />
cos 2t,<br />
2<br />
√<br />
5<br />
,<br />
1<br />
√<br />
5<br />
sin 2t〉.<br />
(b) (5 points) Find an equation for the osculating plane at the point where t = π/4.<br />
Solution. The osculating plane is normal to the binormal vector. At π/4 the binormal vector is<br />
〈0, 2/ √ 5, 1/ √ 5〉. Since any vector parallel to the binormal will do, we can multiply by √ 5 and use<br />
n = 〈0, 2, 1〉. The point on the curve corresponding to t = π/4 is (1, π/4, 0). Putting it all together, the<br />
equation for the osculating plane works out to 2(y − π/4) + z = 0 or<br />
2y + z = π 2 .<br />
7. (10 points) A particle starts from the origin with velocity v 0 = i + 3j − 4k. Its acceleration as a function of<br />
time is given by a(t) = −3t 2 i + 4tj + 4t 3 k. Determine its position function r(t).<br />
Solution.<br />
The velocity of the particle is given by<br />
∫ ∫<br />
v(t) = a(t) dt = (−3t 2 i + 4tj + 4t 3 k) dt = −t 3 i + 2t 2 j + t 4 k + c.<br />
Setting t = 0, mv(0) = v 0 we see that c = v 0 = i + 3j − 4k so that<br />
v(t) = (−t 3 + 1)i + (2t 2 + 3)j + (t 4 − 4)k.
4<br />
Now<br />
∫<br />
r(t) =<br />
∫<br />
v(t) dt =<br />
[(−t 3 + 1)i + (2t 2 + 3)j + (t 4 − 4)k] dt = (− 1 4 t4 + t)i + ( 2 3 t3 + 3t)j + ( 1 5 t5 − 4t)k + c.<br />
Setting t = 0 we should have r(0) = 0; this gives c = 0. The answer is<br />
(− 1 4 t4 + t)i + ( 2 3 t3 + 3t)j + ( 1 5 t5 − 4t)k.<br />
8. The position vector of a particle is given by<br />
r(t) = 〈3t 2 , 3t 4 , 2t 6 〉.<br />
Suppose t is measured in seconds and distance is measured in meters. The particle starts at time t = 0<br />
(a) (5 points) Where is the particle at time t = 1 second?<br />
Solution. At (3, 3, 2).<br />
(b) (10 points) What distance has it travelled (measured along the trajectory!) at time t = 1?<br />
Solution.<br />
the distance will be given by<br />
s(1) =<br />
∫ 1<br />
0<br />
|r ′ (t)| dt =<br />
∫ 1<br />
0<br />
√<br />
36t2 + 144t 6 + 144t 1 0 dt.<br />
Here is where the hint can be helpful. Or having done some of the textbook exercise, where this situation<br />
happens several times. 36t 2 + 144t 6 + 144t 1 0 = (6t + 12t 5 ) 2 . So we have<br />
The distance equal 5 meters.<br />
s(1) =<br />
∫ 1<br />
0<br />
∣ ∣∣∣<br />
1<br />
(6t + 12t 5 ) dt = 3t 2 + 2t 6 = 5.<br />
(c) (10 points) At what time will it have travelled half the distance it travelled from time t = 0 to time<br />
t = 1? In other words, in part b, you found a certain distance s. The question now is: For what value<br />
of t is the distance s/2?<br />
Solution. If t is that time, we should have<br />
For t such that 3t 2 + 2t 6 = 2.5.<br />
∫<br />
5<br />
t<br />
∣ ∣∣∣<br />
t<br />
2 = s(t) = (6u + 12u 5 ) du = 3u 2 + 2u 6 = 3t 2 + 2t 6 .<br />
0<br />
0<br />
0<br />
Hint: If you are careful with the computations, don’t do anything foolish, any quantity that you have inside<br />
a square root should be a perfect square. Look at it carefully.
5<br />
9. (10 points) At what point does the curve y = e x have maximum curvature. Justify that the curvature<br />
is indeed maximum at that point. In case you forgot to add the formula for curvature of a curve given<br />
by y = f(x) to your “cheat sheet,”, here it is:<br />
κ(x) =<br />
By the given formula, the curvature works out to<br />
κ(x) =<br />
|f ′′ (x)|<br />
(1 + (f ′ (x)) 2 ) 3/2 .<br />
e x<br />
(1 + e 2x ) 3/2 .<br />
Using <strong>Calculus</strong> techniques, we find the derivative and set it to 0. We get (after some simplifying)<br />
κ ′ (x) = ex (1 − 2e 2x )<br />
(1 + e 2x ) 5/2 .<br />
There is only one zero, only one critical point, the value of x for which 2e 2x = 1; that is, x = (1/2) ln(1/2) =<br />
− ln 2/2. Noticing that if x < (1/2) ln(1/2) we have κ ′ (x) > 0, and κ ′ (x) < 0 for x > (1/2) ln(1/2), proves<br />
that we have a maximum. Answer: At x = − 1 ln 2.<br />
2