Solutions to Final Examination
Solutions to Final Examination
Solutions to Final Examination
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
EE32a Signals, Systems, and Transforms<br />
December 15, 2001<br />
<strong>Final</strong> <strong>Examination</strong> — <strong>Solutions</strong><br />
R. J. McEliece<br />
162 Moore<br />
Problem 1. (Graded by Muhammed) The first step is <strong>to</strong> decompose X(s) in<strong>to</strong> partial<br />
fractions:<br />
s − 1<br />
(s + 2)(s + 3)(s 2 + s +1) = −1<br />
s +2 + 4/7 (3s +1)/7<br />
+<br />
s +3 s 2 + s +1<br />
= X 1 (s)+X 2 (s)+X 3 (s).<br />
Note that the poles of X(s) are at s = −2, −3, and −1/2 ± j √ 3/2.<br />
The inverse Laplace transforms of X 1 (s), X 2 (s), and X 3 (s) are<br />
{<br />
x<br />
R<br />
x 1 (t) = 1 (t) =−e −2t u(t) Re(s) > −2<br />
x L 1 (t) =e −2t u(−t) Re(s) < −2<br />
{<br />
x<br />
R<br />
x 2 (t) = 2 (t) =(4/7)e −3t u(t) Re(s) > −3<br />
x L 2 (t) =−(4/7)e −3t u(−t) Re(s) > −3<br />
(<br />
x<br />
R<br />
x 3 (t) ={<br />
3 (t) = 1 7 3e −t/2 cos( √ 3t/2) − (1/ √ 3)e −t/2 sin( √ 3t/2) ) u(t) Re(s) > −1/2<br />
(<br />
x L 3 (t) =− 1 7 3e −t/2 cos( √ 3t/2) − (1/ √ 3)e −t/2 sin( √ 3t/2) ) u(−t) Re(s) < −1/2<br />
.<br />
The four inverse Laplace transforms of the original X(s) are then<br />
Re(s) < −3 :x L 1 (t)+x L 2 (t)+x L 3 (t)<br />
−3 < Re(s) < −2 :x L 1 (t)+x R 2 (t)+x L 3 (t)<br />
−2 < Re(s) < −1/2 :x R 1 (t)+x R 2 (t)+x L 3 (t)<br />
Re(s) > −1/2 :x R 1 (t)+x R 2 (t)+x R 3 (t)<br />
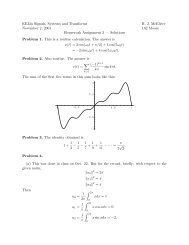
-2 -1.5 -1<br />
-10<br />
-20<br />
-30<br />
-40<br />
-50<br />
x(t), Re(s) < −3.<br />
1
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
-1 -0.5 0.5 1<br />
x(t), −3 < Re(s) < −2.<br />
2<br />
-8 -6 -4 2<br />
-2<br />
-4<br />
-6<br />
x(t), −2 < Re(s) < −1/2.<br />
2
0.04<br />
0.02<br />
-0.02<br />
2 4 6 8 10<br />
-0.04<br />
-0.06<br />
-0.08<br />
x(t), Re(s) > −1/2.<br />
3
Problem 2. (Graded by all.)<br />
(a) Use the fact that Re x(t) =(x(t)+x ∗ (t))/2, and entry 4.3.3 in Table 4.1, p. 328:<br />
Re x(t) ←→ F X(jΩ) + X∗ (−jΩ)<br />
.<br />
2<br />
(b) Using entries 4.3.3 and 4.3.5 in Table 4.1 :<br />
x ∗ (−t) F<br />
←→X ∗ (jΩ).<br />
(c) Using the given decomposition and entry 4.3.5 in Table 4.1 :<br />
Ev x(t) ←→ F X(jΩ) + X(−jΩ)<br />
.<br />
2<br />
4
Problem 3. (Graded by RJM) The key <strong>to</strong> this problem is <strong>to</strong> use z-transforms. Indeed, if<br />
g[n] ∗ g[n] =h[n], we have<br />
G(z) 2 = H(z).<br />
Thus if g[n] isaconvolution square root of h[n], we have<br />
G(z) =± √ H(z).<br />
(a) Here H(z) =1+2z −1 + z −2 =(1+z −1 ) 2 ,soG(z) =±(1 + z −1 ) 2 . Ignoring the<br />
possible minus sign, we have<br />
{ 1 if n =0orn =1<br />
g[n] =<br />
0 otherwise.<br />
(b) Here we have<br />
H(z) = ∑ n≥0(n +1)z −n =<br />
1<br />
(1 − z −1 ) 2 .<br />
Thus G(z) =1/(1 − z −1 ), so that (again ignoring the possible minus sign)<br />
h[n] =u[n].<br />
(c) Here H(z) = ∑ n≥0 z−1 =1/(1 − z −1 ), so that G(z) =(1− z −1 ) −1/2 . But as we<br />
discussed in class on Nov. 9, we can apply the binomial theorem, even when the exponent<br />
is negative, so that<br />
g(z) =(1− z −1 ) −1/2 = ∑ ( ) −1/2<br />
(−1) n z −n .<br />
n<br />
n≥0<br />
Thus<br />
( ) −1/2<br />
g[n] =(−1) n u[n].<br />
n<br />
This expression can be simplified considerably.:<br />
(−1) n ( −1/2<br />
n<br />
Thus g[0] = 1, and for n ≥ 1,<br />
)<br />
=(−1) n · (− 1 2 )(− 3 2n−1<br />
2<br />
) ···(−<br />
2<br />
)<br />
1 · 2 ···n<br />
=( 1 2 ) · (3 4 ) ···(2n − 1<br />
2n ).<br />
n∏<br />
(<br />
g[n] = 1 − 1 )<br />
.<br />
2k<br />
k=1<br />
For example g[1] = 1/2, g[2] = 3/8, g[3] = 5/16, etc.<br />
Notess: A few studeents used Mathematica <strong>to</strong> find the inverse z-transform of G(z), and<br />
obtained the remarkable expression<br />
Γ(n +1/2)<br />
g[n] =<br />
Γ(n +1) √ π .<br />
I reluctantly accepted this formula. Also, some students found a recursive method for<br />
computing the sequence of g[n]’s. I <strong>to</strong>ok off 2.5 points for this approach.<br />
5
Problem 4. (Graded by Donald) This system in the serial iterconnection of two simpler<br />
systems, with systems functions (obtained by “inspection,” perhaps)<br />
H 1 (D) = 1 − 1 2 D<br />
1 − 1 3 D<br />
H 2 (D) =<br />
1<br />
4 + D<br />
1+ 1 2 D ,<br />
where I have substituted the delay opera<strong>to</strong>r D for the cumbersome z −1 . Thsu the overall<br />
system function is<br />
1<br />
4<br />
H(D) =H 1 (D)H 2 (D) =<br />
+ 7 8 D − 1 2 D2<br />
1+ 1 6 D − 1 .<br />
6 D2<br />
from this we can read off the difference equation. It is<br />
(a) y[n]+ 1 6 y[n − 1] − 1 6 y[n − 2] = 1 4 x[n]+7 8 x[n − 1] − 1 x[n − 2].<br />
2<br />
Of course the frequency responce is just the systems function evaluated at z = e jΩ :<br />
(b) H(e jΩ )=<br />
1<br />
4 + 7 8 e−jΩ − 1 2 e−2jΩ<br />
1+ 1 6 e−jΩ − 1 6 e−2jΩ .<br />
<strong>Final</strong>ly, <strong>to</strong> obtain the impulse response, we first decompose the expression for H(z) in<strong>to</strong><br />
partial fractions:<br />
13<br />
21<br />
20<br />
H(D) =3−<br />
1 − 1 3 D − 10<br />
1+ 1 2 D .<br />
The impulse response h[n] isjust the coefficient of D n in the expansion of H(D) asapower<br />
series in D, and so:<br />
(c) h[n] =3δ[n] − 13<br />
20 (1 3 )n − 21<br />
10 (−1 2 )n ,<br />
for n ≥ 0.<br />
6
Problem 5. (Graded by Cedric)<br />
(a) The easy way <strong>to</strong> do this problem is <strong>to</strong> observe that “the triangle is the convolution<br />
of the box with itself,” i.e.,<br />
x(t) =y(t) ∗ y(t),<br />
where<br />
y(t) =<br />
{<br />
1 if |t| ≤1/2<br />
0 if |t| > 1/2.<br />
Using the result of Example 4.4 (or Table 4.2), we have<br />
Y (jω)=2<br />
sin ω/2<br />
,<br />
ω<br />
so that<br />
X(jω)=Y (jω) 2 =4 sin2 ω/2<br />
ω 2 .<br />
(b)<br />
1<br />
-5 -4 -3 -2 --1 1 2 3 4<br />
Sketch of x(t) ∗ ∑ +∞<br />
k=−∞<br />
δ(t − 4k).<br />
(c) Here are two such g(t)’s (there are infinitely many more):<br />
7
1<br />
-5 -4 -3 -2 --1 0 1 2 3 4<br />
1<br />
-5 -4 -3 -2 --1 0 1 2 3 4<br />
8