- Page 2 and 3: Computational Accelerator Physics 2
- Page 4 and 5: Other titles in the series The Inst
- Page 6 and 7: viii AHF booster tracking with SIMP
- Page 8 and 9: Copyright ©2004 by IOP Publishing
- Page 10 and 11: £ 0 ¥ 0 ¥ 2 g plane as, e.
- Page 12 and 13: ¥ G ¥ G ¥ 4 With given 7 ¤2
- Page 14 and 15: § § § § § § ¥ ¥ ¥ ¥
- Page 16 and 17: $ ¥ ¥ ¢¡¤£ ¢ ¤27,94:
- Page 18 and 19: 10 By 0.1 µ 0 My 0.06 0 0.04 0.02
- Page 22 and 23: 14 has to communicate with a suitab
- Page 24 and 25: 16 These procedures use only forwar
- Page 26 and 27: 18 5. The parallel force decomposit
- Page 28 and 29: 20 Here the i and j are local indic
- Page 30 and 31: 22 6. Parallel force decomposition
- Page 32 and 33: 24 ST Accel. Beams 5, 024401 (2002)
- Page 34 and 35: 26 numerical PIC solutions are exte
- Page 36 and 37: 28 3.1. Initial distribution We fir
- Page 38 and 39: 30 2 2 2 ε ε ε 1 0 s 1000 1 0 s
- Page 40 and 41: 32 still to a KV beam the equations
- Page 42 and 43: 34 7. 3D model and its applications
- Page 45 and 46: Inst. Phys. Conf. Ser. No 175 Paper
- Page 47 and 48: 39 complicated enough to need more
- Page 49 and 50: 41 at the beginning of the name to
- Page 51 and 52: 43 7. Array access To access arrays
- Page 53: [10] M. Berz. Differential algebra
- Page 56 and 57: 48 either accomplished by computing
- Page 58 and 59: 50 emitted from a perfect conductor
- Page 60 and 61: 52 retardation effects with the cat
- Page 62 and 63: 54 Table 1. Transverse emittance an
- Page 64 and 65: 56 Recommendation 2. Devise abstrac
- Page 66 and 67: 58 Component Correction (JOCC) proc
- Page 68 and 69: 60 so there is some motivation to c
- Page 70 and 71:
62 Figure 3. Electric field magnitu
- Page 72 and 73:
64 conditional stability of FDTD me
- Page 74 and 75:
66 2.2. One-step algorithm The basi
- Page 76 and 77:
68 We immediately see that H is spa
- Page 78 and 79:
70 2 0 log (error) -2 -4 -6 Yee U2(
- Page 80 and 81:
72 References [1] M. Born and E. Wo
- Page 82 and 83:
74 2.A brief introduction to Geant4
- Page 84 and 85:
76 • The BTSheet class inherits f
- Page 86 and 87:
78 • The BTrfWindowLogicVol class
- Page 88 and 89:
80 Figure 3. Left: cooling unit cel
- Page 90 and 91:
82 References [1] See Geant4home pa
- Page 92 and 93:
84 phase space to the transverse(ho
- Page 94 and 95:
86 ε nx (m*rad) ε ny (m*rad) z (m
- Page 96 and 97:
88 10 β (m) β β @ 0 0 4 8 1 2 1
- Page 98 and 99:
90 Table 2. Parameters of an 8 cell
- Page 100 and 101:
92 Figure 1. Code compendium websit
- Page 102 and 103:
94 Radial Motion in Ion Linear Acce
- Page 104 and 105:
96 accelerating structures in the s
- Page 106 and 107:
98 and will facilitate the eventual
- Page 108 and 109:
100 MARYLIE Collaboration - MARYLIE
- Page 110 and 111:
102 used to create a 200 fs electro
- Page 112 and 113:
104 Because not all external fields
- Page 114 and 115:
106 As shown in Figure 4, the dimen
- Page 116 and 117:
108 75 8 7 Bunch length [m] 70 65 6
- Page 118 and 119:
110 The accuracy, speed and applica
- Page 120 and 121:
112 Two typical assumptions are the
- Page 122 and 123:
114 Our S-parameter calculations we
- Page 124 and 125:
116 This can be provided either by
- Page 126 and 127:
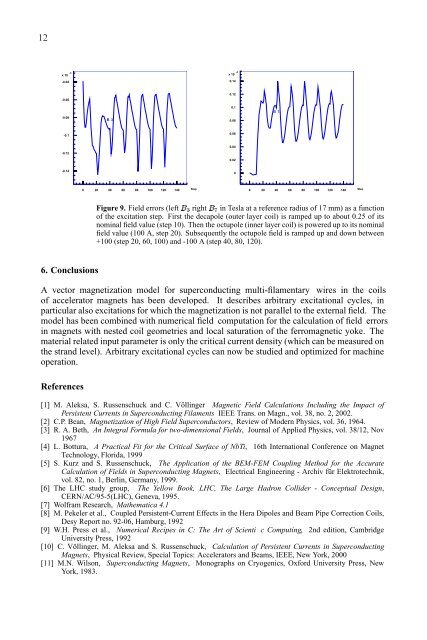
118 Figure 9. Difference of field o
- Page 128 and 129:
120 Introducing a nonvanishing angu
- Page 130 and 131:
122 Figure 1. AHF Booster Lattice F
- Page 132 and 133:
124 Table 3. 4” Booster Dipole er
- Page 134 and 135:
126 In the simulation, 20,335 macro
- Page 136 and 137:
128 Figure 5. B9L Beam parameters D
- Page 138 and 139:
130 The green cross indicates the i
- Page 140 and 141:
132 2.1. Two dimensions For the str
- Page 142 and 143:
134 0.06 interpolated grid solution
- Page 144 and 145:
136 Table 2. Pool algorithm: 2.5 ·
- Page 146 and 147:
138 Acausal particles need to skip
- Page 148 and 149:
140 0.014 0.012 0.01 turns/s/proces
- Page 151 and 152:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 153 and 154:
145 • calculate the linear transf
- Page 155 and 156:
147 N L 70 60 50 40 30 20 10 70 60
- Page 157:
149 tracking simulation of ≈ 10 1
- Page 160 and 161:
152 The Ensemble Model [1,2] repres
- Page 162 and 163:
154 with mean velocities v0 and th
- Page 164 and 165:
156 where Rr r , - rms ellips
- Page 166 and 167:
158 T 1/2 Tˆ ˆ ˆ ˆ ; ˆ 0
- Page 168 and 169:
160 The results are in very good ag
- Page 170 and 171:
162 GEANT [4], PENELOPE [5] for sim
- Page 172 and 173:
164 processing and comparative anal
- Page 174 and 175:
166 A scheme of grouping of collisi
- Page 176 and 177:
168 Regimes of irradiation: one- a
- Page 179 and 180:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 181 and 182:
173 In addition, a Position Start D
- Page 183 and 184:
175 ZGOUBI and tracked through the
- Page 185 and 186:
177 3. Magnetic field reconstructio
- Page 187 and 188:
179 Figure 6. Space distribution of
- Page 189 and 190:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 191 and 192:
183 design is that we can achieve a
- Page 193 and 194:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 195 and 196:
187 coordinates for the third order
- Page 197 and 198:
189 For electrostatic round lenses
- Page 199 and 200:
191 Table 1. Relationships between
- Page 201 and 202:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 203 and 204:
195 • because of Relativity, the
- Page 205 and 206:
197 their K/P slices before collaps
- Page 207 and 208:
199 Figure 5. Solving with perfectl
- Page 209:
201 A better solution may be found
- Page 212 and 213:
204 Beam intensity at wire (1/mm) 0
- Page 214 and 215:
206 histogram log QSCANFIT get exp.
- Page 216 and 217:
208 0.30 0.25 Beam intensity at wir
- Page 218 and 219:
210 Table 2. Invariant kurtosis for
- Page 220 and 221:
212 10.5 cm 198 cm 272 cm 198 cm R
- Page 222 and 223:
214 3 2 1 Bz (T) 0 -1 -2 -3 -2 -1 0
- Page 224 and 225:
216 6 5 4 Bz (T) 3 2 1 0 -2 0 2 4 6
- Page 226 and 227:
218 consideration; again the left p
- Page 228 and 229:
220 2. DA fixed point PDE solvers T
- Page 230 and 231:
222 • The method works to any ord
- Page 232 and 233:
224 -2 -1 0 1 2 3 s (m) CMSI R1 CMS
- Page 234 and 235:
226 The thinner case of CMST with R
- Page 236 and 237:
228 of position s. By using the tec
- Page 238 and 239:
230 Figure 1. Storage ring optics f
- Page 240 and 241:
232 (IDL). The latter feature is of
- Page 243 and 244:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 245 and 246:
237 the cartesian basis, the electr
- Page 247 and 248:
239 relative transit time error 10
- Page 249 and 250:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 251 and 252:
243 focusing. A particular configur
- Page 253 and 254:
245 Figure 1. A schematic view of a
- Page 255 and 256:
247 Figure 5. On the left a 4-sided
- Page 257 and 258:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 259 and 260:
251 2 2 r ( ) const a ( 0 ) . The
- Page 261 and 262:
253 Figure 3. Normalized spectrum o
- Page 263 and 264:
255 Corresponding phase photos (hig
- Page 265 and 266:
257 In the intermediate case when t
- Page 267 and 268:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 269 and 270:
261 signals is shown in figure 2. T
- Page 271 and 272:
263 Figure 5. Monopole 4.75 GHz mag
- Page 273 and 274:
265 6. Coupling studies Figure 9. D
- Page 275 and 276:
267 Monopole mode coupling is not c
- Page 277 and 278:
269 Figure 15. Dipole mode frequenc
- Page 279 and 280:
271 We make the assumption that all
- Page 281 and 282:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 283 and 284:
275 motions; analytical representat
- Page 285 and 286:
277 Figure 3. Cell length variation
- Page 287 and 288:
279 Figure 9. Emittance of beam at
- Page 289 and 290:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 291 and 292:
283 Strictly following this rule th
- Page 293 and 294:
285 3. Numerical test cases The new
- Page 295 and 296:
287 error of the electric field 0.3
- Page 297 and 298:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 299 and 300:
291
- Page 301 and 302:
293
- Page 303 and 304:
295
- Page 305 and 306:
297 20000 15000 Simulation two side
- Page 307 and 308:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 309 and 310:
301
- Page 311 and 312:
303
- Page 313 and 314:
305
- Page 315 and 316:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 317 and 318:
309 used. The actual charge distrib
- Page 319 and 320:
311 4.2. The 3D Space Charge class
- Page 321 and 322:
313 where the parameters 3 , 4 ,
- Page 323 and 324:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 325 and 326:
317
- Page 327 and 328:
319
- Page 329 and 330:
321
- Page 331:
323
- Page 334 and 335:
326
- Page 336 and 337:
328
- Page 338 and 339:
330
- Page 341 and 342:
Inst. Phys. Conf. Ser. No 175 Paper
- Page 343 and 344:
335 using infinitesimal calculus to
- Page 345 and 346:
337 Figure 1. Snapshot of the beam
- Page 347 and 348:
339 Figure 5. Snapshots of a) curre
- Page 349:
Figure 7. Left: phase-space project
- Page 352 and 353:
344 domain with the velocity of li
- Page 354 and 355:
346 When a bunch moves along the ax
- Page 356 and 357:
348 blocks. Each block is a three-b
- Page 358 and 359:
350 7. Numerical examples The confo
- Page 360 and 361:
352 r / cm 500 400 300 200 100 30 :
- Page 362:
354 Neuffer D 241 Shchepunov V 171