Version One – Homework 1 – Juyang Huang – 24018 – Jan 16 ...

Version One – Homework 1 – Juyang Huang – 24018 – Jan 16, 2008 24
as in Part 1.
The electric field for r < R with the
E =
Q
4 π ɛ 0 r 2 , where R < r , (1) = k Q r ,
R3 where R < r . (3)
sphere conducting: In the region inside The electric field for r < R with the
the conducting sphere, we select a spherical sphere uniformly non-conducting: In
gaussian surface r < R, concentric with the this case we select a spherical gaussian surface
conducting sphere. To apply Gauss’s law
at a radius r where r < R, concentric
in this situation, we realize that there is no with the uniformly charged non-conducting
charge within the gaussian surface (q in = 0), sphere. Let us denote the volume of this
which implies that
sphere by V ′ . To apply Gauss’s law in this
E = 0 , where r < R . (2)
situation, it is important to recognize that the
charge q in within the gaussian surface of the
E ∝ 1 volume V ′ is less than Q. Using the volume
r 2
charge density ρ ≡ Q
E
V , we calculate q in :
Y.
q in = ρ V
( ′
) 4
0 R
r
= ρ
3 π r3 .
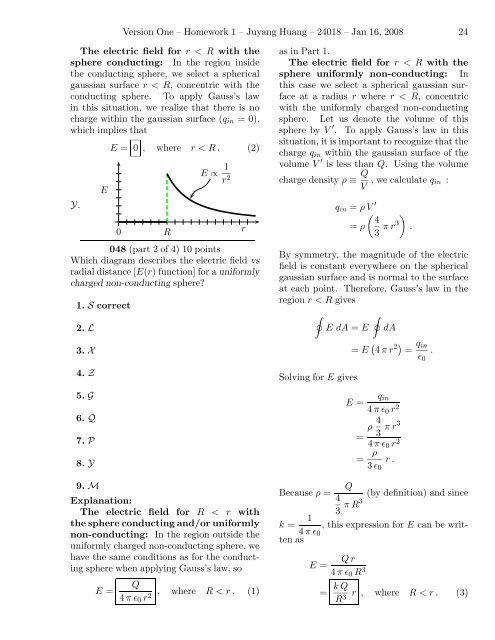
048 (part 2 of 4) 10 points
By symmetry, the magnitude of the electric
Which diagram describes the electric field vs
field is constant everywhere on the spherical
radial distance [E(r) function] for a uniformly
gaussian surface and is normal to the surface
charged non-conducting sphere
at each point. Therefore, Gauss’s law in the
1. S correct
2. L
region r < R gives
∮
∮
E dA = E dA
3. X
4. Z
= E ( 4 π r 2) = q in
.
ɛ 0
Solving for E gives
5. G
E =
q in
4 π ɛ 0 r 2
6. Q
ρ 4
7. P
= 3 π r3
4 π ɛ 0 r 2
8. Y
= ρ r .
3 ɛ 0
9. M
Because ρ =
Q (by definition) and since
Explanation:
4
The electric field for R < r with
3 π R3
the sphere conducting and/or uniformly k = 1 , this expression for E can be written
as
non-conducting: In the region outside the 4 π ɛ 0
uniformly charged non-conducting sphere, we
have the same conditions as for the conducting
sphere when applying Gauss’s law, so
E =
Q r
4 π ɛ 0 R 3