Hypothesis Testing - Dependent Samples - SLC Home Page

CEGEP CHAMPLAIN - ST. LAWRENCE
201-510-LW: Business Statistics
Patrice Camiré
Hypothesis Testing - Dependent Samples
1. Ten government employees working for the ministry of revenue verifying personal income tax returns
were randomly chosen to attend a one-day conference on how to increase productivity. The following
table contains the average number of income tax returns verified per day for each of the ten employees
before and after attending the conference. (Assume that the table entries are normally distributed.)
Before After
9 10
11 11
12 11
13 14
10 10
12 11
8 9
9 11
15 14
9 9
(a) Test, at the 5% level of significance, the claim that an employee will be more productive after
attending the conference.
(b) Construct a 98% confidence interval for the true mean difference between an employee’s productivity
before and after attending the conference.
2. In a married couple, does the husband make more money than his wife To enquire about this, a
random sample of 8 married couples was taken. Here is the corresponding table of weekly wages:
(Assume weekly wages are normally distributed.)
Husband Wife
450 400
515 520
412 375
581 533
387 364
441 459
679 550
576 580
(a) Test, at the 3% level of significance, the claim that a husband makes more money than his wife.
(b) Construct a 90% confidence interval for the true mean difference between a husband’s salary and
his wife’s.
(c) Construct a 95% confidence interval for the true mean difference between a husband’s salary and
his wife’s.
(d) Are there any significant differences between the two confidence intervals Discuss.

3. A company created a new protein supplement in an attempt to increase the milk production of cows.
To test this new protein, 12 dairy cows were randomly selected for a before-after study. Here is the
corresponding table of daily milk production in liters: (Assume that a cow’s daily milk production is
normally distributed.)
Before After
21 21.7
20 23.1
22.4 23.7
22.4 23.5
20.5 21.9
19.2 22
20.7 22.5
22.3 24
22.1 22.5
19.4 20.3
20.9 22.8
21.8 21
(a) Test, at the 5% level of significance, the claim that dairy cows produce more milk when consuming
the new protein supplement.
(b) Construct a 99% confidence interval for the true mean difference between a cow’s milk production
before and after consuming the new protein supplement.
4. A financial company wants to determine whether or not a boss’ comments about the task an employee
must complete may be influential. To this end, the company designs the following experiment. They
randomly select 9 pairs of identical twins and have them complete a challenging two-hour test. The
pairs of twins are randomly split up into two groups. Group 1 is given the test with only indication
that they are allowed two hours. Group 2 is given the same instructions as Group 1, but is also told
that the test is very easy and they should only need about one hour. The following table shows the
test scores ouf of a hundred. (Assume that the scores are normally distributed.)
Twin 1 Twin 2
84 72
91 82
77 72
80 82
69 62
87 70
93 86
72 68
83 82
(a) Test, at the 1% level of significance, the claim that group 1 performed better than group 2.
(b) Construct a 95% confidence interval for the true mean difference between the scores of group 1
and group 2.

Answers
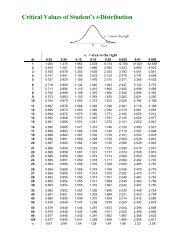
1. (a) d = after − before, H 0 : µ d = 0, H 1 : µ d > 0, α = 0.05, d = 0.2, s d ≈ 1.0328, t obs ≈ 0.612, df = 9,
R = [1.833, ∞)
We accept H 0 , so the evidence that the conference does increase productivity is not statistically
significant at the 5% level of significance.
(b) −0.72 ≤ µ d ≤ 1.12
2. (a) d = husband − wife, H 0 : µ d = 0, H 1 : µ d > 0, α = 0.03, d = 32.5, s d ≈ 46.687, t obs ≈ 1.969,
df = 7, R ≈ [2.365, ∞)
We accept H 0 , thus the evidence that a husband makes more money than his wife is not statistically
significant at the 3% level of significance.
(b) 1.22 ≤ µ d ≤ 63.78
(c) −6.54 ≤ µ d ≤ 71.54
(d) The key difference is that the first confidence interval contains strictly positive values whereas
the second confidence interval does contain negative values. What does this imply in terms of
possible conclusions
3. (a) d = after − before, H 0 : µ d = 0, H 1 : µ d > 0, α = 0.05, d ≈ 1.358, s d ≈ 1.0449, t obs ≈ 4.503,
df = 11, R = [1.796, ∞)
We reject H 0 , thus the evidence that cows produce more milk when consuming the new protein
supplement is statistically significant at the 5% level of significance.
(b) 0.42 ≤ µ d ≤ 2.30
4. (a) d = twin 2 − twin 1, H 0 : µ d = 0, H 1 : µ d < 0, α = 0.01, d ≈ −6.67, s d ≈ 5.679, t obs ≈ −3.522,
df = 8, R = (−∞, −2.896]
We reject H 0 , thus the evidence that group 1 performed better than group 2 is statistically
significant at the 1% level of significance.
(b) −11.03 ≤ µ d ≤ −2.30