Actor Critic Method: Maze Example - FIAS
Actor Critic Method: Maze Example - FIAS
Actor Critic Method: Maze Example - FIAS
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
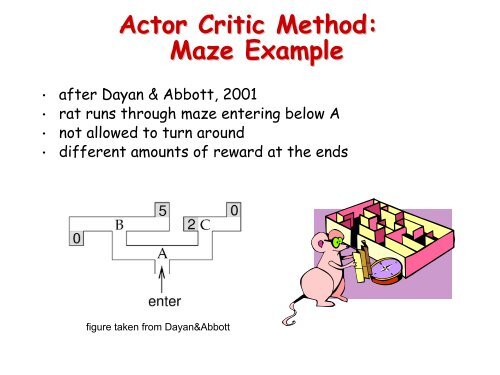
<strong>Actor</strong> <strong>Critic</strong> <strong>Method</strong>:<br />
<strong>Maze</strong> <strong>Example</strong><br />
• after Dayan & Abbott, 2001<br />
• rat runs through maze entering below A<br />
• not allowed to turn around<br />
• different amounts of reward at the ends<br />
figure taken from Dayan&Abbott
Solving the <strong>Maze</strong> Problem<br />
Assumptions:<br />
• state is fully observable (in contrast to only partially<br />
observable), i.e. the rat knows exactly where it is at any<br />
time<br />
• actions have deterministic consequences (in contrast to<br />
probabilistic)<br />
Idea: maintain and improve a stochastic policy which<br />
determines the action at each decision point (A,B,C)<br />
using action values and softmax decision rule<br />
<strong>Actor</strong> <strong>Critic</strong> Learning:<br />
• critic: use temporal difference learning to predict<br />
future rewards from A,B,C if current policy is followed<br />
• actor: maintain and improve the policy
<strong>Actor</strong>-<strong>Critic</strong> <strong>Method</strong><br />
Policy<br />
Agent<br />
<strong>Actor</strong><br />
state<br />
<strong>Critic</strong><br />
Value<br />
Function<br />
TD<br />
error<br />
action<br />
reward<br />
Environment
Formal Setup<br />
• state variable u (is rat at A,B, or C)<br />
• action value vector Q(u) describing policy (left/right)<br />
• softmax rule assigns probability of action a based on<br />
action values<br />
• immediate reward for taking action a in state u: r a (u)<br />
• expected future reward for starting in state u and<br />
following current policy: v(u) (state value function)<br />
• The rat estimates this with weights w(u)<br />
critic<br />
v<br />
actor<br />
Q L Q R<br />
figure taken from Dayan&Abbott<br />
w(A)<br />
A B C<br />
A B C
Policy Iteration<br />
• Two Observations:<br />
• We need to estimate the values of the states, but these depend<br />
on the rat’s current policy.<br />
• We need to chose better actions, but what action appears<br />
“better” depends on the values estimated above.<br />
• Idea (policy iteration): just iterate the two processes<br />
• Policy Evaluation (critic): estimate state value function (weights<br />
w(u)) using temporal difference learning.<br />
• Policy Improvement (actor): improve action values Q(u) based<br />
on estimated state values.
Policy Evaluation<br />
Initially, assume all action values are 0, i.e. left/right<br />
equally likely everywhere. What is the value of each state<br />
assuming there is no discounting<br />
True value of each state can be<br />
found by inspection:<br />
v(B) = ½(5+0)=2.5;<br />
v(C) = ½(2+0)=1;<br />
v(A) = ½(v(B)+v(C))=1.75.<br />
2.5 1<br />
1.75<br />
figure taken from Dayan&Abbott<br />
How can we learn these values through online experience
Temporal Difference Learning<br />
Idea: values of successive states are related. This is expressed<br />
through the Bellman equation:<br />
V<br />
π<br />
( s)<br />
{ s s}<br />
{ }<br />
π<br />
R s = s = E r + γV<br />
( s )<br />
= Eπ<br />
t<br />
π t 1<br />
t+<br />
t + 1 t<br />
=<br />
Deviations of estimated values of successive states from this<br />
relation need to be corrected. Define the temporal difference<br />
error as a (sampled) measure of such deviations:<br />
δ<br />
( t) r + V ( s ) 1<br />
−V<br />
( s )<br />
= γ<br />
t+ 1 t+<br />
t<br />
Now update the estimate of the value of the current state:<br />
V<br />
( s ) V ( s ) + ε[<br />
r + V ( s ) −V<br />
( s )]<br />
t<br />
← γ<br />
t t+ 1 t+<br />
1<br />
t
Policy Evaluation <strong>Example</strong><br />
w ( u)<br />
→ w(<br />
u) + εδ with є=0.5 and δ = ( u)<br />
+ v(<br />
u')<br />
− v(<br />
u)<br />
r a<br />
Thick lines are running average of weight values;<br />
figure taken from Dayan&Abbott
Note: Sutton and<br />
Barto book uses “p”<br />
for action<br />
preferences<br />
Q<br />
a'<br />
δ =<br />
r a<br />
Policy Improvement<br />
(using a so-called direct actor rule)<br />
( u)<br />
→ Qa'<br />
( u)<br />
+ ε ( δ<br />
aa'<br />
− p(<br />
a';<br />
u))<br />
δ<br />
( u)<br />
+ v(<br />
u')<br />
− v(<br />
u)<br />
positive if a’ was chosen, else negative<br />
, where<br />
positive if outcome better<br />
than expected, else negative<br />
p(a ’;u) is the softmax probability of choosing action a’ in<br />
state u as determined by Q a’ (u)<br />
This term is not strictly necessary but has the advantage<br />
that actions which are already chosen with very high<br />
probability only increase their Q value very slowly
Q<br />
a'<br />
δ =<br />
( u)<br />
→ Qa'<br />
( u)<br />
+ ε ( δ<br />
aa'<br />
− p(<br />
a';<br />
u))<br />
δ<br />
r a<br />
( u)<br />
+ v(<br />
u')<br />
− v(<br />
u)<br />
positive if a’ was chosen, else negative<br />
, where<br />
positive if outcome better<br />
than expected, else negative<br />
<strong>Example</strong>: consider starting out from random policy and assume<br />
state value estimates w(u) are accurate. Consider u=A:<br />
Rat will increase probability of<br />
going left in location A because:<br />
2.5 1<br />
1.75<br />
δ = 0 + v(<br />
B)<br />
− v(<br />
A)<br />
= 0.75<br />
δ = 0 + v(<br />
C)<br />
− v(<br />
A)<br />
= −0.75<br />
if left turn<br />
if right turn
Policy Improvement <strong>Example</strong><br />
•learning rate є=0.5<br />
• inverse temperature β=1<br />
figures taken from Dayan&Abbott