The Money Changing Problem Revisited - Universität Bielefeld

972 Sebastian Böcker and Zsuzsanna Lipták
6 Computational Results
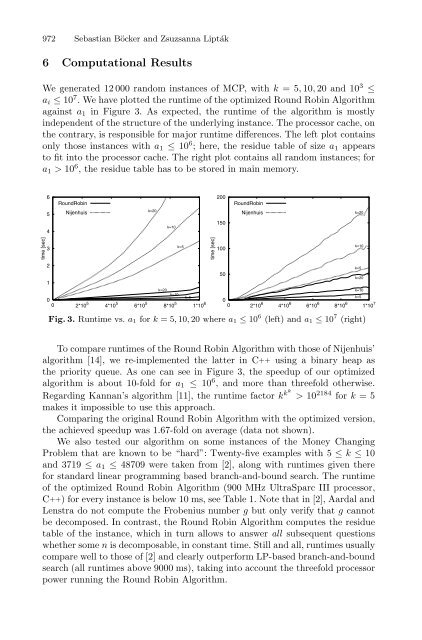
We generated 12 000 random instances of MCP, with k =5, 10, 20 and 10 3 ≤
a i ≤ 10 7 . We have plotted the runtime of the optimized Round Robin Algorithm
against a 1 in Figure 3. As expected, the runtime of the algorithm is mostly
independent of the structure of the underlying instance. The processor cache, on
the contrary, is responsible for major runtime differences. The left plot contains
only those instances with a 1 ≤ 10 6 ; here, the residue table of size a 1 appears
to fit into the processor cache. The right plot contains all random instances; for
a 1 > 10 6 , the residue table has to be stored in main memory.
6
RoundRobin
200
RoundRobin
5
Nijenhuis
k=20
Nijenhuis
k=20
4
k=10
150
time [sec]
k=5
3
time [sec]
k=10
100
2
k=5
50
k=20
1
k=20
k=10
k=10
k=5
k=5
0
0 2*10 5 4*10 5 6*10 5 8*10 5 1*10 6 0
0 2*10 6 4*10 6 6*10 6 8*10 6 1*10 7
Fig. 3. Runtime vs. a 1 for k =5, 10, 20 where a 1 ≤ 10 6 (left) and a 1 ≤ 10 7 (right)
To compare runtimes of the Round Robin Algorithm with those of Nijenhuis’
algorithm [14], we re-implemented the latter in C++ using a binary heap as
the priority queue. As one can see in Figure 3, the speedup of our optimized
algorithm is about 10-fold for a 1 ≤ 10 6 , and more than threefold otherwise.
Regarding Kannan’s algorithm [11], the runtime factor k kk > 10 2184 for k =5
makes it impossible to use this approach.
Comparing the original Round Robin Algorithm with the optimized version,
the achieved speedup was 1.67-fold on average (data not shown).
We also tested our algorithm on some instances of the Money Changing
Problem that are known to be “hard”: Twenty-five examples with 5 ≤ k ≤ 10
and 3719 ≤ a 1 ≤ 48709 were taken from [2], along with runtimes given there
for standard linear programming based branch-and-bound search. The runtime
of the optimized Round Robin Algorithm (900 MHz UltraSparc III processor,
C++) for every instance is below 10 ms, see Table 1. Note that in [2], Aardal and
Lenstra do not compute the Frobenius number g but only verify that g cannot
be decomposed. In contrast, the Round Robin Algorithm computes the residue
table of the instance, which in turn allows to answer all subsequent questions
whether some n is decomposable, in constant time. Still and all, runtimes usually
compare well to those of [2] and clearly outperform LP-based branch-and-bound
search (all runtimes above 9000 ms), taking into account the threefold processor
power running the Round Robin Algorithm.