Lecture Notes in Differential Equations - Bruce E. Shapiro

More documents

Recommendations

Info

$NAME: Math 103L: Exercise on Functions ... - Bruce E. Shapiro$

$Introducing Latex - Bruce E. Shapiro$

$Applied Differential Equations, Math 280 at CSUN - Bruce E. Shapiro$

$Math 103 Section 1.2: Linear Equations and ... - Bruce E. Shapiro$

34 LESSON 4. LINEAR EQUATIONS Figure 4.1: Different solutions for example 4.6. 2 1 0 1 2 2 1 0 1 2 The three solutions are illustrated in the figure 4.1. In cases (a) and (b), the domain of the solution that fits the initial condition excludes t = 0; but in case (c), the solution is continuous for all t. Furthermore, lim t→0 y is radically different in all three cases. With a little thought we see that ⎧ ⎪⎨ ∞, if y(1) > 2/3 lim y(t) = 0, if y(1) = 2/3 t→0 + ⎪ ⎩ −∞, if y(1) < 2/3 (4.80) As t → ∞ all of the solutions become asymptotic to the curve y = 2t 2 /3. The side on of the curved asymptote on which the initial conditions falls determines the behavior of the solution for small t. What if we were given the initial condition y(0) = 0 in the previous example? Clearly the solution y = 2t 2 /3 satisfies this condition, but if we try to plug the initial condition into the general solution y = 2t2 3 + C t 4 (4.81) we have a problem because of the C/t 4 term. One possible approach is to multiply through by the offending t 4 factor: yt 4 = 2 3 t6 + C (4.82)
35 Substituting y = t = 0 in this immediately yields C = 0. This problem is a direct consequence of the fact that we divided our equation through by t 4 previously to get an express solution for y(t) (see the transition from equation 4.72 to equation 4.73): this division is only allowed when t ≠ 0. Example 4.7. Solve the initial value problem dy dt − 2ty = √ 2 ⎫ ⎬ π ⎭ y(0) = 0 (4.83) Since p(t) = −2t, an integrating factor is (∫ ) µ = exp −2tdt = e −t2 (4.84) Following our usual procedure we get d ( ye −t2) = √ 2 e −t2 (4.85) dt π If we try to solve the indefinite integral we end up with ye −t2 = √ 2 ∫ e −t2 dt + C (4.86) π Unfortunately, there is no exact solution for the indefinite integral on the right. Instead we introduce a new concept, of finding a definite integral. We will use as our lower limit of integration the initial conditions, which means t = 0; and as our upper limit of integration, some unknown variable u. Then ∫ u Then we have 0 d ( ye −t2) dt = dt ∫ u ( ye −t2) ( − ye −t2) = 2 ∫ u √ t=0 t=u π 0 2 √ π e −t2 dt (4.87) Using the initial condition y(0) = 0, the left hand side becomes 0 e −t2 dt (4.88) y(u)e −(u)2 − y(0)e −(0)2 = ye −u2 (4.89) hence ye −u2 = √ 2 ∫ u e −t2 dt (4.90) π 0
Page 1 and 2: Lecture Notes in Differential Equat
Page 3 and 4: Contents Front Cover . . . . . . .
Page 5 and 6: CONTENTS v Dedicated to the hundred
Page 7 and 8: Preface These lecture notes on diff
Page 9 and 10: Lesson 1 Basic Concepts A different
Page 11 and 12: 3 Definition 1.2 (Solution, ODE). A
Page 13 and 14: 5 1.22 is restricted to being a pos
Page 15 and 16: 7 Figure 1.1 illustrates what this
Page 17 and 18: 9 We will study linear equations in
Page 19 and 20: Lesson 2 A Geometric View One way t
Page 21 and 22: 13 We can extend this geometric int
Page 23 and 24: 15 that since the slope of the solu
Page 25 and 26: Lesson 3 Separable Equations An ODE
Page 27 and 28: 19 Since it is not possible to solv
Page 29 and 30: 21 where M(t) = −a(t) and N(y) =
Page 31 and 32: 23 Example 3.10. Find a general sol
Page 33 and 34: Lesson 4 Linear Equations Recall th
Page 35 and 36: 27 So far any function µ will work
Page 37 and 38: 29 Example 4.1. Solve the different
Page 39 and 40: 31 Since p(t) = 1 (the coefficient
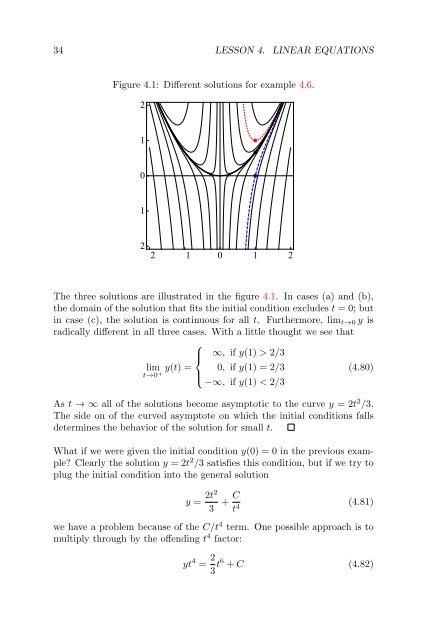
Page 41: 33 Multiplying equation 4.68 by µ
Page 45 and 46: 37 ∫ t t 0 Evaluating the integra
Page 47 and 48: Lesson 5 Bernoulli Equations The Be
Page 49 and 50: 41 This is a Bernoulli equation wit
Page 51 and 52: Lesson 6 Exponential Relaxation One
Page 53 and 54: 45 Exponential Runaway First we con
Page 55 and 56: 47 Figure 6.2: Illustration of the
Page 57 and 58: 49 This is identical to with Theref
Page 59 and 60: 51 this becomes a first-order ODE i
Page 61 and 62: Lesson 7 Autonomous Differential Eq
Page 63 and 64: 55 Figure 7.1: A plot of the right-
Page 65 and 66: 57 Figure 7.2: Solutions of the log
Page 67 and 68: 59 Figure 7.4: Solutions of the thr
Page 69 and 70: Lesson 8 Homogeneous Equations Defi
Page 71 and 72: 63 where z = y/t, the differential
Page 73 and 74: Lesson 9 Exact Equations We can re-
Page 75 and 76: 67 Now compare equation (9.2) with
Page 77 and 78: 69 Hence dg dy = 0 =⇒ g = C′ (9
Page 79 and 80: 71 From the first of equations (9.5
Page 81 and 82: 73 Differentiating equations (9.81)
Page 83 and 84: 75 This has the form Mdt + Ndy = 0
Page 85 and 86: Lesson 10 Integrating Factors Defin
Page 87 and 88: 79 Differentiating with respect to
Page 89 and 90: 81 Proof. In each of the five cases
Page 91 and 92: 83 as required by equation (10.31).
Page 93 and 94:
85 Since M y ≠ N t , equation (10
Page 95 and 96:
87 the revised equation (10.100) is
Page 97 and 98:
89 Substituting (10.129) into (10.1
Page 99 and 100:
Lesson 11 Method of Successive Appr
Page 101 and 102:
93 because the integral is zero (th
Page 103 and 104:
95 Example 11.1. Construct the Pica
Page 105 and 106:
97 We can then plug this expression
Page 107 and 108:
Lesson 12 Existence of Solutions* I
Page 109 and 110:
101 • Interchangeability of Limit
Page 111 and 112:
103 But on the square −1 ≤ t
Page 113 and 114:
105 Thus lim φ n = φ 0 + lim n→
Page 115 and 116:
107 because the right hand side doe
Page 117 and 118:
Lesson 13 Uniqueness of Solutions*
Page 119 and 120:
111 The proof of theorem (13.1) is
Page 121 and 122:
113 But δ(t) is an absolute value,
Page 123 and 124:
115 Substituting (13.66) into (13.6
Page 125 and 126:
Lesson 14 Review of Linear Algebra
Page 127 and 128:
119 Definition 14.10. An m × n (or
Page 129 and 130:
121 Definition 14.19. Matrix Multip
Page 131 and 132:
123 In practical terms, computation
Page 133 and 134:
125 Simplifying 4x − 2 + 3z = 0 (
Page 135 and 136:
Lesson 15 Linear Operators and Vect
Page 137 and 138:
129 Example 15.3. By a similar argu
Page 139 and 140:
131 Therefore ‖y + z‖ 2 ≤ ‖
Page 141 and 142:
133 Definition 15.5. Two vectors y,
Page 143 and 144:
Lesson 16 Linear Equations With Con
Page 145 and 146:
137 Hence both r = 1 and r = 3. Thi
Page 147 and 148:
139 The second order linear initial
Page 149 and 150:
141 The general solution to is give
Page 151 and 152:
Lesson 17 Some Special Substitution
Page 153 and 154:
145 Therefore since z = y ′ , Int
Page 155 and 156:
147 Example 17.5. Solve yy ′′ +
Page 157 and 158:
149 where I is the identity matrix.
Page 159 and 160:
151 can be rewritten by solving a =
Page 161 and 162:
Lesson 18 Complex Roots We know for
Page 163 and 164:
155 Theorem 18.2. Euler’s Formula
Page 165 and 166:
157 For k = 0, 1, 2, . . . , n −
Page 167 and 168:
159 and its roots are given by The
Page 169 and 170:
161 The motivation for equation 18.
Page 171 and 172:
Lesson 19 Method of Undetermined Co
Page 173 and 174:
165 3. If f(t) = e rt and r is a ro
Page 175 and 176:
167 Example 19.4. Solve ⎫ y ′
Page 177 and 178:
169 Adding the two equations gives
Page 179 and 180:
Lesson 20 The Wronskian We have see
Page 181 and 182:
173 Definition 20.1. The Wronskian
Page 183 and 184:
175 Example 20.3. Show that y = sin
Page 185 and 186:
177 and therefore the system of equ
Page 187 and 188:
Lesson 21 Reduction of Order The me
Page 189 and 190:
181 The method of reduction of orde
Page 191 and 192:
183 Plugging these into Bessel’s
Page 193 and 194:
185 Example 21.5. Find a second sol
Page 195 and 196:
Lesson 22 Non-homogeneous Equations
Page 197 and 198:
189 where r 1 and r 2 are the roots
Page 199 and 200:
191 This is a first order linear eq
Page 201 and 202:
193 Theorem 22.5. Properties of the
Page 203 and 204:
195 where (∫ ν(t) = exp ) −r 2
Page 205 and 206:
197 The characteristic equation is
Page 207 and 208:
Lesson 23 Method of Annihilators In
Page 209 and 210:
201 Theorem 23.5. (D 2 − 2aD + (a
Page 211 and 212:
203 The method of annihilators is r
Page 213 and 214:
Lesson 24 Variation of Parameters T
Page 215 and 216:
207 Substituting into equation (24.
Page 217 and 218:
209 Example 24.3. Solve the initial
Page 219 and 220:
Lesson 25 Harmonic Oscillations If
Page 221 and 222:
213 It is standard to define a new
Page 223 and 224:
215 As with the unforced case, we c
Page 225 and 226:
Lesson 26 General Existence Theory*
Page 227 and 228:
219 In the case just proven, there
Page 229 and 230:
221 Theorem 26.5. Under the same co
Page 231 and 232:
223 Since K n /(1 − K) → 0 as n
Page 233 and 234:
225 for any φ ∈ V. Let g, h be f
Page 235 and 236:
Lesson 27 Higher Order Linear Equat
Page 237 and 238:
229 L n+1 (e rt y) = e rt a n (D +
Page 239 and 240:
231 Example 27.2. Find the general
Page 241 and 242:
233 Differentiating, u ′ (t) = d
Page 243 and 244:
235 Integrating, − 2K |t − t 0
Page 245 and 246:
237 a closed form expression for a
Page 247 and 248:
Page 249 and 250:
241 The characteristic equation is
Page 251 and 252:
243 The Wronskian In this section w
Page 253 and 254:
245 Certainly every φ(t) given by
Page 255 and 256:
247 the differential equation. Over
Page 257 and 258:
249 By the lemma, to obtain the der
Page 259 and 260:
Page 261 and 262:
253 So that f(t) = a n (t)y[ (n) +
Page 263 and 264:
Lesson 28 Series Solutions In many
Page 265 and 266:
257 Changing the index of the secon
Page 267 and 268:
259 Since the first two terms (corr
Page 269 and 270:
261 Hence ∞∑ ∞∑ ∞∑ 0 =
Page 271 and 272:
263 has an analytic solution at t =
Page 273 and 274:
265 By the triangle inequality, |(k
Page 275 and 276:
267 Table 28.1: Table of Special Fu
Page 277 and 278:
269 Thus y = a 0 ( 1 + 1 6 t3 + 1 +
Page 279 and 280:
271 into (28.114) and collect terms
Page 281 and 282:
273 Summary of Power series method.
Page 283 and 284:
Lesson 29 Regular Singularities The
Page 285 and 286:
277 ∑ ∞ ∞∑ ∞∑ 0 = t 2 a
Page 287 and 288:
279 Case 2: Two equal real roots. S
Page 289 and 290:
281 Example 29.6. Solve t 2 y ′
Page 291 and 292:
Lesson 30 The Method of Frobenius I
Page 293 and 294:
285 This is a homogeneous linear eq
Page 295 and 296:
287 Example 30.4. Find a Frobenius
Page 297 and 298:
289 Thus a Frobenius solution is y
Page 299 and 300:
291 Example 30.6. Find the form of
Page 301 and 302:
293 term by term to (30.97). Starti
Page 303 and 304:
295 Let j = n − k. Then |n − 1
Page 305 and 306:
297 is a solution of (t − t 0 ) 2
Page 307 and 308:
299 Evaluation of the integral depe
Page 309 and 310:
301 Example 30.8. In example 30.4 w
Page 311 and 312:
Lesson 31 Linear Systems The genera
Page 313 and 314:
305 is where λ 2 − T λ + ∆ =
Page 315 and 316:
307 (b) If λ 1 ≠ λ 2 ∈ R, i.e
Page 317 and 318:
309 We will verify (31.54) by induc
Page 319 and 320:
311 The Jordan Form Let A be a squa
Page 321 and 322:
313 y = 1 [( ) ( ) ] ( ) 4 1 e 2t 1
Page 323 and 324:
315 Theorem 31.8. (Abel’s Formula
Page 325 and 326:
317 By a similar argument, the seco
Page 327 and 328:
319 we can replace (31.118) with a
Page 329 and 330:
321 Corollary 31.12. The generalize
Page 331 and 332:
323 where (A − λI)w 2 = w 1 , i.
Page 333 and 334:
325 so that λ = 3, −5. The eigen
Page 335 and 336:
327 Non-constant Coefficients We ca
Page 337 and 338:
329 we find that ∫ M(t)g(t)dt = (
Page 339 and 340:
Lesson 32 The Laplace Transform Bas
Page 341 and 342:
333 Figure 32.1: A piecewise contin
Page 343 and 344:
335 Example 32.4. From integral A.1
Page 345 and 346:
337 apply this result iteratively.
Page 347 and 348:
L [ t x−1] [ ] 1 d = L x dt tx =
Page 349 and 350:
341 Equating numerators and expandi
Page 351 and 352:
343 Derivatives of the Laplace Tran
Page 353 and 354:
345 can be written as as illustrate
Page 355 and 356:
347 Translations in the Laplace Var
Page 357 and 358:
349 Summary of Translation Formulas
Page 359 and 360:
351 The inverse transform is [ ] f(
Page 361 and 362:
353 Example 32.18. Find the Laplace
Page 363 and 364:
355 Similarly, we can express a uni
Page 365 and 366:
357 Figure 32.7: Solution of exampl
Page 367 and 368:
Lesson 33 Numerical Methods Euler
Page 369 and 370:
361 Figure 33.1: Illustration of Eu
Page 371 and 372:
363 y 4 = y 3 + hf(t 3 , y 3 ) (33.
Page 373 and 374:
365 Figure 33.3: Illustration of th
Page 375 and 376:
367 result with a smaller step size
Page 377 and 378:
369 Expanding the final term in a T
Page 379 and 380:
371 k 2 = y 0 + h 2 f(t 0, k 1 ) (3
Page 381 and 382:
Lesson 34 Critical Points of Autono
Page 383 and 384:
375 Since both f and g are differen
Page 385 and 386:
377 Using the cos π/4 = √ 2/2 an
Page 387 and 388:
379 values, of the matrix. We find
Page 389 and 390:
381 Distinct Real Nonzero Eigenvalu
Page 391 and 392:
383 eigendirection {λ 1 , v 1 }dom
Page 393 and 394:
385 Figure 34.5: Phase portraits ty
Page 395 and 396:
387 Complex Conjugate Pair with non
Page 397 and 398:
389 The angular change is described
Page 399 and 400:
391 Figure 34.8: Topological instab
Page 401 and 402:
393 Figure 34.10: phase portraits f
Page 403 and 404:
Appendix A Table of Integrals Basic
Page 405 and 406:
397 ∫ x √ x − adx = 2 3 a(x
Page 407 and 408:
399 ∫ x √ ax2 + bx + c dx = 1 a
Page 409 and 410:
401 ∫ ∫ ∫ ∫ e ax2 dx = −
Page 411 and 412:
403 ∫ tan 3 axdx = 1 a ln cos ax
Page 413 and 414:
405 Products of Trigonometric Funct
Page 415 and 416:
Appendix B Table of Laplace Transfo
Page 417 and 418:
409 e at cosh kt t sin kt t cos kt
Page 419 and 420:
Appendix C Summary of Methods First
Page 421 and 422:
413 The resulting equation is linea
Page 423 and 424:
415 for y once z is known. Method o
Page 425 and 426:
Bibliography [1] Bear, H.S. Differe
Page 427 and 428:
BIBLIOGRAPHY 419
Page 429 and 430:
BIBLIOGRAPHY 421
show all

Lecture Notes in Differential Equations - Bruce E. Shapiro

Create successful ePaper yourself

Delete template?

Save as template?