Abstracts - KTH Mechanics

7
Stability of pulsatile flow through a pipe
Linganagari Abhijeeth Reddy ∗ ,Kirti Chandra Sahu † , Rama Govindarajan †
Pulsatile flow through a pipe has been a topic of interest 1 because of its relevance
to the blood flow through arteries. (Arterial flow is of course very complicated but
we confine ourselves here to the effect of the pulsatile nature of the flow.) Stability
of pulsatile flow in a plane channel has been studed by Straatman et al. using a
Floquet analysis. They find that pulsatile flow is always destabilising 2 . In a recent
paper 3 Fedele et al. have studied the stability of pulsatile pipe flow for axisymmetric
disturbances. Although all eigen modes are decaying, a small transient growth of the
disturbances was found for a short time. In this work, we depart in two ways from the
study of Fedele et al. (1) the flow is taken to be periodic but not sinusoidal, which is
closer to arterial flow, (2) we consider non-axisymmetric disturbances which are often
more unstable. Prescribing periodic velocity profiles at the inlet, we solve the Navier-
Stokes equation directly using a full-multigrid algorithm on a parallel machine 4 to get
the basic flow. A Floquet stability analysis is then conducted. A sample basic flow
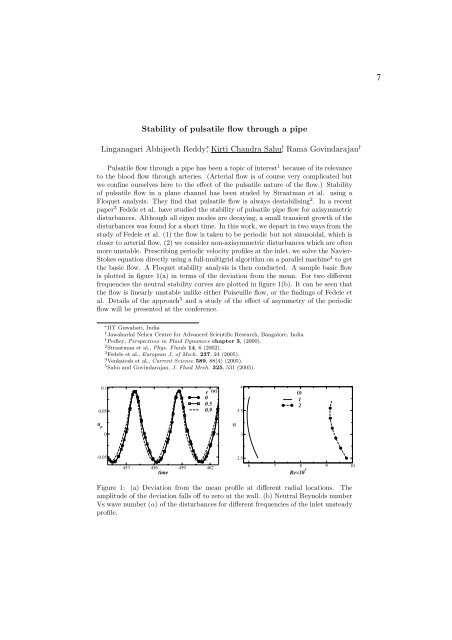
is plotted in figure 1(a) in terms of the deviation from the mean. For two different
frequencies the neutral stability curves are plotted in figure 1(b). It can be seen that
the flow is linearly unstable unlike either Poiseuille flow, or the findings of Fedele et
al. Details of the approach 5 andastudyoftheeffectofasymmetryoftheperiodic
flow will be presented at the conference.
∗ IIT Guwahati, India
† Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, India
1 Pedley, Perspectives in Fluid Dynamics chapter 3, (2000).
2 Straatman et al., Phys. Fluids 14, 6 (2002).
3 Fedele et al., European J. of Mech. 237, 24 (2005).
4 Venkatesh et al., Current Science 589, 88(4) (2005).
5 Sahu and Govindarajan, J. Fluid Mech. 325, 531 (2005).
0.1
0
0.5
0.05
0.9
u p
0
α
4
3.5
3
ω
1
2
r (a) 6 7 8 9 10
-0.05
453 456 459 462
time
2.5
Re×10 3
Figure 1: (a) Deviation from the mean profile at different radial locations. The
amplitude of the deviation falls off to zero at the wall. (b) Neutral Reynolds number
Vs wavenumber(α) of the disturbances for different frequencies of the inlet unsteady
profile.