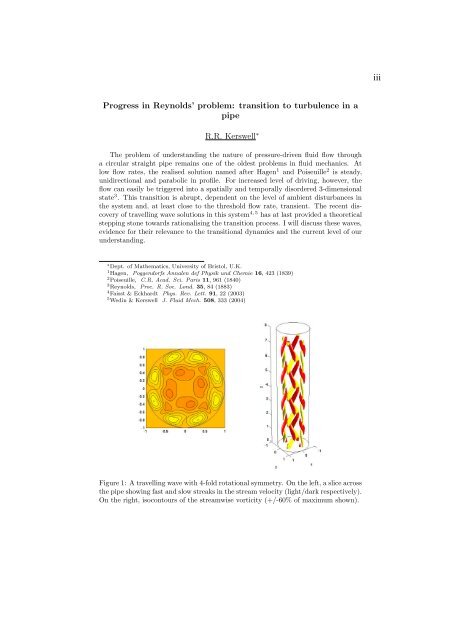
- Page 1: EFMC6 KTH Electronic version Abstra
- Page 5: Euromech Fluid Mechanics Lecturer H
- Page 10 and 11: iv Slip Behavior at Liquid/Solid In
- Page 12 and 13: I K M O Q S I U I K W X Y W [ \ \ ^
- Page 14 and 15: viii Premixed Turbulent combustion
- Page 17: Session 1
- Page 20 and 21: 2 Global stability of jets and sens
- Page 22 and 23: 4 Control of instabilities in a cav
- Page 24 and 25: 6 The dispersal, decay and instabil
- Page 26 and 27: 8 Steady and pulsatile flow through
- Page 28: 10 Pulsatile flows in pipes with fi
- Page 31 and 32: 13 Global stability of the rotating
- Page 33 and 34: 15 Continuous Spectrum Growth and M
- Page 35 and 36: 17 The influence of centrifugal buo
- Page 37 and 38: 19 Prediction of wall bounded flows
- Page 39 and 40: 21 Uncertainty Quantification in La
- Page 41 and 42: 23 Stratified turbulence G. Brethou
- Page 43 and 44: 25 Investigations of turbulence sta
- Page 45 and 46: 27 Coupling weather-scale flow with
- Page 47 and 48: 29 Flow Separation from a Free Surf
- Page 49 and 50: 31 Phase-Field Simulations of Free
- Page 51 and 52: 33 Evaluation of a universal transi
- Page 53 and 54: 35 Computations of turbulent bounda
- Page 55 and 56: 37 Flow Developments in Smooth Wall
- Page 57 and 58: 39 Super-late stages of boundary-la
- Page 59 and 60:
41 Low-speed streaks developing at
- Page 61:
43 Direct Numerical Simulation of L
- Page 64 and 65:
44 Axisymmetric absolute instabilit
- Page 66:
46
- Page 69 and 70:
49 Application of the ray-tracing t
- Page 71 and 72:
51 Leaky Waves in Supersonic Bounda
- Page 73 and 74:
53 Solving turbulent wall flow in 2
- Page 75 and 76:
55 Development of a 3D transient in
- Page 78 and 79:
58 Upper bounds for the long-time a
- Page 80 and 81:
60 Numerical Simulations of Rigid F
- Page 82 and 83:
62 On the translational and rotatio
- Page 84 and 85:
64 A Shell-Model Study of Turbulent
- Page 86 and 87:
v 66 Using CSP for Modeling Burgers
- Page 88 and 89:
68 High Spatially Resolved Velocity
- Page 91:
71 Dynamic Lift of Airfoils R. Grü
- Page 94 and 95:
72 Experimental study on the bounda
- Page 96 and 97:
74 Natural sinuous and varicose bre
- Page 99 and 100:
77 Numerical simulation of the thre
- Page 101 and 102:
79 Effects of the flexibility of th
- Page 103 and 104:
81 Wave forerunners of longitudinal
- Page 105 and 106:
83 Stability and sensitivity analys
- Page 107 and 108:
85 Stability of reacting gas jets J
- Page 109 and 110:
87 Elastocapillarity in wet hairs J
- Page 111 and 112:
89 Open Capillary Channel Flows (CC
- Page 113:
91 Stick-slip motion of droplets of
- Page 116 and 117:
94 A general theory for stratified
- Page 118 and 119:
£ ¥ § © £ ¥ © ¡
- Page 120 and 121:
98 The influence of the density max
- Page 122 and 123:
100 TRANSIENT DISPLACEMENT OF A NEW
- Page 124 and 125:
102 Experimental study of the effec
- Page 126 and 127:
104 Numerical modeling of heat tran
- Page 128 and 129:
106 Turbulent thermal convection ov
- Page 130 and 131:
108
- Page 132 and 133:
110 Modelling of optimal vortex rin
- Page 134 and 135:
112 The effect of a sphere on a swi
- Page 136 and 137:
114 Three-dimensional stability of
- Page 139 and 140:
Session 4
- Page 141 and 142:
117
- Page 143 and 144:
119 Nonlinear long waves on an inte
- Page 145 and 146:
121 Three-dimensional gravity-capil
- Page 147 and 148:
123 Linear and non-linear theory of
- Page 149 and 150:
125 Surface oscillations of liquid
- Page 151 and 152:
127 Waves above turbulence R. Savel
- Page 153 and 154:
129
- Page 155 and 156:
131 Investigation of flow structure
- Page 157 and 158:
133 Simultaneous density and concen
- Page 159:
135 Introduction of newly developed
- Page 162 and 163:
136 A Simple Model for Gas-Grain Tw
- Page 164 and 165:
138 Dynamics of heavy particles nea
- Page 166 and 167:
140 Stability of dusty gas flow in
- Page 168 and 169:
142 Joint fluid-particle pdf modeli
- Page 170 and 171:
144 Three-dimensional stability of
- Page 172 and 173:
146 Mixing by merging Kelvin-Helmho
- Page 174 and 175:
148
- Page 176 and 177:
150 a Institute of Thermophysics, 6
- Page 178 and 179:
152 Direct numerical simulations of
- Page 180 and 181:
154 Study of anisotropy in purely s
- Page 182 and 183:
156 Direct numerical simulation of
- Page 184 and 185:
159 Assessment of a wavelet based c
- Page 186 and 187:
157 Numerical study of turbulence i
- Page 188 and 189:
162
- Page 190 and 191:
164 Flowcontrol with crosswise grov
- Page 192 and 193:
166 Experiments on the reverse Bén
- Page 194 and 195:
168 Kinematic-dynamic correspondenc
- Page 196 and 197:
170 Three-dimensional structures in
- Page 198 and 199:
172 Lagrangian (physical) analysis
- Page 201 and 202:
173 The evolution of energy in flow
- Page 203 and 204:
175
- Page 205 and 206:
177 Mechanisms of gas migration thr
- Page 207 and 208:
179 Surface waves in coupled channe
- Page 209 and 210:
181 Validation of urban dispersion
- Page 211 and 212:
183 Numerical study of flow pattern
- Page 213 and 214:
185 Generation of metal nanodroplet
- Page 215 and 216:
187 Oscillations of Thin Liquid She
- Page 217 and 218:
189 3D chaotic mixing inside drops
- Page 219 and 220:
191 The interaction between negativ
- Page 221 and 222:
193 Coherent Large-Scale Structures
- Page 223 and 224:
195 Turbulent mixing in the entry r
- Page 225 and 226:
197 0.16 0.16 1.4 0.14 0.14 1.3 1.2
- Page 227 and 228:
199 Experiments on vortex pair dyna
- Page 229:
List of authors Ordinary lectures a
- Page 232 and 233:
LIST OF AUTHORS Borel H. 340 Castro
- Page 234 and 235:
LIST OF AUTHORS Glezer A. 259 Haspa
- Page 236 and 237:
LIST OF AUTHORS Lebon L. 238, 266 M
- Page 238 and 239:
LIST OF AUTHORS Poplavskaya T. V. 4
- Page 240:
LIST OF AUTHORS Tuzi R. 11 Wolters