Test 3 - Faculty.lasierra.edu

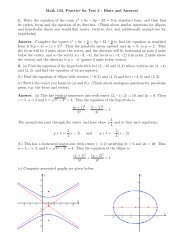
(Critical Region) For α = .01 on a right-tailed test, the critical region is z ≥ 2.33, because thez = 2.86 > 2.33 is in the critical region, as with the P -value, we reject H 0 , the evidence suggeststhat on average SDA’s live longer than 76 years.III.F.4. The 13 Feb 2007 AAA survey of gasoline prices found that the average price for regular gasin Riverside was 2.602 (from AAA website). Suppose the Riverside Chamber of Commerce thoughtthis price was not accurate, and wanted to prove that the gas price is actually lower. Suppose theirsurvey of 80 randomly selected gas stations in Riverside and had a sample mean ¯x = 2.576 with astandard deviation of 0.152 which we assume is also the population standard deviation. Conduct anhypothesis test to determine if the mean is lower than 2.602 using a 5% level of significance.Answer. The hypotheses are: H 0 : µ = 2.602 and H 1 : µ < 2.602, and α = .05.z =2.576 − 2.602.152/ √ 80≈ −1.53The P-value is P (z < −1.53) = .0618. Because the P-value is larger than α, there is not sufficientevidence at the 5% significance level to show that the mean gas price in Riverside is less than 2.602.III.F.5. (a) Find the critical region if a two-tailed test on a mean is conducted using a large sampleat a level of significance of .01.(b) Explain what type I and type II errors are in hypothesis tests.(c) What is the probability with which we are willing to risk a type I error called?Answer. (a) With the help of the normal table in the front cover, we find that the critical regionis z ≤ −2.58 or z ≥ 2.58.(b) See text Section 9.1.(c) The level of significance, which is denoted by α.III.F.6. (a) A developer wishes to test whether the mean depth of water below the surface in alarge development tract was less than 500 feet. The sample data was as follows: n = 32 test holes,the sample mean was 486 feet, and the standard deviation was 53 feet, assume that this is thepopulation standard deviation σ = 53. Complete the test by computing the Pvalue, and report theconclusion for a 1% level of significance.(b) What would the conclusion of the test be for a level of significance of α = .05.(c) What type of error was possibly made in (b)?Answer. H 0 : µ = 500H 1 : µ < 500Using the sample data, we computez =486 − 50053 √32= −1.49Thus the Pvalue is P (z < −1.49) = .0681 We would not reject the null hypothesis at a level ofsignificance of .01, because the P-value is larger than 0.01. Thus the data does not show at the 5%significance level that the average water depth is less than 500 feet.