A Random Number Generator Test Suite for the C++ ... - ETH Zürich

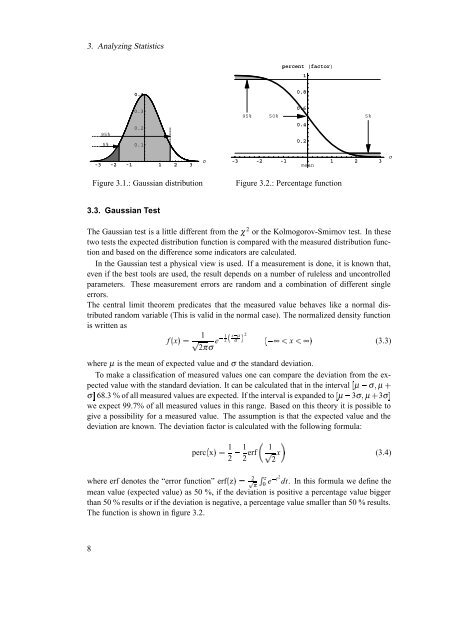
3. Analyzing Statisticspercent factor10.40.895%5%0.30.20.195%0.650% 5%0.40.2-3 -2 -1 1 2 3Σ-3 -2 -1 1 2 3meanΣFigure 3.1.: Gaussian distributionFigure 3.2.: Percentage function3.3. Gaussian TestThe Gaussian test is a little different from the χ 2 or the Kolmogorov-Smirnov test. In thesetwo tests the expected distribution function is compared with the measured distribution functionand based on the difference some indicators are calculated.In the Gaussian test a physical view is used. If a measurement is done, it is known that,even if the best tools are used, the result depends on a number of ruleless and uncontrolledparameters. These measurement errors are random and a combination of different singleerrors.The central limit theorem predicates that the measured value behaves like a normal distributedrandom variable (This is valid in the normal case). The normalized density functionis written as1 1 µ2§xσ¨2 2πσ§ e£ ¢¥ f§x¨¡ x ¡ ∞¨ (3.3)∞where µ is the mean of expected value and σ the standard deviation.To make a classification of measured values one can compare the deviation from the expectedvalue with the standard deviation. It can be calculated that in the interval σ µ¤ µ ¢68.3 % of all measured values are expected. If the interval is expanded to 3σ µ µ¤ 3σ£σ£we expect 99.7% of all measured values in this range. Based on this theory it is possible togive a possibility for a measured value. The assumption is that the expected value and thedeviation are known. The deviation factor is calculated with the following ¢ formula:1 1 1erf perc§x¨2where erf denotes the¥2“error ¤ function”2z t 2π 0 dt. In this formula we define themean value (expected value) as 50 %, if the deviation is positive a percentage value biggererf§z¨¥than 50 % results or if the deviation is negative, a percentage value smaller than 50 % results.The function is shown in e£ figure 3.2.¥(3.4)¢ 2x8