Exercises for Section 12.4

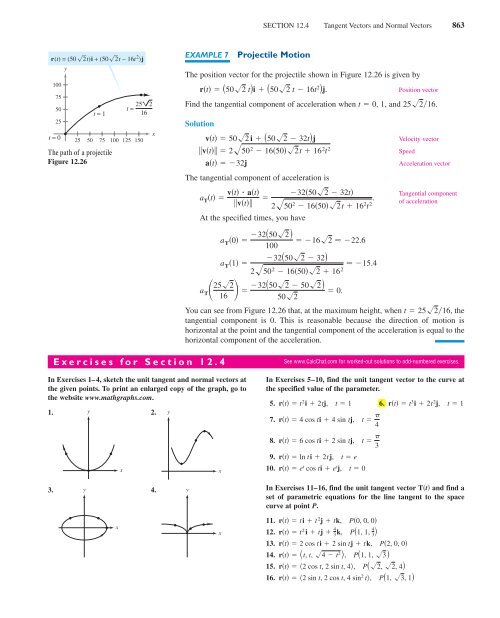
332460_1204.qxd 11/5/04 9:07 AM Page 863SECTION 12.4 Tangent Vectors and Normal Vectors 863r(t) = (50 2t)i + (50 2t − 16t 2 )j100755025t = 0yt = 125 50 75The path of a projectileFigure 12.2625 2t =16100 125 150xEXAMPLE 7Projectile MotionThe position vector for the projectile shown in Figure 12.26 is given byrt 502 ti 502 t 16t 2 j.Position vectorFind the tangential component of acceleration when t 0, 1, and 25216.Solutionvt 502 i 502 32tjvt 250 2 16502t 16 2 t 2at 32jThe tangential component of acceleration isa T t vt atvtAt the specified times, you have32502 32t250 2 16502t 16 2 t 2 .a T 0 32502 162 22.610032502 32a T 1 15.4250 2 16502 16 2a T 252 32502 50216 0.502Velocity vectorSpeedAcceleration vectorTangential componentof accelerationYou can see from Figure 12.26 that, at the maximum height, when t 25216, thetangential component is 0. This is reasonable because the direction of motion ishorizontal at the point and the tangential component of the acceleration is equal to thehorizontal component of the acceleration.Exercises for Section 12.4In Exercises 1–4, sketch the unit tangent and normal vectors atthe given points. To print an enlarged copy of the graph, go tothe website www.mathgraphs.com.1. y2.xyxSee www.CalcChat.com for worked-out solutions to odd-numbered exercises.In Exercises 5–10, find the unit tangent vector to the curve atthe specified value of the parameter.5. rt t 2 i 2tj, t 1 6. rt t 3 i 2t 2 j, t 17. rt 4 cos ti 4 sin tj, t 48. rt 6 cos ti 2 sin tj, t 39. rt ln ti 2tj, t e10. rt e t cos ti e t j, t 03. y4.xyxIn Exercises 11–16, find the unit tangent vector Tt and find aset of parametric equations for the line tangent to the spacecurve at point P.11. rt ti t 2 j tk, P0, 0, 012. rt t 2 i t j 4 3 k, P1, 1, 4 313. rt 2 cos ti 2 sin tj tk, P2, 0, 014. rt t, t, 4 t 2 , P1, 1, 3 15. rt 2 cos t, 2 sin t, 4, P2, 2, 416. rt 2 sin t, 2 cos t, 4 sin 2 t, P1, 3, 1

332460_1204.qxd 11/5/04 9:07 AM Page 864864 CHAPTER 12 Vector-Valued FunctionsIn Exercises 17 and 18, use a computer algebra system to graphthe space curve. Then find Tt and find a set of parametricequations for the line tangent to the space curve at point P.Graph the tangent line.17. rt t, t 2 , 2t 3 3, P3, 9, 1818. rt 3 cos ti 4 sin tj 1 2 tk,Linear Approximation In Exercises 19 and 20, find a set ofparametric equations for the tangent line to the graph at t t 0and use the equations for the line to approximate rt 0 0.1.22. rt t, cos t, sin t,In Exercises 23–30, find the principal unit normal vector to thecurve at the specified value of the parameter.23.24.25.26. rt 3 cos ti 3 sin t j,29.30.us 1 4 s, 2s, 3 s,rt ti 1 2 t2 j, t 2rt ti 6 t j, t 3rt ln ti t 1j,s 8t 0t 227. rt ti t 2 j ln tk, t 128. rt 2ti e t j e t k, t 0rt 6 cos ti 6 sin tj k, t 34rt cos ti 2 sin tj k, t 4In Exercises 31–34, find vt, at, Tt, and Nt (if it exists) foran object moving along the path given by the vector-valuedfunction rt. Use the results to determine the form of the path.Is the speed of the object constant or changing?31. rt 4ti32. rt 4ti 2tj33. rt 4t 2 i34. rt t 2 j kIn Exercises 35– 44, find Tt, Nt, a T , and a N at the given timet for the plane curve rt.35. rt ti 1 t 1 36. rt t 2 i 2t j,t j,37. rt t t 3 i 2t 2 j, t 138. rt t 3 4ti t 2 1j, t 0t 4P0, 4, 419. rt t, ln t, t, t 0 120. rt e t , 2 cos t, 2 sin t, t 0 0In Exercises 21 and 22, verify that the space curves intersect atthe given values of the parameters. Find the angle between thetangent vectors to the curves at the point of intersection.21. rt t 2, t 2 , 1 2 t, t 4us 1 2 sin2 s sin s, 1 1 2 sin2 s sin s,12 sin s cos s 1 2 s, s 0t 139. rt e t i e 2t j, t 040. rt e t i e t j tk, t 041. rt e t cos ti e t sin tj, t 242. rt a cos ti b sin tj, t 043. rt cos t t sin t, sin t t cos t,44. rt t sin t, 1 cos t, t t 0Circular Motion In Exercises 45–48, consider an objectmoving according to the position functionrt a cos t i a sin t j.45. Find Tt, Nt, a T , and a N .46. Determine the directions of T and N relative to the positionfunction r.47. Determine the speed of the object at any time t and explain itsvalue relative to the value of a T .48. If the angular velocity is halved, by what factor is a Nchanged?In Exercises 49–52, sketch the graph of the plane curve givenby the vector-valued function, and, at the point on the curvedetermined by rt 0 , sketch the vectors T and N. Note that Npoints toward the concave side of the curve.49.50.Functionrt ti 1 t jrt t 3 i tj51. rt 2 cos ti 2 sin tj52. rt 3 cos ti 2 sin tjIn Exercises 53–56, find Tt, Nt, a T , and a N at the given timet for the space curve rt. [ Hint: Find at, Tt, and a N . Solve forN in the equation at a T T a N N.]Function53.54.rt ti 2tj 3tkrt 4ti 4tj 2tkt 1t 255. rt ti t 2 j t2 t 12 k56. rt e t sin ti e t cos tj e t kIn Exercises 57 and 58, use a computer algebra system to graphthe space curve. Then find Tt, Nt, a T , and a N at the giventime t. Sketch Tt and Nt on the space curve.Function57. rt 4ti 3 cos tj 3 sin tkTimet 0 2t 0 1t 0 4t 0 Timet 0Timet 258. rt ti 3t 2 j t2 t 22 kt t 0

332460_1204.qxd 11/5/04 9:07 AM Page 865SECTION 12.4 Tangent Vectors and Normal Vectors 865Writing About Concepts59. Define the unit tangent vector, the principal unit normalvector, and the tangential and normal components ofacceleration.60. How is the unit tangent vector related to the orientation ofa curve? Explain.61. Describe the motion of a particle if the normal componentof acceleration is 0.62. Describe the motion of a particle if the tangential componentof acceleration is 0.63. Cycloidal Motion The figure shows the path of a particlemodeled by the vector-valued functionrt t sin t, 1 cos t.The figure also shows the vectors vtvt and atat atthe indicated values of t.yt =12t = 1(a) Find a and a at t 1 and t 3 2 , t 1,2 .T N(b) Determine whether the speed of the particle is increasing ordecreasing at each of the indicated values of t. Give reasonsfor your answers.64. Motion Along an Involute of a Circle The figure shows aparticle moving along a path modeled byThe figure also shows the vectors vt and at for t 1 andt 2.t = 1yt = 2t =rt cos t t sin t, sin t t cos t.32(a) Find a T and a N at t 1 and t 2.(b) Determine whether the speed of the particle is increasing ordecreasing at each of the indicated values of t. Give reasonsfor your answers.xxIn Exercises 65–70, find the vectors T and N, and the unitbinormal vector B T N, for the vector-valued function rtat the given value of t.65. rt 2 cos ti 2 sin tj t 66. rt ti t 2 j t32 k3 kxFigure for 65 Figure for 6667.68.t 0 2343−1zrt i sin tj cos tk,rt 2e t i e t cos tj e t sin tk,69. rt 4 sin ti 4 cos tj 2tk,70. rt 2 cos 2ti 2 sin 2tj tk,71. Projectile Motion Find the tangential and normal componentsof acceleration for a projectile fired at an angle with thehorizontal at an initial speed of v 0 . What are the componentswhen the projectile is at its maximum height?72. Projectile Motion Use your results from Exercise 71 to findthe tangential and normal components of acceleration for aprojectile fired at an angle of 45 with the horizontal at aninitial speed of 150 feet per second. What are the componentswhen the projectile is at its maximum height?73. Projectile Motion A projectile is launched with an initialvelocity of 100 feet per second at a height of 5 feet and at anangle of 30with the horizontal.(a) Determine the vector-valued function for the path of theprojectile.(b) Use a graphing utility to graph the path and approximatethe maximum height and range of the projectile.(c) Find vt, vt, and at.(d) Use a graphing utility to complete the table.(e) Use a graphing utility to graph the scalar functions a T anda N . How is the speed of the projectile changing when a Tand have opposite signs?a N3yx2t 0 41t 0 11zt 0 0t 0 3t 0 4t 0.5 1.0 1.5 2.0 2.5 3.0Speed2y

332460_1204.qxd 11/5/04 9:07 AM Page 866866 CHAPTER 12 Vector-Valued Functions74. Projectile Motion A projectile is launched with an initialvelocity of 200 feet per second at a height of 4 feet and at anangle of 45with the horizontal.(a) Determine the vector-valued function for the path of theprojectile.(b) Use a graphing utility to graph the path and approximatethe maximum height and range of the projectile.(c) Find vt, vt, and at.(d) Use a graphing utility to complete the table.t 0.5 1.0 1.5 2.0 2.5 3.0Speed75. Air Traffic Control Because of a storm, ground controllersinstruct the pilot of a plane flying at an altitude of 4 miles tomake a 90turn and climb to an altitude of 4.2 miles. Themodel for the path of the plane during this maneuver isrt 10 cos 10t, 10 sin 10t, 4 4t,where t is the time in hours and r is the distance in miles.(a) Determine the speed of the plane.(b) Use a computer algebra system to calculate a T and a N .Why is one of these equal to 0?76. Projectile Motion A plane flying at an altitude of 36,000 feetat a speed of 600 miles per hour releases a bomb. Find thetangential and normal components of acceleration acting on thebomb.77. Centripetal Acceleration An object is spinning at a constantspeed on the end of a string, according to the position functiongiven in Exercises 45–48.(a) If the angular velocity is doubled, how is the centripetalcomponent of acceleration changed?(b) If the angular velocity is unchanged but the length of thestring is halved, how is the centripetal component of accelerationchanged?78. Centripetal Force An object of mass m moves at a constantspeed v in a circular path of radius r. The force required toproduce the centripetal component of acceleration is called thecentripetal force and is given by F mv 2 r. Newton’s Law ofUniversal Gravitation is given by F GMmd 2 , where d is thedistance between the centers of the two bodies of masses M andm, and G is a gravitational constant. Use this law to show thatthe speed required for circular motion is v GMr.0 ≤ t ≤ 120Orbital Speed In Exercises 79–82, use the result of Exercise 78to find the speed necessary for the given circular orbit aroundEarth. Let GM 9.56 10 4 cubic miles per second per second,and assume the radius of Earth is 4000 miles.79. The orbit of a space shuttle 100 miles above the surface of Earth80. The orbit of a space shuttle 200 miles above the surface of Earth81. The orbit of a heat capacity mapping satellite 385 miles abovethe surface of Earth82. The orbit of a SYNCOM satellite r miles above the surface ofEarth that is in geosynchronous orbit [The satellite completesone orbit per sidereal day (approximately 23 hours, 56 minutes),and therefore appears to remain stationary above a pointon Earth.]True or False? In Exercises 83 and 84, determine whether thestatement is true or false. If it is false, explain why or give anexample that shows it is false.83. If a car’s speedometer is constant, then the car cannot beaccelerating.84. If a N 0 for a moving object, then the object is moving in astraight line.85. A particle moves along a path modeled byrt coshbti sinhbtjwhere b is a positive constant.(a) Show that the path of the particle is a hyperbola.(b) Show that at b 2 rt.86. Prove that the principal unit normal vector N points toward theconcave side of a plane curve.87. Prove that the vector Tt is 0 for an object moving in a straightline.88. Prove that a N v a.v89. Prove that a N a 2 a T2 .Putnam Exam Challenge90. A particle of unit mass moves on a straight line under the actionof a force which is a function fv of the velocity v of theparticle, but the form of this function is not known. A motion isobserved, and the distance x covered in time t is found to beconnected with t by the formula x at bt 2 ct 3 , where a,b, and c have numerical values determined by observation ofthe motion. Find the function fv for the range of v covered bythe experiment.This problem was composed by the Committee on the Putnam Prize Competition.©The Mathematical Association of America. All rights reserved.