Observation of Shock Waves in a Strongly Interacting ... - Physics

More documents

Recommendations

Info

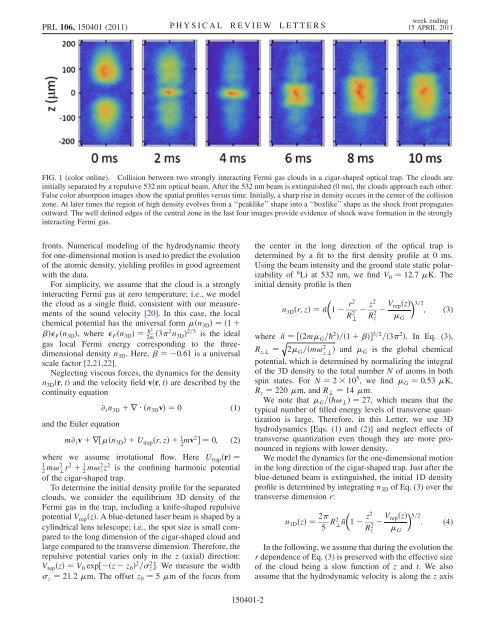
PRL 106, 150401 (2011) PHYSICAL REVIEW LETTERSweek ending15 APRIL 2011FIG. 1 (color online). Collision between two strongly interacting Fermi gas clouds in a cigar-shaped optical trap. The clouds areinitially separated by a repulsive 532 nm optical beam. After the 532 nm beam is extinguished (0 ms), the clouds approach each other.False color absorption images show the spatial profiles versus time. Initially, a sharp rise in density occurs in the center of the collisionzone. At later times the region of high density evolves from a ‘‘peaklike’’ shape into a ‘‘boxlike’’ shape as the shock front propagatesoutward. The well defined edges of the central zone in the last four images provide evidence of shock wave formation in the stronglyinteracting Fermi gas.fronts. Numerical modeling of the hydrodynamic theoryfor one-dimensional motion is used to predict the evolutionof the atomic density, yielding profiles in good agreementwith the data.For simplicity, we assume that the cloud is a stronglyinteracting Fermi gas at zero temperature; i.e., we modelthe cloud as a single fluid, consistent with our measurementsof the sound velocity [20]. In this case, the localchemical potential has the universal form ðn 3D Þ¼ð1 þÞ F ðn 3D Þ, where F ðn 3D Þ¼ @22m ð32 n 3D Þ 2=3 is the idealgas local Fermi energy corresponding to the threedimensionaldensity n 3D . Here, ¼ 0:61 is a universalscale factor [2,21,22].Neglecting viscous forces, the dynamics for the densityn 3D ðr;tÞ and the velocity field vðr;tÞ are described by thecontinuity equationand the Euler equation@ t n 3D þrðn 3D vÞ¼0 (1)m@ t v þr½ðn 3D ÞþU trap ðr; zÞþ 1 2 mv2 Š¼0; (2)where we assume irrotational flow. Here U trap ðrÞ ¼12 m!2 ? r2 þ 1 2 m!2 zz 2 is the confining harmonic potentialof the cigar-shaped trap.To determine the initial density profile for the separatedclouds, we consider the equilibrium 3D density of theFermi gas in the trap, including a knife-shaped repulsivepotential V rep ðzÞ. A blue-detuned laser beam is shaped by acylindrical lens telescope; i.e., the spot size is small comparedto the long dimension of the cigar-shaped cloud andlarge compared to the transverse dimension. Therefore, therepulsive potential varies only in the z (axial) direction:V rep ðzÞ ¼V 0 exp½ ðz z 0 Þ 2 = 2 zŠ. We measure the width z ¼ 21:2 m. The offset z 0 ¼ 5 m of the focus fromthe center in the long direction of the optical trap isdetermined by a fit to the first density profile at 0 ms.Using the beam intensity and the ground state static polarizabilityof 6 Li at 532 nm, we find V 0 ¼ 12:7 K. Theinitial density profile is thenn 3D ðr; zÞ ¼~n 1r 2R 2 ?z 2R 2 zV rep ðzÞ G 3=2;(3)where ~n ¼½ð2m G =@ 2 Þ=ð1 þ ÞŠ 3=2 =ð3 2 Þ. In Eq. (3),qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiR z;? ¼ 2 G =ðm! 2 z;? Þ and G is the global chemicalpotential, which is determined by normalizing the integralof the 3D density to the total number N of atoms in bothspin states. For N ¼ 2 10 5 , we find G ¼ 0:53 K,R z ¼ 220 m, and R ? ¼ 14 m.We note that G =ð@! ? Þ¼27, which means that thetypical number of filled energy levels of transverse quantizationis large. Therefore, in this Letter, we use 3Dhydrodynamics [Eqs. (1) and (2)] and neglect effects oftransverse quantization even though they are more pronouncedin regions with lower density.We model the dynamics for the one-dimensional motionin the long direction of the cigar-shaped trap. Just after theblue-detuned beam is extinguished, the initial 1D densityprofile is determined by integrating n 3D of Eq. (3) over thetransverse dimension r:n 1D ðzÞ ¼ 2 5 R2 ? ~n 1z 2R 2 zV rep ðzÞ G 5=2:(4)In the following, we assume that during the evolution ther dependence of Eq. (3) is preserved with the effective sizeof the cloud being a slow function of z and t. We alsoassume that the hydrodynamic velocity is along the z axis150401-2
PRL 106, 150401 (2011) PHYSICAL REVIEW LETTERSweek ending15 APRIL 2011and does not depend on r. Then the subsequent timeevolution of the density follows the quasi-1D nonlinearhydrodynamic equations:@ t n ¼ @ z ðnvÞ; (5)@ t v ¼ @ z v22 þ Cn2=5 þ 1 2 !2 zz 2 þ @ zðn@ z vÞ; (6)nwhere C ¼ 1 2 !2 ? l2 ? ð15 2 l ?Þ 2=5 ð1 þ Þ 3=5 and l ? ¼pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi@=ðm! ? Þ is the oscillator length. For brevity, we haveomitted the subscript 1D in Eqs. (5) and (6). The last‘‘viscosity’’ term in Eq. (6) is added phenomenologicallyto describe dissipative effects. For the strongly interacting1D fluid, is the effective kinematic viscosity, which hasa natural scale @=m. It is the only fitting parameter in thetheory [9].For our previous sound wave experiments [20], weobserved nonlinear (amplitude-dependent) propagationwithout shock waves. By reducing the density perturbation,we observed linear propagation. In this regime, one canexpand the differential equations (5) and (6) around anequilibrium density configuration n 0 ðzÞ in a harmonictrap. By defining nðz; tÞ n 0 ðzÞþnðz; tÞ, the linearizedevolution equation for nðz; tÞ (neglecting viscosity) is 2C@ 2 t n ¼ @ z n 0 @ z5m n ð3=5Þ0n : (7)With a flat background density, i.e., constant n 0 , with G ¼ Cn 2=50 , Eq. (7) reduces to @ 2 t n ¼ c 2 @ 2 zn with thepsound velocity c ¼ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi2 G =5m, in agreement with predictions[23,24].To compare the numerical solutions of Eqs. (5) and (6)with experiment, we note that the images are taken after anadditional free expansion for 1.5 ms, during which n 1Dcontinues to slowly evolve in the axial potential of the biasmagnetic field, i.e., ! z ! ! Mz ¼ 2 20:4 Hz. We assumethat, during this expansion, the transverse densityprofiles keep the same form, but the radius increases withtime. Then n 3D ðr; zÞ !n 3D ðr=b ? ;zÞ=b 2 ? , where b ?ðtÞ is atransverse scale factor, which obeys €b ? ¼ ! 2 ? b 7=3? , withb ? ð0Þ ¼1 and b _ ? ð0Þ ¼0 [2,25,26]. Since the 3D pressurescales as n 5=34=33D, the 1D pressure scales as b? . This leads toa simple modification of Eq. (6): C ! CðtÞ ¼C=b 4=3? ðtÞ.We numerically integrate Eqs. (5) and (6) by using themeasured values of the trap frequencies, the atom number,and the offset, depth, and width of the repulsive potential.In the numerical simulation, we create and load a densityarray as well as a velocity array with grid spacing z . Theinitial velocity is set to zero. The simulation then updatesthe density and velocity field in discrete time steps taccording to Eqs. (5) and (6). The 1D density profiles arecalculated as a function of time after the repulsive potentialis extinguished. Figure 2 shows the predictions and theFIG. 2 (color online). 1D density profiles divided by the totalnumber of atoms versus time for two colliding strongly interactingFermi gas clouds. The normalized density is in units of10 2 =m per particle. Red dots show the measured 1D densityprofiles. Black curves show the simulation, which uses themeasured trap parameters and the number of atoms, with thekinetic viscosity as the only fitting parameter.data, which are in very good agreement. For the simulationcurves shown in the figure, we use a grid of 150 points.To check for numerical consistency, we also employ asmoothed-particle-hydrodynamics [27] approach, wherethe fluid is described by discrete pseudoparticles. Theresults obtained indeed coincide with the discretized-gridapproach described above.As shown in Fig. 2, we observe a dramatic evolution forthe density of the gas. During the collision, a distinct andstable density peak forms at the point of collision in thecenter of the trap [28]. The density gradient at the side ofthe central peak increases from its onset until 3ms,at which point the gradient reaches its maximum value.A large gradient at the edge of the collision zone is maintainedthroughout the rest of the experiment. For mostof the data, we find relatively small deviations from thesimulation. The largest deviation occurs at 4 ms, where themaximum density of the observed central peak exceedsthat of the simulation by ’ 20%.The steep density gradients observed in Fig. 1 suggestshock wave formation. A deeper analysis of the simulation150401-3
Page 1: PRL 106, 150401 (2011) PHYSICAL REV

Observation of Shock Waves in a Strongly Interacting ... - Physics

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?