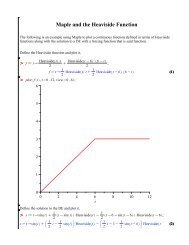
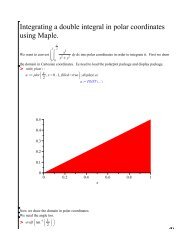
Spring 2008 Math 273 Review for Final Exam 1. review all earlier ...

• 12.5 14: ∇f = 2i + 4j − 6k ⇒ (D u f) P0 = ∇f · u = 03(h) Find direction and magnitude of maximum rate of change 18, 19• 12.5 18: ∇f(1, 0) = 2j ⇒ u = j. f increases most rapidly in the direction of jand decreases most rapidly in the direction of −j.(i) 12.6 Linearisation of f(x, y) 29, 41; Computing error 47;(j) Find the equation of the tangent plane to the surface z = f(x, y) at the pointP = (x 0 , y 0 , z 0 ). 10, 11• 12.6 10: z = 1(k) 12.7 Given z = f(x, y). Find the relative maximum and minimum points andsaddle points (if there are any). Show why they are max or min. 14, 17, 19, 27,47. Chapter review 60, 61• 12.7 14: Local minimum of f(x, y) is f(1, 0) = 0• 12.7 60: Saddle point at f(0, −1) = 2(l) 12.8 Use method of Lagrange multipliers to find extrema satisfying one givenconstraint. In particular, find point closest to a given surface. 17, 195. Chapter 13(a) 13.1 Double integrals over a given rectangular region. Focus on deciding whichorder of integration is simpler. 10, 16, 17, 18• 13.1 10:• 13.1 16:• 13.1 18:∫ 1 ∫ 20∫∫R∫∫R1xye x dydx =y sin(x + y) dA =xye xy2 dA =∫ 1∫ 2 ∫ 1032 xex dx = 3 20∫ 0 ∫ π0−π0y sin(x + y) dydx = 4xye xy2 dydx = 1 2 (e2 − 3)(b) 13.2 Double integrals over general regions: Focus on finding new limits when reversingorder of integration. 18, 19, 20, 27, 28, 29• 13.2 18:∫ 1 ∫ √ 1−y0 1−ydxdy

• 13.2 20:• 13.2 28:∫ 2 ∫ ln x1 0∫ 2 ∫ 4−x 200dydxxe 2y ∫ 44 − y dydx =0∫ √ 4−y0xe 2y4 − y dxdy = e8 − 144(c) 13.3 Average value of a function, area of a region 12, 15• 13.3 12:∫ 2 ∫ y+2−1y 2 dxdy = 9 2(d) 13.4 Converting integrals from rectangular to polar coordinates and evaluatingpolar integrals 3, 7, 14, 18, 19• 13.4 14:∫ 2 ∫ 0• 13.4 18: Area = 20xy−√1−(y−1) 2 dxdy =2∫ π/6 ∫ 1+cos θ01∫ ππ/2∫ 2 sin θ0r drdθ = 12πsin 2 θ cos θr 4 drdθ = − 4 5(e) 13.5 (No changing order of integration) • triple integrals 14, 27, 32• 13.5 14: 16/3• 13.5 32: Volume =∫ 2 ∫ √ 4−x ∫ 2 3−x−2 − √ 4−x 2 0dzdydx = 12π(f) 13.7 Focus on spherical coordinates. • 37, 38, Chapter review 33• 13.7 38: Volume =(g) 13.8 Computing Jacobians∫ 2π ∫ π/2 ∫ 20π/30ρ 2 sin φ dρdφdθ = 8π 3i. • Find the Jacobian of the transformation from (x, y) −→ (u, v) given thatx = e u+v and y = e u−vJacobian = −2e 2uii. • Find the Jacobian of the transformation from (x, y) −→ (u, v) given thatx = 5u − v and y = u + 3vJacobian = 16iii. • Find the Jacobian of the transformation from (x, y) −→ (u, v) given thatx = uv and y = u v

5Jacobian = −2uviv. • Find the Jacobian of the transformation from (x, y, z) −→ (u, v, w) giventhatx = v + w 2 and y = w + u 2 and z = u + v 2Jacobian = −2 + 8uvw6. Chapter 14: Vector Fields(a) (14.3 1 — 6) Determine whether F is a conservative field.(b) (14.3 1 — 6) Compute div and curl for a vector field F.• 14.3 1: Conservative. div F = 0, curl F = 0• 14.3 2: Conservative. div F = −xy sin z, curl F = 0• 14.3 3: Not conservative. div F = 0, curl F = −2i• 14.3 4: Not conservative. div F = 0, curl F = 2k• 14.3 5: Not conservative. div F = 0, curl F = −k• 14.3 6: Conservative. div F = e x cos y − e x cos y + 1, curl F = 0(c) 14.3 Find a potential function for F. 7 — 9• 14.3 8:f(x, y, z) = xy + xz + yz + C