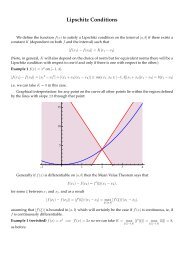
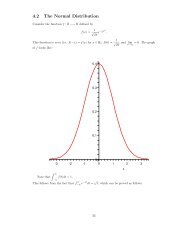
MATH10040: Numbers and Functions Homework 1: Solutions

Solution:(a) Let p, q be rational numbers. So there are integers a, b, c, d suchthat p = a/b and q = c/d. Thereforepq = a b · cd = acbdwhich is a rational number since ac, bd ∈ Z.(b) Again, let p = a/b and q = c/d where a, b, c, d ∈ Z (and b, d ≠ 0).Thenp ± q = a b ± c d = adbd ± bc ad ± bc=bd bdis rational since bd, ad ± bc ∈ Z.(c) Let c = a + b, d = ab.Suppose, FTSOC, that c is rational. Since a is rational, it followsfrom (b) that c − a = b is rational: a contradiction. So c isirrational.Similarly, suppose FTSOC that d is rational. Now a ≠ 0 isrational, hence 1/a is rational. By (b), it follows that (1/a)·d = bis rational: again, a contradiction.4. We will show later that √ 2 is an irrational number. Give an exampleof two distinct positive irrational numbers a and b which have theproperty that a + b is rational. Prove your assertions.Solution: Take a = √ 2 and b = 2 − √ 2.First we show that b is irrational: √ 2 is irrational, hence so is − √ 2.Since 2 is rational, b = 2 + (− √ 2) is irrational by part (c) of the lastexercise.Note that b > 0 since 2 > √ 2. Also b ≠ a.(Proof: b = a =⇒ √ 2 + √ 2 = 2 =⇒ 2 √ 2 = 2 =⇒ √ 2 = 1, acontradiction.)So a, b are distinct postive irrational numbers whose sum is 2.5. Prove by induction on n that for all natural numbers n ≥ 11 2 + 2 2 + · · · + n 2 =n(n + 1)(2n + 1).6Solution: For n = 1 the statement readsand so is true.1 2 =1 · 2 · (2 + 1)6= 6 6 = 1