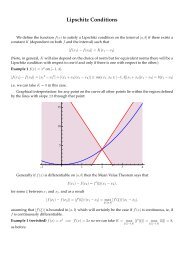
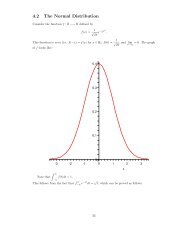
Chapter 5. Mathematics in the time of Descartes and Fermat

(1777-1855) is known as one of the greatest mathematicians of all time. His early famerests on his book Disquisitiones arithmeticae, published in 1801 when he was just 24. Thebook contains all the work on number theory that he had done up to that time. It includesthe definitive result on the construction of regular polygons using ruler and compass alone.It had been known since the time of Euclid and earlier that we can construct a regular(equilateral) triangle, a regular pentagon, a regular hexagon, and any regular polygonhaving 2 n sides, using a ruler and compass alone. No further constructions of such figureswere known. Using his work on the roots of the polynomial x n −1 (which are of course thecomplex roots of unity cos(2kπ/n)+i sin(2kπ/n)), Gauss proved the following fundamentalresult:• Let p be a prime number. A regular polygon of p sides is constructible by ruler andcompass alone if and only if p is a Fermat prime. A regular polygon of n sides isconstructible by ruler and compass alone if and only if, in the prime factorization ofn, we have n = 2 t p 1 p 2 · · · p r , where p 1 , . . . , p r are different Fermat primes.It is said that Gauss’s discovery of the construction by ruler and compass of the regular17-sided polygon in 1796, when he was only 18, was the crucial event that decided him onhis career as a mathematician and not as a philologist. The actual construction is a littletechnical but Gauss’s work is considered to be the most original addition to the study ofEuclidian geometry for over two thousand years.His success in showing the non-existence of non-trivial integral solutions to theseDiophantine equations must have led Fermat to believe that the method of descent couldlikewise prove that there are no non-zero integers x, y and z that satisfyx n + y n = z n ,whenever n is an integer greater than 2. He certainly left a note in the margin of his copyof the Arithmetica stating that he had found such a solution. Nobody was able to makethe method of descent apply in the cases where n > 4, and we must presume that Fermatwas wrong in his claim. In fact, attempts to verify the truth of Fermat’s Last Theorem(as the claim became known) led to the development of a vast generalization of arithmeticknown as algebraic number theory, in which the theory of primes and unique factorizationis carried over to certain special types of complex number. Even this was not enough toprove Fermat’s Last Theorem in general, as the complete proof by Andrew Wiles in 1995used techniques of algebraic geometry and modular form theory.10