Algebra II Unit 1: Polynomial, Rational, and Radical Relationships ...

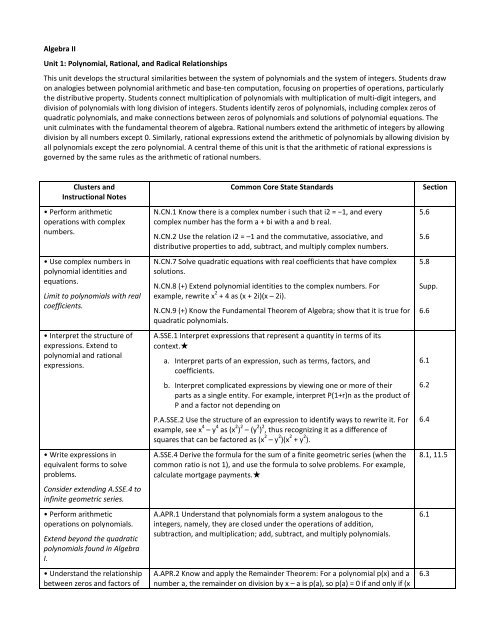
Algebra IIUnit 1: Polynomial, Rational, and Radical RelationshipsThis unit develops the structural similarities between the system of polynomials and the system of integers. Students drawon analogies between polynomial arithmetic and base-ten computation, focusing on properties of operations, particularlythe distributive property. Students connect multiplication of polynomials with multiplication of multi-digit integers, anddivision of polynomials with long division of integers. Students identify zeros of polynomials, including complex zeros ofquadratic polynomials, and make connections between zeros of polynomials and solutions of polynomial equations. Theunit culminates with the fundamental theorem of algebra. Rational numbers extend the arithmetic of integers by allowingdivision by all numbers except 0. Similarly, rational expressions extend the arithmetic of polynomials by allowing division byall polynomials except the zero polynomial. A central theme of this unit is that the arithmetic of rational expressions isgoverned by the same rules as the arithmetic of rational numbers.Clusters andInstructional Notes• Perform arithmeticoperations with complexnumbers.• Use complex numbers inpolynomial identities andequations.Limit to polynomials with realcoefficients.• Interpret the structure ofexpressions. Extend topolynomial and rationalexpressions.• Write expressions inequivalent forms to solveproblems.Consider extending A.SSE.4 toinfinite geometric series.• Perform arithmeticoperations on polynomials.Extend beyond the quadraticpolynomials found in AlgebraI.• Understand the relationshipbetween zeros and factors ofCommon Core State StandardsN.CN.1 Know there is a complex number i such that i2 = −1, and everycomplex number has the form a + bi with a and b real.N.CN.2 Use the relation i2 = –1 and the commutative, associative, anddistributive properties to add, subtract, and multiply complex numbers.N.CN.7 Solve quadratic equations with real coefficients that have complexsolutions.N.CN.8 (+) Extend polynomial identities to the complex numbers. Forexample, rewrite x 2 + 4 as (x + 2i)(x – 2i).N.CN.9 (+) Know the Fundamental Theorem of Algebra; show that it is true forquadratic polynomials.A.SSE.1 Interpret expressions that represent a quantity in terms of itscontext.★a. Interpret parts of an expression, such as terms, factors, andcoefficients.b. Interpret complicated expressions by viewing one or more of theirparts as a single entity. For example, interpret P(1+r)n as the product ofP and a factor not depending onP.A.SSE.2 Use the structure of an expression to identify ways to rewrite it. Forexample, see x 4 – y 4 as (x 2 ) 2 – (y 2 ) 2 , thus recognizing it as a difference ofsquares that can be factored as (x 2 – y 2 )(x 2 + y 2 ).A.SSE.4 Derive the formula for the sum of a finite geometric series (when thecommon ratio is not 1), and use the formula to solve problems. For example,calculate mortgage payments.★A.APR.1 Understand that polynomials form a system analogous to theintegers, namely, they are closed under the operations of addition,subtraction, and multiplication; add, subtract, and multiply polynomials.A.APR.2 Know and apply the Remainder Theorem: For a polynomial p(x) and anumber a, the remainder on division by x – a is p(a), so p(a) = 0 if and only if (xSection5.65.65.8Supp.6.66.16.26.48.1, 11.56.16.3

polynomials.• Use polynomial identities tosolve problems.This cluster has manypossibilities for optionalenrichment, such as relatingthe example in A.APR.4 to thesolution of the system u 2 +v 2 =1,v = t(u+1), relating the Pascaltriangle property of binomialcoefficients to (x+y) n+1 =(x+y)(x+y) n , deriving explicitformulas for the coefficients,or proving the binomialtheorem by induction.• Rewrite rational expressionsThe limitations on rationalfunctions apply to the rationalexpressions in A.APR.6.A.APR.7 requires the generaldivision algorithm forpolynomials.• Understand solvingequations as a process ofreasoning and explain thereasoning.Extend to simple rational andradical equations.• Represent and solveequations and inequalitiesgraphically.Include combinations of linear,polynomial, rational, radical,absolute value, andexponential functions.• Analyze functions usingdifferent representations.Relate F.IF.7c to therelationship between zeros ofquadratic functions and theirfactored forms– a) is a factor of p(x).A.APR.3 Identify zeros of polynomials when suitable factorizations areavailable, and use the zeros to construct a rough graph of the functiondefined by the polynomial.A.APR.4 Prove polynomial identities and use them to describe numericalrelationships. For example, the polynomial identity (x 2 + y 2 ) 2 = (x 2 – y 2 ) 2 +(2xy) 2 can be used to generate Pythagorean triples.A.APR.5 (+) Know and apply the Binomial Theorem for the expansion of (x +y)n in powers of x and y for a positive integer n, where x and y are anynumbers, with coefficients determined for example by Pascal’s Triangle.A.APR.6 Rewrite simple rational expressions in different forms; write a(x)/b(x)in the form q(x) + r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomialswith the degree of r(x) less than the degree of b(x), using inspection, longdivision, or, for the more complicated examples, a computer algebra system.A.APR.7 (+) Understand that rational expressions form a system analogous tothe rational numbers, closed under addition, subtraction, multiplication, anddivision by a nonzero rational expression; add, subtract, multiply, and dividerational expressions.A.REI.2 Solve simple rational and radical equations in one variable, and giveexamples showing how extraneous solutions may arise.A.REI.11 Explain why the x-coordinates of the points where the graphs of theequations y = f(x) and y = g(x) intersect are the solutions of the equation f(x) =g(x); find the solutions approximately, e.g., using technology to graph thefunctions, make tables of values, or find successive approximations. Includecases where f(x) and/or g(x) are linear, polynomial, rational, absolute value,exponential, and logarithmic functions.★F.IF.7 Graph functions expressed symbolically and show key features of thegraph, by hand in simple cases and using technology for more complicatedcases.★c. Graph polynomial functions, identifying zeros when suitablefactorizations are available, and showing end behavior.6.46.86.37.5, 9.6Donethroughout6.1 Ext.,6.2

Unit 2: Trigonometric FunctionsBuilding on their previous work with functions, and on their work with trigonometric ratios and circles in Geometry,students now use the coordinate plane to extend trigonometry to model periodic phenomena.Clusters andInstructional Notes• Extend the domain oftrigonometric functions usingthe unit circle.• Model periodic phenomenawith trigonometric functions.• Prove and applytrigonometric identities.An Algebra II course with anadditional focus ontrigonometry could include the(+) standard F.TF.9: Prove theaddition and subtractionformulas for sine, cosine, andtangent and use them to solveproblems. This could belimited to acute angles inAlgebra II.Common Core State StandardsF.TF.1 Understand radian measure of an angle as the length of the arc on theunit circle subtended by the angle.F.TF.2 Explain how the unit circle in the coordinate plane enables theextension of trigonometric functions to all real numbers, interpreted asradian measures of angles traversed counterclockwise around the unit circle.F.TF.5 Choose trigonometric functions to model periodic phenomena withspecified amplitude, frequency, and midline.★F.TF.8 Prove the Pythagorean identity sin2(θ) + cos2(θ) = 1 and use it to findsin (θ), cos (θ), or tan (θ), given sin (θ), cos (θ), or tan (θ), and the quadrant ofthe angle.Section13.2,13.313.2,13.313.4-13.814.1

Unit 3: Modeling with FunctionsIn this unit students synthesize and generalize what they have learned about a variety of function families. They extendtheir work with exponential functions to include solving exponential equations with logarithms. They explore the effects oftransformations on graphs of diverse functions, including functions arising in an application, in order to abstract the generalprinciple that transformations on a graph always have the same effect regardless of the type of the underlying function.They identify appropriate types of functions to model a situation, they adjust parameters to improve the model, and theycompare models by analyzing appropriateness of fit and making judgments about the domain over which a model is a goodfit. The description of modeling as “the process of choosing and using mathematics and statistics to analyze empiricalsituations, to understand them better, and to make decisions” is at the heart of this unit. The narrative discussion anddiagram of the modeling cycle should be considered when knowledge of functions, statistics, and geometry is applied in amodeling context.Clusters and InstructionalNotes• Create equations thatdescribe numbers orrelationships.For A.CED.1, use all availabletypes of functions to createsuch equations, including rootfunctions, but constrain tosimple cases. While functionsused in A.CED.2, 3, and 4 willoften be linear, exponential, orquadratic the types ofproblems should draw frommore complex situations thanthose addressed in Algebra I.For example, finding theequation of a line through agiven point perpendicular toanother line allows one to findthe distance from a point to aline. Note that the examplegiven for A.CED.4 applies toearlier instances of thisstandard, not to the currentcourse.• Interpret functions that arisein applications in terms of acontext.Emphasize the selection of amodel function based onbehavior of data and context.Common Core State StandardsA.CED.1 Create equations and inequalities in one variable and use them tosolve problems. Include equations arising from linear and quadratic functions,and simple rational and exponential functions.A.CED.2 Create equations in two or more variables to represent relationshipsbetween quantities; graph equations on coordinate axes with labels andscales.A.CED.3 Represent constraints by equations or inequalities, and by systems ofequations and/or inequalities, and interpret solutions as viable or non-viableoptions in a modeling context. For example, represent inequalities describingnutritional and cost constraints on combinations of different foods.A.CED.4 Rearrange formulas to highlight a quantity of interest, using the samereasoning as in solving equations. For example, rearrange Ohm’s law V = IR tohighlight resistance R.F.IF.4 For a function that models a relationship between two quantities,interpret key features of graphs and tables in terms of the quantities, andsketch graphs showing key features given a verbal description of therelationship. Key features include: intercepts; intervals where the function isincreasing, decreasing, positive, or negative; relative maximums andminimums; symmetries; end behavior; and periodicity.★F.IF.5 Relate the domain of a function to its graph and, where applicable, tothe quantitative relationship it describes. For example, if the function h(n)gives the number of person-hours it takes to assemble n engines in a factory,then the positive integers would be an appropriate domain for the function.★F.IF.6 Calculate and interpret the average rate of change of a function(presented symbolically or as a table) over a specified interval. Estimate therate of change from a graph.★SectionsCh. 5 toCh. 91.31.42.22.32.4

• Analyze functions usingdifferent representations.Focus on applications and howkey features relate tocharacteristics of a situation,making selection of aparticular type of functionmodel appropriate.• Build a function that modelsa relationship between twoquantities.Develop models for morecomplex or sophisticatedsituations than in previouscourses.• Build new functions fromexisting functions.Use transformations offunctions to find models asstudents consider increasinglymore complex situations.For F.BF.3, note the effect ofmultiple transformations on asingle graph and the commoneffect of each transformationacross function types.Extend F.BF.4a to simplerational, simple radical, andsimple exponential functions;connect F.BF.4a to F.LE.4.• Construct and comparelinear, quadratic, andexponential models and solveproblems.Consider extending this unit toinclude the relationshipbetween properties oflogarithms and properties ofexponents, such as theconnection between theproperties of exponents andthe basic logarithm propertythat log xy = log x +log y.F.IF.7 Graph functions expressed symbolically and show key features of thegraph, by hand in simple cases and using technology for more complicatedcases.★b. Graph square root, cube root, and piecewise-defined functions,including step functions and absolute value functions.e. Graph exponential and logarithmic functions, showing intercepts andend behavior, and trigonometric functions, showing period, midline,and amplitude.F.IF.8 Write a function defined by an expression in different but equivalentforms to reveal and explain different properties of the function.F.IF.9 Compare properties of two functions each represented in a differentway (algebraically, graphically, numerically in tables, or by verbaldescriptions). For example, given a graph of one quadratic function and analgebraic expression for another, say which has the larger maximum.F.BF.1 Write a function that describes a relationship between two quantities.*b. Combine standard function types using arithmetic operations. Forexample, build a function that models the temperature of a coolingbody by adding a constant function to a decaying exponential, andrelate these functions to the model..F.BF.3 Identify the effect on the graph of replacing f(x) by f(x) + k, k f(x), f(kx),and f(x + k) for specific values of k (both positive and negative); find the valueof k given the graphs. Experiment with cases and illustrate an explanation ofthe effects on the graph using technology. Include recognizing even and oddfunctions from their graphs and algebraic expressions for them.F.BF.4 Find inverse functions.a. Solve an equation of the form f(x) = c for a simple function f that has aninverse and write an expression for the inverse. For example, f(x) = 2 x 3or f(x) = (x+1)/(x-1) for x ≠ 1.F.LE.4 For exponential models, express as a logarithm the solution to a b ct = dwhere a, c, and d are numbers and the base b is 2, 10, or e; evaluate thelogarithm using technology.Ch. 5 toCh. 92.2 Ext13.4 to13.6

Unit 4: Inferences and Conclusions from DataIn this unit, students see how the visual displays and summary statistics they learned in earlier grades relate to differenttypes of data and to probability distributions. They identify different ways of collecting data—including sample surveys,experiments, and simulations—and the role that randomness and careful design play in the conclusions that can be drawn.Clusters and Instructional Notes Common Core State Standards Sections• Summarize, represent, and interpret data on asingle count or measurement variable.While students may have heard of the normaldistribution, it is unlikely that they will have priorexperience using it to make specific estimates. Buildon students’ understanding of data distributions tohelp them see how the normal distribution uses areato make estimates of frequencies (which can beexpressed as probabilities). Emphasize that onlysome data are well described by a normaldistribution.• Understand and evaluate random processesunderlying statistical experiments.For S.IC.2, include comparing theoretical andempirical results to evaluate the effectiveness of atreatment.• Make inferences and justify conclusions fromsample surveys, experiments, and observationalstudies.In earlier grades, students are introduced to differentways of collecting data and use graphical displaysand summary statistics to make comparisons. Theseideas are revisited with a focus on how the way inwhich data is collected determines the scope andnature of the conclusions that can be drawn fromthat data. The concept of statistical significance isdeveloped informally through simulation as meaninga result that is unlikely to have occurred solely as aresult of random selection in sampling or randomassignment in an experiment. For S.IC.4 and 5, focuson the variability of results from experiments—thatis, focus on statistics as a way of dealing with, noteliminating, inherent randomness.• Use probability to evaluate outcomes of decisions.Extend to more complex probability models. Includesituations such as those involving quality control, ordiagnostic tests that yield both false positive andfalse negative results.S.ID.4 Use the mean and standard deviation of a dataset to fit it to a normal distribution and to estimatepopulation percentages. Recognize that there are datasets for which such a procedure is not appropriate. Usecalculators, spreadsheets, and tables to estimate areasunder the normal curve.S.IC.1 Understand statistics as a process for makinginferences about population parameters based on arandom sample from that population.S.IC.2 Decide if a specified model is consistent withresults from a given data-generating process, e.g., usingsimulation. For example, a model says a spinning coinfalls heads up with probability 0.5. Would a result of 5tails in a row cause you to question the model?S.IC.3 Recognize the purposes of and differences amongsample surveys, experiments, and observationalstudies; explain how randomization relates to each.S.IC.4 Use data from a sample survey to estimate apopulation mean or proportion; develop a margin oferror through the use of simulation models for randomsampling.S.IC.5 Use data from a randomized experiment tocompare two treatments; use simulations to decide ifdifferences between parameters are significant.S.IC.6 Evaluate reports based on data.S.MD.6 (+) Use probabilities to make fair decisions (e.g.,drawing by lots, using a random number generator).S.MD.7 (+) Analyze decisions and strategies usingprobability concepts (e.g., product testing, medicaltesting, pulling a hockey goalie at the end of a game).Ch. 12Ch. 12Supp.