Chapter 1 Conservation of Mass - Light and Matter

More documents

Recommendations

Info

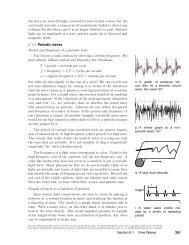
i / Two balls start from rest, and roll from A to B by different paths. field. If the plane can start from 10 km up, what is the maximum amount of time for which the dive can last? ⊲ Based on data about acceleration and distance, we want to find time. Acceleration is the second derivative of distance, so if we integrate the acceleration twice with respect to time, we can find how position relates to time. For convenience, let’s pick a coordinate system in which the positive y axis is down, so a=g instead of −g. a = g 84 Chapter 2 Conservation of Energy v = gt + constant (integrating) = gt (starts from rest) y = 1 2 gt2 + constant (integrating again) Choosing our coordinate system to have y = 0 at t = 0, we can make the second constant of integration equal zero as well, so � 2y t = g � 2 · 10000 m = 10 m/s 2 � = 2000 s 2 = 40 s (to one sig. fig.) Note that if we hadn’t converted the altitude to units of meters, we would have gotten the wrong answer, but we would have been alerted to the problem because the units inside the square root wouldn’t have come out to be s 2 . In general, it’s a good idea to convert all your data into SI (meter-kilogram-second) units before you do anything with them. High road, low road example 9 ⊲ In figure i, what can you say based on conservation of energy about the speeds of the balls when the reach point B? What does conservation of energy tell you about which ball will get there first? Assume friction doesn’t convert any mechanical energy to heat or sound energy. ⊲ Since friction is assumed to be negligible, there are only two forms of energy involved: kinetic and gravitational. Since both balls start from rest, and both lose the same amount of gravitational energy, they must have the same kinetic energy at the end, and therefore they’re rolling at the same speed when they reach B. (A subtle point is that the balls have kinetic energy both because they’re moving through space and because they’re spinning as they roll. These two types of energy must be in fixed
proportion to one another, so this has no effect on the conclusion.) Conservation of energy does not, however, tell us anything obvious about which ball gets there first. This is a general problem with applying conservation laws: conservation laws don’t refer directly to time, since they are statements that something stays the same at all moments in time. We expect on intuitive grounds that the ball that goes by the lower ramp gets to B first, since it builds up speed early on. Buoyancy example 10 ⊲ A cubical box with mass m and volume V = b 3 is submerged in a fluid of density ρ. How much energy is required to raise it through a height ∆y? ⊲ As the box moves up, it invades a volume V ′ = b 2 ∆y previously occupied by some of the fluid, and fluid flows into an equal volume that it has vacated on the bottom. Lowering this amount of fluid by a height b reduces the fluid’s gravitational energy by ρV ′ gb = ρgb 3 ∆y, so the net change in energy is ∆E = mg∆y − ρgb 3 ∆y = (m − ρV )g∆y . In other words, it’s as if the mass of the box had been reduced by an amount equal to the fluid that otherwise would have occupied that volume. This is known as Archimedes’ principle, and it is true even if the box is not a cube, although we’ll defer the more general proof until page 202 in chapter 3. If the box is less dense than the fluid, then it will float. A simple machine example 11 ⊲ If the father and son on the seesaw in figure k start from rest, what will happen? ⊲ Note that although the father is twice as massive, he is at half the distance from the fulcrum. If the seesaw was going to start rotating, it would have to be losing gravitational energy in order to gain some kinetic energy. However, there is no way for it to gain or lose gravitational energy by rotating in either direction. The change in gravitational energy would be ∆U = ∆U1 + ∆U2 = g(m1∆y1 + m2∆y2) , but ∆y1 and ∆y2 have opposite signs and are in the proportion of two to one, since the son moves along a circular arc that covers the same angle as the father’s but has half the radius. Therefore ∆U = 0, and there is no way for the seesaw to trade gravitational energy for kinetic. j / How much energy is required to raise the submerged box through a height ∆y? k / A seesaw. l / The biceps muscle is a reversed lever. Section 2.1 Energy 85
Page 1 and 2: from rest with an acceleration of 1
Page 3 and 4: 41 Estimate the number of man-hours
Page 5 and 6: Chapter 1 Conservation of Mass It t
Page 7 and 8: y scientists who actually specializ
Page 9 and 10: yesterday’s. One way of stating a
Page 11 and 12: happens because the greater gravita
Page 13 and 14: m/s. From my point of view, the fri
Page 15 and 16: special “rest frame.” Since the
Page 17 and 18: derivative v = dx/dt is called the
Page 19 and 20: only certain values of mass are pos
Page 21 and 22: kind used, for example, to test des
Page 23 and 24: Chapter 2 Conservation of Energy Do
Page 25 and 26: Conservation of energy tells us ∆
Page 27 and 28: Although the story is picturesque a
Page 29 and 30: a symbols. kg · m2 1 J = 1 = 1 s 2
Page 31 and 32: since we don’t know how the perso
Page 33: elated to gravitational mass, but s
Page 37 and 38: lock in figure o/3. Even if the blo
Page 39 and 40: Water in a U-shaped tube example 13
Page 41 and 42: 2.2 Numerical Techniques Engineerin
Page 43 and 44: But by increasing n to ten thousand
Page 45 and 46: 17 ds = math.sqrt(dx**2+dy**2) # Py
Page 47 and 48: calculations and many false starts
Page 49 and 50: In one second, the satellite moves

Chapter 1 Conservation of Mass - Light and Matter

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?