population ecology ii - Biology

Estimating Population Density
Quadrat methods
Quadrat: a sampling area
of any shape
Quadrats can be contiguous
or random
Capture-recapture methods

Quadrat Methods
Mean density =
Total individuals
Total area of quadrats

Quadrat No. Individuals (y)
1 9
2 15
3 7
4 4
5 8
6 6
7 11
8 5
9 11
10 8
N = number of
quadrats
= 100
n = number of
quadrats
sampled
= 10

Sample Mean
Sample Variance
Sample Standard Deviation

Mean Density
Estimate Total Population
Estimate Variance of T

Capture-recapture methods
Key assumptions of the capturerecapture
method:
population closure
mark integrity
equal catchability

Marked animals in Marked animals in
second sample first sample
------------------------ = ----------------------------
Total caught in Total population size
second sample
5 / 20 = 16 / T
T = 64
Density = T / total area

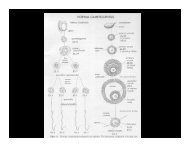
Dispersion: the spatial arrangement of
individuals within populations
Three patterns:
Uniform
Random
Aggregated
or clumped

Estimating Population Dispersion
Quadrat methods
Poisson Probability Distribution
Are individuals randomly distributed among
quadrats?
Distance methods

Poisson Probability Distribution
Let X = number of individuals in a quadrat
µ = population density
Expected value of X
Variance of X

Are moss shoots randomly distributed?

=[P(Y=0)]N
N

Poisson distribution and natural sampling
units
Are corn-borer larvae
randomly distributed among
corn stems?

Test Statistic

Variance-to-Mean Ratio is a measure of
dispersion
E(X) = µ Var(X) = µ
V/M = 1 Random dispersion
V/M < 1 Uniform dispersion
V/M > 1 Aggregated dispersion

The pattern of dispersion exhibited by a group of
organisms depends on the spatial scale on which the
organisms are studied

This association is clearly demonstrated by
the relationship between the V/M and
quadrat size
Caveat: If the true
pattern is random,
then the V/M is
unaffected by
quadrat size
Quadrat size V/M Ratio
10 0.939
15 1.057
20 0.996
25 1.134
30 1.393
35 1.567
40 1.634

Distance methods
F(r) = Pr(distance to nearest neighbor < r)
= probability that a circle of radius r is not empty
A= area of study region
N= number of points
r

Test for randomness
Refer Z to the Standard
Normal Probability
Distribution
Sample mean of nearest
neighbor distances