elementos de la teoria de tensiones y deformaciones - unne
elementos de la teoria de tensiones y deformaciones - unne
elementos de la teoria de tensiones y deformaciones - unne
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
ESTABILIDAD II CAPITULO III: ELEMENTOS DE LA TEORIA DE TENSIONES Y DEFORMACIONES<br />
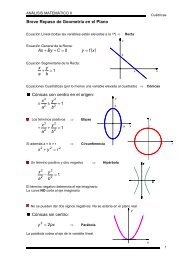
Para po<strong>de</strong>r enten<strong>de</strong>rnos con c<strong>la</strong>ridad al referirnos a <strong>la</strong>s <strong>tensiones</strong>, vamos a establecer ciertas<br />
convenciones:<br />
σ i : el subíndice i indicará al eje respecto <strong>de</strong>l cual <strong>la</strong>s <strong>tensiones</strong> normales son parale<strong>la</strong>s ( σ x, σ y, σ z ).<br />
Serán positivas cuando produzcan tracción.<br />
τ ij : el subíndice i indicará el vector normal al p<strong>la</strong>no don<strong>de</strong> actúan <strong>la</strong>s <strong>tensiones</strong> tangenciales, y el subíndice<br />
j indicará el eje al que resultan parale<strong>la</strong>s ( τ xy, τ xz, τ yz, τ yx, τ zx, τ zy ).<br />
Tanto <strong>la</strong>s <strong>tensiones</strong> normales como <strong>la</strong> tangenciales varían punto a punto en el interior <strong>de</strong> un<br />
cuerpo, por lo tanto, <strong>de</strong>bemos tener presente que <strong>la</strong>s <strong>tensiones</strong> quedan expresadas como funciones:<br />
s = s (x,y,z) t = t (x,y,z)<br />
3.2 EQUILIBRIO DE UN PRISMA ELEMENTAL<br />
Consi<strong>de</strong>remos, como en <strong>la</strong> figura 3.3, un punto A correspondiente a un sólido sujeto a <strong>tensiones</strong>,<br />
punto que hacemos coincidir con el origen <strong>de</strong> coor<strong>de</strong>nadas; y tres p<strong>la</strong>nos perpendicu<strong>la</strong>res que pasan<br />
por el punto, coinci<strong>de</strong>ntes con los p<strong>la</strong>nos coor<strong>de</strong>nados. Supongamos a<strong>de</strong>más un segundo punto B<br />
<strong>de</strong>l mismo sólido, <strong>de</strong> coor<strong>de</strong>nadas dx, dy y dz..<br />
Admitiremos que <strong>la</strong>s funciones que <strong>de</strong>finen <strong>la</strong>s <strong>tensiones</strong> en los puntos <strong>de</strong>l sólido son continuas<br />
y <strong>de</strong>rivables. Las <strong>tensiones</strong> que actúan en los p<strong>la</strong>nos que pasan por B pue<strong>de</strong>n <strong>de</strong>finirse como <strong>la</strong>s<br />
que actúan en los p<strong>la</strong>nos paralelos pasantes por A mas el correspondiente incremento. Así tendremos,<br />
s x<br />
por ejemplo, s x y sx<br />
+ dx tomando como incremento el primer término <strong>de</strong>l <strong>de</strong>sarrollo en serie<br />
x<br />
<strong>de</strong> Taylor.<br />
/2005 2