CONTROL AUTOM´ATICO I

CONTROL AUTOMÁTICO I
SOLUCIÓN Segundo certamen
TODAS LAS RESPUESTAS DEBEN ESTAR JUSTIFICADAS.
TODAS LAS VARIABLES QUE USE EN SUS RESPUESTAS DEBEN ESTAR EXPLÍCI-
TAMENTE DEFINIDAS.
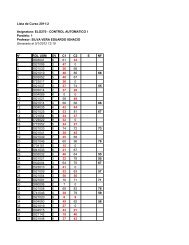
Problema 2.1 (100 pts.). En un lazo de control realimentado se sabe que los diagramas de Bode
de G o (s)C(s) son los que se muestran en la figura 2.1. Se sabe que G o (s)C(s) tiene sólo polos en el
SPI abierto.
20
Magnitud [dB]
0
−20
−40
−60
−80
10 −2 10 −1 10 0 10 1 10 2
Fase [o]
0
−50
−100
−150
−200
10 −2 10 −1 10 0 10 1 10 2
Figura 1: Diagramas de Bode, problema 2.1
2.1.1 [30 pts.] Dibuje el diagrama de Nyquist correspondiente. Debe ser cualtitativamente correcto
y deben justificarse los rasgos claves del diagrama, a partir de la información que se puede
extraer de los diagramas de Bode.
2.1.2 [30 pts.] Demuestre que el lazo cerrado es estable (suponga que no ha habido cancelaciones
de polos ni ceros de la planta, en el SPD cerrado).
2.1.3 [40 pts.]¿Qué retardo habría que agregar al lazo para llevarlo al punto crítico de estabilidad?.
Si se agregara ese retardo crítico, ¿cuál sería la frecuencia de la oscilación?

Solución
2.1.1 De los diagramas de Bode, y del hecho que G o (s)C(s) es estable, notamos lo siguiente:
La magnitud decrece monótonamente a medida que ω crece, llegando a cero para ω = ∞.
La magnitud es mayor que 1 en ω = 0; sin embargo, es menor que 1 cuando el diagrama
polar de G o (jω)C(jω) ingresa al tercer cuadrante.
El ángulo es negativo ∀ω ≥ 0, y se hace monótonamente más negativo a medida que ω
crece
El ángulo va desde 0 a −π [rad], recorriendo los cuadrantes 4 y 3, cuando ω va desde
0a∞. Así, el diagrama polar de G o (jω)C(jω) nunca cruza el eje real negativo.
Con estas observaciones podemos proponer el siguiente diagrama de Nyquist
1.5
Nyquist Diagram
1
0.5
Imaginary Axis
0
−0.5
−1
−1.5
−1.5 −1 −0.5 0 0.5 1 1.5
Real Axis
Figura 2: Diagrama de Nyquist aproximado, problema 2.1
2.1.2 Tanto del diagrama de Nyquist, como de los diagramas de Bode se aprecia que el margen de
ganancia es infinito, y que el margen de fase es positivo. En consecuencia el lazo es estable.
2.1.3 El retardo crítico es el que hace G o (jω c )C(jω c )=−1, paraalgún ω c ∈ R + , es decir, que
hace la magnitud igual a 1, y la fase igual a −π. Para analizar este caso, consideremos los
diagramas de Bode que se muestran en la Figura 2.1. Allí se aprecia que el margen de fase
(y el de ganancia) puede ser llevado a cero si aumentamos la fase en −110 [o] app. en otras
palabras, el retardo crítico, τ c se puede calcular a partir de
ω c τ c = 110 pi
180 ⇐⇒ τ c = 11
18ω c
π
Se observa que ω c ≈ 1; por lo cual τ c ≈ 11
18 π.
Ahora bien, a la frecuencia ω c , se cumple que G o (jω c )C(jω c )=−1. Por otro lado, los polos
del lazo cerrado cumplen con G o (s)C(s) =−1, lo cual indica que precisamente hay polos en
±jω c .Así, la oscilación sería de frecuencia angular ω c .
2

20
Magnitud [dB]
0
−20
−40
−60
−80
10 −2 10 −1 10 0 10 1 10 2
Fase [o]
0
−50
−100
−150
−200
10 −2 10 −1 10 0 10 1 10 2
Figura 3: Diagramas de Bode, con margen de fase indicado, problema 2.1
Problema 2.2 (100 pts.). Suponga que G o (s) =
1
s(s + 1)
2.2.1 [50 pts.] ¿Se puede estabilizar un lazo cerrado con un controlador de la familia PID, que
sólo contiene el modo integrativo?
2.2.2 [50 pts.] Demuestre que esta planta es controlable en un lazo cerrado estable con un controlador
PI. Proponga valores para K p y T r .
Solución
2.2.1 El controlador I tiene la función de transferencia C(s) = K I
, por lo que el polinomio característico
del lazo cerrado tendría la
s
expresión
A cl (s) =s 3 + s 2 + K I
De allí se observa que el lazo es inestable, porque en ese polinomio falta el término lineal en
s.
2.2.2 En este caso
3

(
C(s) =K p 1 + 1 )
= K ps + K I
T r s s
La estabilidad se puede probar usando el algoritmo de Routh que arroja las condiciones
Así, por ejemplo, se pueden elegir T r = 2 y K p = 2
K p >K I ⇐⇒ T r >1 (1)
K I >0⇐⇒ K p >0 (2)
Problema 2.3 (100 pts.). Suponga que el modelo nominal de una planta estable es el mostrado
en la figura 2.3.
8
6
4
DIAGRAMA DE NYQUIST
EJE IMAGINARIO
2
0
−2
−4
−6
−8
−10 −8 −6 −4 −2 0 2 4 6 8
EJE REAL
Figura 4: Diagrama de Nyquist, problema 2.3
2.3.1 [40 pts.] Si esa planta se controla con un controlador proporcional de ganancia unitaria
¿Cuántos polos tiene el lazo cerrado en el SPD?
4

2.3.2 [60 pts.] ¿Qué ganancia K p de un controlador proporcional elegiría para que el margen de
ganancia sea de 6 [dB] ?Sepidesólo cálculos aproximados
Solución
2.3.1 En este caso, dado que G o (s)C(s) =G o (s) es estable, no hay polos del lazo abierto en el
SPD, es decir, P = 0. Observando el diagrama se aprecia que encierra el punto (−1; 0) dos
veces en sentido de reloj, es decir N =−2. En consecuencia Z = P − N = 2, es decir, el lazo
cerrado tiene dos polos en el SPD abierto.
2.3.2 El margen requerido implica que el diagrama polar debe cruzar el eje real negativo en
(−0,5; 0). Si consideramos que con ganancia 1 cruza el eje real negativo en (−8,5; 0) aprox.,
entonce se requiere que
K p = 0,5/8,5 = 1/17
Problema 2.4 (100 pts.). Una planta estable tiene un modelo cuya incertidumber multiplicativa
satisface
2ω
|G ∆ (jω)| ≤ √
ω2 + 100
2.4.1 [50 pts.] Determine el máximo ancho de banda de T o que asegura estabilidad robusta.
2.4.2 [50 pts.] Determine el máximo ancho de banda que asegure
|G ∆ (jω)T o (jω)| ≤ 0,8
Sugerencia: SI NECESITA DIAGRAMAS DE BODE, USE APROXIMACIONES ASINTÓTI-
CAS.
Solución
Este problema puede resolverse en forma analítica o en forma gráfica (como se estudió en clases).
Para mayor variedad se presenta ahora la solución analítica
2.4.1 La condición de estabilidad robusta se asegura si |T o (jω)G ∆ (jω)|

2.4.2 En este caso, repetimos el procedimiento, aunque numéricamente el cálculo de ω c es diferente,
como se aprecia de las fórmulas
|T o (jω)| ≤ 0,8
√
ω2 + 100
2ω
1
2 = 0,16ω2 + 100
ω 2 =⇒ ω c =
4
√
0, 34
Esto indica que para asegurar la condición de robustez dada, el ancho de banda debería ser
4
menor o igual que √ .
0, 34
6