4.4 VALORES EXTREMOS Le sugerimos al lector, estudiar ...

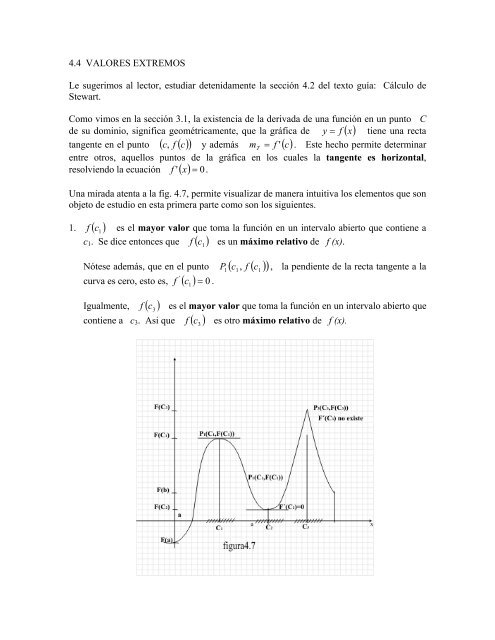
4.4 VALORES EXTREMOSLe sugerimos al lector, estudiar detenidamente la sección 4.2 del texto guía: Cálculo deStewart.Como vimos en la sección 3.1, la existencia de la derivada de una función en un punto Cde su dominio, significa geométricamente, que la gráfica de y = f ( x)tiene una rectatangente en el punto ( c, f () c ) y además m T= f ' ( c). Este hecho permite determinarentre otros, aquellos puntos de la gráfica en los cuales la tangente es horizontal,resolviendo la ecuación f ' x = 0.( )Una mirada atenta a la fig. 4.7, permite visualizar de manera intuitiva los elementos que sonobjeto de estudio en esta primera parte como son los siguientes.( )1. f c 1es el mayor valor que toma la función en un intervalo abierto que contiene ac1. Se dice entonces que f ( ) es un máximo relativo de f (x).Nótese además, que en el punto P1( c1, f ( c1))'curva es cero, esto es, f ( c ) = 0 .Igualmente,f( ) c 31c 1, la pendiente de la recta tangente a laes el mayor valor que toma la función en un intervalo abierto que( )contiene a c3. Asi que f es otro máximo relativo de f (x).c 3

Sin embargo, en el punto P ( c f ( ))3 3, c3, la derivada de f (x) no existe (se presentaun pico), lo cual indica que en un punto de máximo relativo no necesariamente debeanularse la derivada.2. f ( c 2) es el menor valor que toma la función en un intervalo abierto que contiene acf es un mínimo relativo de f (x). De la misma2. Se dice, entonces que ( c 2)'manera que en el caso anterior en el punto P ( c f ( )), ( c ) = 02 2, c2f .3. Si se comparan ahora, todos los valores que toma la función f (x) en el intervalo [a,b], se puede notar de la figura que f (a) es el menor valor y que f es el mayor( ) c 3valor. f (a) y f se llaman respectivamente el mínimo absoluto y el máximoabsoluto de f (x) en [a, b].Los conceptos antes mencionados, serán presentados aquí en forma sencilla, así comolas condiciones necesarias y suficientes para la existencia de extremos relativos. Alfinal, se enunciará un teorema y se dará un procedimiento para determinar los extremosabsolutos de una función continua en un intervalo cerrado (Método del intervalocerrado).2( )c 3Definiciones:Sea f una función de variable real y sea c ∈ D f (Dominio de f). Entonces:i. f(c) es un VALOR MÁXIMO RELATIVO DE f, si existe un intervalo abiertoI que contiene a c tal que:f ( c ) ≥ f ( x ) para todo x ∈ Iii.iii.iv.f(c) es un VALOR MÍNIMO RELATIVO DE f, si existe un intervalo abiertoI que contiene a c tal que:f ( c ) ≤ f ( x ) para todo x ∈ If(c) es un VALOR MÁXIMO ABSOLUTO DE f, en un intervalo I, abiertoo cerrado, si:f ( c ) ≥ f ( x ) para todo x ∈ If(c) es un VALOR MÍNIMO ABSOLUTO DE f, en un intervalo I, abierto ocerrado, si:f ( c ) ≤ f ( x ) para todo x ∈ Iv. A los valores máximos y mínimos relativos de una función se les llama:EXTREMOS RELATIVOS.A los valores máximos y mínimos absolutos de una función se les llama:EXTREMOS ABSOLUTOS.

Observaciones:i. Puede ocurrir que un extremo absoluto sea simultáneamente extremo relativo, comof en la fig. 4.8.sucede por ejemplo con ( )c 3ii.El llamado “teorema de los valores extremos” enunciado al final de la sección,garantiza la existencia de extremos absolutos para una función continua en unintervalo cerrado [a, b]. A pesar de que estos valores son únicos, la función puedetomarlos en diferentes puntos del intervalo. (Ver el ejercicio de la sección 9.10).