Tema 3. Señales y sistemas en tiempo discreto. Introducción: ⢠Las ...
Tema 3. Señales y sistemas en tiempo discreto. Introducción: ⢠Las ...
Tema 3. Señales y sistemas en tiempo discreto. Introducción: ⢠Las ...
- No tags were found...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
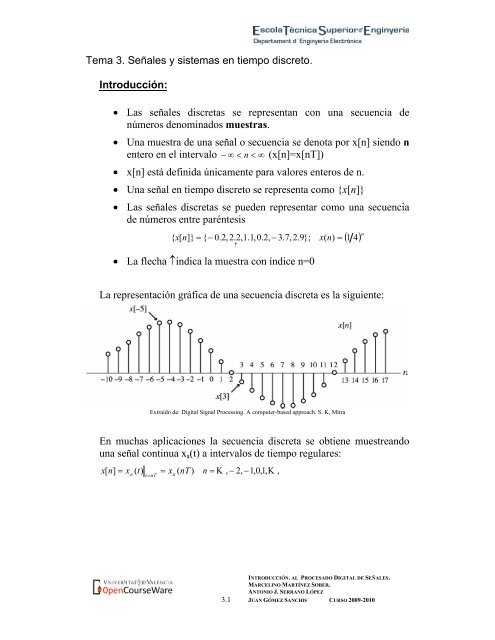
<strong>Tema</strong> <strong>3.</strong> Señales y <strong>sistemas</strong> <strong>en</strong> <strong>tiempo</strong> <strong>discreto</strong>.Introducción:• <strong>Las</strong> señales discretas se repres<strong>en</strong>tan con una secu<strong>en</strong>cia d<strong>en</strong>úmeros d<strong>en</strong>ominados muestras.• Una muestra de una señal o secu<strong>en</strong>cia se d<strong>en</strong>ota por x[n] si<strong>en</strong>do n<strong>en</strong>tero <strong>en</strong> el intervalo − ∞ < n < ∞ (x[n]=x[nT])• x[n] está definida únicam<strong>en</strong>te para valores <strong>en</strong>teros de n.• Una señal <strong>en</strong> <strong>tiempo</strong> <strong>discreto</strong> se repres<strong>en</strong>ta como {x[n]}• <strong>Las</strong> señales discretas se pued<strong>en</strong> repres<strong>en</strong>tar como una secu<strong>en</strong>ciade números <strong>en</strong>tre paréntesis{ x[n]}= { − 0.2, 2.2,1.1,0.2, − <strong>3.</strong>7, 2.9}; x(n)= ( 1 4) n• La flecha ↑indica la muestra con índice n=0↑La repres<strong>en</strong>tación gráfica de una secu<strong>en</strong>cia discreta es la sigui<strong>en</strong>te:Extraído de: Digital Signal Processing. A computer-based approach. S. K, MitraEn muchas aplicaciones la secu<strong>en</strong>cia discreta se obti<strong>en</strong>e muestreandouna señal continua x a (t) a intervalos de <strong>tiempo</strong> regulares:x[ n]= x ( t)= x ( nT ) n = Κ , − 2, −1,0,1,Κ ,=atnTaINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>1 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Extraído de: Digital Signal Processing. A computer-based approach. S. K, MitraT es el período de muestreo y su inversa se d<strong>en</strong>omina frecu<strong>en</strong>cia demuestreo. Si T está <strong>en</strong> segundos las unidades de la frecu<strong>en</strong>cia de muestreoson ciclos por segundo o Hertzios.Indep<strong>en</strong>di<strong>en</strong>tem<strong>en</strong>te de que la secu<strong>en</strong>cia {x[n]} se haya obt<strong>en</strong>ido pormuestreo o no, se dice que x[n] es la n-ésima muestra de la secu<strong>en</strong>cia.Si todos los valores de la secu<strong>en</strong>cia {x[n]} son reales se dice que lasecu<strong>en</strong>cia es real, <strong>en</strong> otro caso se dice que se trata de una secu<strong>en</strong>ciacompleja.Una secu<strong>en</strong>cia compleja {x[n]} puede escribirse como{ x[n]}= { x [ n]}j{x [ n]}re+si<strong>en</strong>do x re[n]y x im[n]las partes reales e imaginarias de la secu<strong>en</strong>cia {x[n]}El complejo conjugado de una secu<strong>en</strong>cia se d<strong>en</strong>ota porEj. Secu<strong>en</strong>cia Real:{ x [ n]}= {cos0.25n}Ej Secu<strong>en</strong>cia Compleja:{ y[n]}= { ej0.3n} = {cos0.3n+{ y re[ n]}= {cos0.3n};{ y im[ n]}= {sin 0.3n}{ x*[n]}= { x [ n]}− j{x [ n]}rej sin 0.3n}= {cos0.3n}+ j{sin 0.3n}− .3La secu<strong>en</strong>cia { w[n]}= {cos0.3n}− j{sin 0.3n}= { ej0 n } es la conjugada de y [] n ,es decir { w [ n]}= { y *[ n]}Una señal discreta se dice que es finita o de longitud finita si está definidaúnicam<strong>en</strong>te <strong>en</strong> un intervalo finito N1 ≤ n ≤ N2con − ∞ < N1, N2< ∞ yN ≤ .1N 2La longitud o duración de una secu<strong>en</strong>cia es N = N − N 1.imim2 1+INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>2 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Desplazami<strong>en</strong>to temporal: y[ n]= x[n − N ] (N>0: Retardo, N
DE BLOQUES e indica las operaciones realizadas y el s<strong>en</strong>tido de flujo delos datos.Ej:Extraído de: Digital Signal Processing. A computer-based approach. S. K, Mitray[ n]= α1x[n]+ α2x[n −1]+ α3x[n − 2] + α4x[n − 3]Modificación de la frecu<strong>en</strong>cia de muestreo:Dada una secu<strong>en</strong>cia x[n] muestreada a una frecu<strong>en</strong>cia F T nos permiteobt<strong>en</strong>er una secu<strong>en</strong>cia y[n] muestreada a una frecu<strong>en</strong>cia F T’'FTLa relación <strong>en</strong>tre frecu<strong>en</strong>cias es: R =FTSi R>1 se habla de INTERPOLACIÓNSi R
INTERPOLACIÓNSi increm<strong>en</strong>tamos la frecu<strong>en</strong>cia de muestreo por un factor L>1, si<strong>en</strong>do L un<strong>en</strong>tero, insertamos L-1 ceros <strong>en</strong>tre muestras consecutivas.x u⎧ x[n / L],n = 0, ± L,± 2L,Λ[ n]= ⎨⎩ 0, <strong>en</strong> otro caso1Entrada1Salida0.80.80.60.60.40.4Amplitud0.20−0.2Amplitud0.20−0.2−0.4−0.4−0.6−0.6−0.8−0.8−10 10 20 30 40 50n−10 10 20 30 40 50nPosteriorm<strong>en</strong>te mediante un proceso de filtrado las muestras de valor cerose sustituirán por valores interpolados <strong>en</strong>tre las muestras exist<strong>en</strong>tes.DIEZMADOSi decrem<strong>en</strong>tamos la frecu<strong>en</strong>cia de muestreo por un factor M>1, si<strong>en</strong>do Mun <strong>en</strong>tero, tomamos una de cada M muestras de la señal original ydescartamos las M-1 intermedias.y [ n]= x[nM ]EntradaSalidaAmplitud10.80.60.40.20−0.2−0.4−0.6−0.8−10 10 20 30 40 50nAmplitud10.80.60.40.20−0.2−0.4−0.6−0.8−10 10 20 30 40 50nINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>7 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Clasificación de secu<strong>en</strong>cias<strong>Las</strong> secu<strong>en</strong>cias se pued<strong>en</strong> clasificar at<strong>en</strong>di<strong>en</strong>do a diversos criteriosSimetría:SECUENCIA CONJUGADA SIMÉTRICA: x[ n]= x*[−n]x[0] es un número real. Si x[n] es REAL se dice que se trata de unasecu<strong>en</strong>cia PAR.Ej. Secu<strong>en</strong>cia PARExtraído de: Digital Signal Processing. A computer-based approach. S. K, MitraSECUENCIA CONJUGADA ANTISIMÉTRICA: x[ n]= −x*[ −n]x[0] es un número IMAGINARIO PURO. Si x[n] es real se dice que setrata de una secu<strong>en</strong>cia IMPAR, <strong>en</strong> este caso x[0]=0.Ej. Secu<strong>en</strong>cia IMPARExtraído de: Digital Signal Processing. A computer-based approach. S. K, MitraCualquier secu<strong>en</strong>cia se puede poner como suma de dos secu<strong>en</strong>cias unaconjugada simétrica y otra conjugada antisimétricax[ n]= x [ n]x [ n]x csx cacs+ca1[ n]=n2( x[n]+ x *[ − ])1[ n]=n2( x[n]− x *[ − ])INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>8 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Si particularizamos para secu<strong>en</strong>cias reales, la propiedad nos dice quecualquier secu<strong>en</strong>cia real se puede poner como suma de una secu<strong>en</strong>cia par yotra imparx[ n]= x [ n]x [ n]par+imparEjemplo:x parx impar1[ n]=n2( x[n]+ x[− ])1[ n]=n2( x[n]− x[− ])Consideremos la secu<strong>en</strong>cia{ g[n]}= {0, 1+j4,−2+j3,4−j2,−5−j6,− j2,3}↑{ g * [ n]}= {0, 1−j4,−2−j3,4+j2,−5+j6,j2,↑3}{ g * [ −n]}= {3, j2,−5+j6,4+j 2, −2−j3,1−j4,↑La secu<strong>en</strong>cia conjugada simétrica es:1gcs[n]}= { g[n]+ g *[ −n]}= {1.5,21ca[n]}= { g[n]− g *[ −n]}= { −2{ 0.5+j3,−<strong>3.</strong>5+j4.5,4, −<strong>3.</strong>5−j 4.5, 0.5−j3,{ g 1.5, 0.5+j,1.5−j1.5,− j2,−1.5−j1.5,−0.5+j,Se puede verificar fácilm<strong>en</strong>te que g [ n]= g*[ −n]y g [ n]= −g*[ −n]cs cs ca ca0}↑↑1.5}1.5}PeriodicidadUna secu<strong>en</strong>cia x[n] se dice que es periódica si se verifica quex [ n]= x[n ± N ]. El m<strong>en</strong>or valor de N que verifica esta propiedad sed<strong>en</strong>omina período fundam<strong>en</strong>tal.Extraído de: Digital Signal Processing. A computer-based approach. S. K, MitraINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>9 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Si no se verifica la propiedad anterior se dice que la secu<strong>en</strong>cia esaperiódicaINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>10 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Señales de <strong>en</strong>ergía y de pot<strong>en</strong>ciaEnergía de una secu<strong>en</strong>cia:E∑ ∞ 2x= x[n]n=−∞Una secu<strong>en</strong>cia infinita puede t<strong>en</strong>er <strong>en</strong>ergía finita o no. Una secu<strong>en</strong>cia finitasiempre ti<strong>en</strong>e <strong>en</strong>ergía finita.x(n)= 1,3,5 , E = 36Ejemplos:{ }↑x(n)= 0.5nx(n)= u(n)u(n)E = ∞E = 2Pot<strong>en</strong>cia media de una secu<strong>en</strong>cia aperiódica:PK12x= lim+ ∑ x[n]K →∞ 2K1n=−KSi definimos la Energía de una secu<strong>en</strong>cia <strong>en</strong> un intervalo finitoK2Ex, K= ∑ x n]n=−K1Px= lim EK x.KK →∞ 2 + 1− K ≤ n ≤ K ,[ podemos expresar la pot<strong>en</strong>cia media comoPara una secu<strong>en</strong>cia periódica de período N se define la Pot<strong>en</strong>cia mediaN121como: ∑ − Px= x[n]Nn=0La pot<strong>en</strong>cia media de una secu<strong>en</strong>cia infinita puede ser finita o infinita.Ejemplo: Consideremos la secu<strong>en</strong>cia causaln⎧3(−1), n ≥ 0x[n]= ⎨⎩ 0, n < 0Ex∞∞2n2 2[] n = 3( −1) = 3 = ∞= ∑ x ∑ ∑n= −∞n=0n=01 ⎛ ⎞ 9( + 1)= lim ⎜9∑ KKPx1⎟= lim = 4.5K → ∞ 2K+ 1K →∞⎝ = 0 ⎠ 2 Kn+ 1∞Una señal de Energía Infinita y Pot<strong>en</strong>cia media finita se dice que es unaseñal de Pot<strong>en</strong>cia. Por ejemplo una señal periódica.Una señal de Energía Finita y Pot<strong>en</strong>cia media cero se dice que es una señalde Energía. Ej. Cualquier secu<strong>en</strong>cia de duración finitaINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>11 JUAN GÓMEZ SANCHIS CURSO 2009-2010
NOTA:Suma de términos de una progresión aritmética:SumaN2= ∑n=N1an5⎛ aN+ a1=⎜⎝ 2N2⎞⎟⎠( N − N + 1)Ej: Suma 2n−1= ⎜ ⎟( 5 − ( − 2)+ 1) = 16= ∑n=−22⎛ − 5 + 9 ⎞⎝ 2 ⎠1a n= a 0+ n ⋅ d :nSuma de términos de una progresión geométrica: an= a0 ⋅ r n ≥ 0N2aN⋅ r − a2 N1Suma = ∑an =si alguno de los límites,1 21N , N es infinito, paran= N r1−que se pueda realizar la suma es necesario que r ≤ 1Caso particulares:aSuma = ∑ ∞ 0an== 1−rn0Ej:Suma∞−1∞ −1−2−1n−2−1−2−1n−1−2( ) ( ) ( ) ( ) ( 3 ) − ( 3 ) − 2 ⋅= 2 ⋅ 3 ∑ 3 = 2 ⋅ 3=−1−11n=−2r = 3 < 1( 3 ) −1( 3 )∞= ∑ 2 3−n=−243= 3−15Otras clasificacionesSecu<strong>en</strong>cia acotada: x [ n]≤Ej. x[ n]= cos0.3πn ≤1B x< ∞Secu<strong>en</strong>cia absolutam<strong>en</strong>te sumable: ∑ ∞ x [ n]n=−∞Ej:n⎧0.3,y[n]= ⎨⎩ 0,n ≥ 0n < 0∑ ∞n=00.3n< ∞1= = 1.42857 < ∞1−0.3Secu<strong>en</strong>cia cuadrado sumable: ∑ ∞ x[n]= −∞n2< ∞INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>12 JUAN GÓMEZ SANCHIS CURSO 2009-2010
sin( 0.4πn)Ej: h[ n]= Esta serie no es absolutam<strong>en</strong>te sumable pero síπn2πcuadrado sumable.(La suma es ) 6Secu<strong>en</strong>cias Discretas BásicasImpulso unidad:1⎧1,δ [ n]= ⎨⎩0,n = 0n ≠ 0–4 –3 –2 –1 0 1 2 3 4 5 6nEscalón unidad:⎧1,u [ n]= ⎨⎩0,1n ≥ 0,(causal)n < 0–4 –3 –2 –1 0 1 2 3 4 5 6⎧0,n ≥ 0u [ −n−1]= ⎨ (anticausal)⎩1,n < 0⎧n,n ≥ 0Rampa unidad: r [ n]= n ⋅u(n)= ⎨⎩0,n < 0Rampa unidad5n4.54<strong>3.</strong>53r(n)2.521.510.50−5 0 5nINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>13 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Secu<strong>en</strong>cia sinusoidal: [ n]= Acos(ω n + φ)xoω 0 : frecu<strong>en</strong>cia angular <strong>en</strong> radianes/muestraA: Amplitudφ: FaseSecu<strong>en</strong>cia expon<strong>en</strong>cial:Si escribimosx[n]= A eejφ( σα = e( σ o + jωo), A =o + jωo) n= x [ n]+xxrereim[ n]=[ n]=j ximAeA ex[ n]= Aαn , −∞ < n < ∞jφy separamos <strong>en</strong> parte real e imaginaria[ n],obt<strong>en</strong>emos las secu<strong>en</strong>cias:Aeσ noσ nocos( ω n + φ)osin( ω n + φ)<strong>Las</strong> partes reales e imaginarias son sinusoides puras para σ o =0, creci<strong>en</strong>tespara σ o >0 y decreci<strong>en</strong>tes para σ o
<strong>Las</strong> secu<strong>en</strong>cias sinusoidales, Acos(ωon + φ)y las secu<strong>en</strong>cias expon<strong>en</strong>cialescomplejas B exp( jω on)son señales periódicas de período N si ωoN= 2πr,si<strong>en</strong>do N y r <strong>en</strong>teros; es decir, la frecu<strong>en</strong>cia digital es un número racionalrf =NSi no se cumple la relación anterior la secu<strong>en</strong>cia es no periódica. Ej:x [ n]= sin( 3n + φ).Secu<strong>en</strong>cia sinc:El secu<strong>en</strong>cia es muy utilizada <strong>en</strong> procesado de señales. Se trata de unasecu<strong>en</strong>cia no causal de duración infinitaRepres<strong>en</strong>tación se secu<strong>en</strong>cias arbitrarias mediante impulsos.Cualquier secu<strong>en</strong>cia discreta puede ser repres<strong>en</strong>tada como una sumak∑ == ∞k −∞ponderada de secu<strong>en</strong>cias impulso retardadas. x(n)= x(k)δ ( n − k)INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>15 JUAN GÓMEZ SANCHIS CURSO 2009-2010
x[ n]= 0.5δ[ n + 2] + 1.5δ[ n −1]− δ [ n − 2] + δ [ n − 4] + 0.75δ[ n − 6]Sistemas DiscretosUn sistema <strong>discreto</strong> procesa una secu<strong>en</strong>cia de <strong>en</strong>trada x[n] para obt<strong>en</strong>er unasecu<strong>en</strong>cia de salida y[n] modificando su propiedades (salvo el sistemay(n)=x(n)).El número de <strong>en</strong>tradas y salidas puede ser uno, como <strong>en</strong> un multiplicador, omúltiple como ocurre <strong>en</strong> un bloque sumador o modulador, retardo, etc.Ejemplos: y ( n)= 0.5( x(n)+ x(n −1))Sistema acumulador: La salida <strong>en</strong> un instante es la suma acumulada de lasnn−1muestras anteriores. y[n]= ∑ x[λ ] = ∑ x[λ]+ x[n]= y[n −1]+ x[n]λ= −∞ λ=−∞La relación <strong>en</strong>tre la <strong>en</strong>trada y la salida también se puede escribir como:−1y[n]= ∑ x[λ ] + ∑ x[λ]= y[−1]+ ∑ x[λ],λ=−∞nλ=0nλ=0n > 0y[-1] se d<strong>en</strong>omina condición inicial. La última expresión <strong>en</strong> la que n estádefinida para valores positivos se d<strong>en</strong>omina acumulador causalINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>16 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Promediado de M muestras (prom. móvil): la salida <strong>en</strong> un determinadoinstante es el promedio de la muestra actual y las M-1 muestras anteriores.M∑ − 11y [ n]= x[n − k]M k = 0Este tipo de promediado se utiliza para eliminar ruido de una señal.87d[n]s[n]x[n]87s[n]y[n]6565M=4Amplitude43Amplitude4231201−10 10 20 30 40 50Time index n00 10 20 30 40 50Time index nINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>17 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Clasificación de Sistemas DiscretosSistemas Lineales:Si y 1 [n] es la salida de un sistema ante una <strong>en</strong>trada x 1 [n] e y 2 [n] es la salidade un sistema ante una <strong>en</strong>trada x 2 [n], <strong>en</strong>tonces, si el sistema es lineal, anteuna <strong>en</strong>trada x[ n]= α x1[n]+ β x2[n], la salida es y[ n]= α y1[n]+ β y2[n]si<strong>en</strong>do α,β , x 1 [n] e x 2 [n] arbitrarios.Un sistema lineal verifica el principio de superposición.Ej1: Promediado de dos muestras: y [ n]= 0.5( x(n)+ x(n − 1) )Para dos <strong>en</strong>tradas arbitrarias las salidas serán:y1[ n]= 0.5( x1( n)+ x1(n −1)),y2[n]= 0.5( x2( n)+ x2( n −1))Para una <strong>en</strong>trada x[ n]= α x1[n]+ β x2[n]α, β ∈RLa salida es:y1[n]= 0.5( α x1[n]+ β x2[n]+ α x1[n −1]+ β x2[n −1]) == α(0.5( x ( n)+ x ( n −1)) + β (0.5( x ( n)+ x ( n −1)))1Luego el sistema es lineal1Ej2: AcumuladorPara dos <strong>en</strong>tradas arbitrarias las salidas serán:ynn1[ n]= ∑ x1[], y2[n]= ∑ x2λ=−∞λ=−∞λ [ λ]Para una <strong>en</strong>trada x[ n]= α x1[n]+ β x2[n]α, β ∈ RLa salida es:2nnn1nλ= −∞λ=−∞λ=−∞( α x [ λ ] + β x [ λ]) = α x [ λ]+ β x [ λ]= α y [ n]+ β y [ ]y[ n]= ∑2 ∑ ∑1212Luego el sistema es linealEj: Acumulador causalPara dos <strong>en</strong>tradas arbitrarias t<strong>en</strong>emos:ynn1[ n]= y1[−1]+ ∑ x1[λ ] y2[n]= y2[−1]+ ∑ x2[λ]λ=0λ=0Para una <strong>en</strong>trada x n]= α x [ n]+ β x [ ]La salida es:[1 2ny[n]= y[−1]+n∑λ=0( α x1 [ λ]+ β x2[λ])Si ahora calculamos α y n]+ β y [ ] obt<strong>en</strong>emos1[ 2n2INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>18 JUAN GÓMEZ SANCHIS CURSO 2009-2010
α y1[n]+ β y2[n]= α(y1[−1]+ ∑ x1[λ])+ β ( y2[−1]+ ∑ xnλ=0= ( α y1[−1]+ β y2[−1])+ ( α∑x1[λ]+ β∑nλ=0nλ=0x [ λ])2nλ=02[ λ])=Para que se verifique y[ n]= α y1[n]+ β y2[n]se debe cumplir,y[ −1]= α y1[−1]+ β y2[−1]para cualquier valor de α, β luego solo si lascondiciones iniciales son nulas el sistema será lineal <strong>en</strong> otro caso no loserá.2Ejercicio. Determina si el sistema y [ n]= x [ n]− x[n −1]x[n + 1]es lineal.INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>19 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Verificación de la linealidad de un sistema utilizando Matlab%Determina si el sistema y[n]=x[n]-2*x[n-1]-y[n-2] es lineal%Considera que las condiciones inciales son y[-1]=0.5;y[0]=2%Hemos considerado que el primer elem<strong>en</strong>to es el n=1%para evitar problemas de índices <strong>en</strong> Matlabclearclose allset(0, 'defaultaxesfontsize', 18)%G<strong>en</strong>eramos 2 secu<strong>en</strong>cia arbitrarias con los mismos elem<strong>en</strong>tosN=100;x1=0:N-1;x2=sin(2*pi*0.3*(1:N));%Condiciones inicialesy_1=0.5; y0=2;%G<strong>en</strong>eramos una secu<strong>en</strong>cia que sea una Comb. Lineal de ambasalfa=3; beta=0.5;x3=alfa*x1+beta*x2;%Hemos de calcular las salidas para las <strong>en</strong>tradas anteriores y1[n],y1[n] ey3[n]%Determinamos fuera del bucle la salida para índices problemáticos%n=1 y n=2%Para n=1n=1;y1(n)=x1(1)-2*0-y_1;%Análogo para el resto de <strong>en</strong>tradasy2(n)=x2(1)-2*0-y_1;y3(n)=x3(1)-2*0-y_1;%Para n=2n=2;y1(n)=x1(2)-2*x1(2-1)-y0;%Análogo para el resto de <strong>en</strong>tradasy2(n)=x2(2)-2*x2(2-1)-y0;y3(n)=x3(2)-2*x3(2-1)-y0;%Realizamos los cálculos para n>2for(n=3:N)y1(n)=x1(n)-2*x1(n-1)-y1(n-2);%Análogo para el resto de <strong>en</strong>tradasy2(n)=x2(n)-2*x2(n-1)-y2(n-2);y3(n)=x3(n)-2*x3(n-1)-y3(n-2);<strong>en</strong>d%Dibujamos las salidasplot(y3,'ro')hold onplot(alfa*y1+beta*y2,'g*');title('El sistema NO es lineal')xlabel('n')leg<strong>en</strong>d('y_3(n)','\alphay_1(n)+\betay_2(n)')INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>20 JUAN GÓMEZ SANCHIS CURSO 2009-2010
%Repetir el ejercicio considerando Condiciones iniciales (ccii) nulasINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>21 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Sistema: y [] n = x[] n − 2 x[ n −1] − y[ n − 2] ccii : y[ − 2] = 0.5 y[ −1] = 2200El sistema NO es linealy 3(n)αy 1(n)+βy 2(n)−20−40−60−80−100−120−140−1600 10 20 30 40 50 60 70 80 90 100nSi consideramos el mismo sistema con ccii nulas obt<strong>en</strong>emos.200El sistema SÍ es linealy 3(n)αy 1(n)+βy 2(n)−20−40−60−80−100−120−140−1600 10 20 30 40 50 60 70 80 90 100nINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>22 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Sistema invariante temporal.Un sistema que ante una <strong>en</strong>trada x 1 [n] produce una salida y 1 [n] esinvariante temporal si ante una <strong>en</strong>trada x[ n]= x1[n − no] la salida esy[ n]= y1[n − no].Es decir que si la secu<strong>en</strong>cia de <strong>en</strong>trada se retarda o adelanta, la secu<strong>en</strong>cia desalida estará retardada o adelantada ese mismo número de muestras.También podemos decir que la salida del sistema será la mismaindep<strong>en</strong>di<strong>en</strong>tem<strong>en</strong>te del instante <strong>en</strong> que se aplique la <strong>en</strong>trada.Ej.: Consideremos el sistema interpolador⎧ x[n / L],n = 0, ± L,± 2L,.....x u[ n]= ⎨para una <strong>en</strong>trada retardada x1[n]= x[n − no]⎩ 0, <strong>en</strong> otro casola salida es:⎧ x1[n / L],n = 0, ± L,± 2L,.....⎧ x[n / L − no], n = 0, ± L,± 2L,.....x1,u[ n]= ⎨= ⎨⎩ 0, <strong>en</strong> otro caso ⎩ 0, <strong>en</strong> otro casosin embargo si calculamos la salida retardada⎧x[(n − no) / L],n = no,no± L,no± 2L,.....xu [ n − no] = ⎨≠ x 1 , u[n]⎩ 0,<strong>en</strong> otro casopor lo que essistema es VARIANTE TEMPORALEj.: Sistema acumuladorn∑y[ n]= x1[λ],ante una <strong>en</strong>trada retardada x[n]=x 1 [n-n o ]yλ=−∞nn−non−no1[ n]= ∑ x1[− no] = ∑ x1[λ']= ∑ x1l'= l−nol=l'λ=−∞λ'=−∞λ=−∞λ [ λ]Si retardamos directam<strong>en</strong>te la salida t<strong>en</strong>emosyn∑ − n0[ n − n o] = x1λ=−∞[ λ ] expresión que coincide con la anterior por lo que elacumulador es un sistema INVARIANTE TEMPORALINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>23 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Sistemas LIT (LTI)Es un sistema que verifica simultáneam<strong>en</strong>te las propiedades de linealidad einvarianza temporal.Estos <strong>sistemas</strong> son s<strong>en</strong>cillos de caracterizar matemáticam<strong>en</strong>te y por tantofáciles de usar. Un gran número de algoritmos de procesado digital deseñales han sido diseñados utilizando este tipo de <strong>sistemas</strong>. Son los queestudiaremos más det<strong>en</strong>idam<strong>en</strong>te <strong>en</strong> capítulos posteriores.Ej: el sistema acumuladorSistemas Causal (LTI)Es aquel <strong>en</strong> el que la salida <strong>en</strong> un determinado instante n o (y[n o ]) dep<strong>en</strong>desolo de muestras de <strong>en</strong>trada <strong>en</strong> instantes n ≤ noy/o salidas <strong>en</strong> instantesanteriores n < no, pero no de <strong>en</strong>tradas posteriores n > no(SISTEMA NOANTICIPATIVO)Ej.: Sistemas causalesy n]= α x[n]+ α x[n −1]+ α x[n − 2] + α x[n[1 234−y [ n]= y[n −1]+ x[n]Sistema acumulador.Promediado móvil.Ej.: Sistemas no causales1y n]= x [ n]+ ( x [ n −1]+ x [ n + 1])[u 2y[n]= x[ − n]uEjercicio: Determina si el sistema y n]= x[ − n]causal ?u3][ es invariante temporal. ¿EsEn muchas ocasiones un sistema no causal puede transformarse <strong>en</strong> unocausal retardando las señales un determinado número de muestras. Así el1sistema no causal y[ n]= xu[n]+ ( x [ n −1]+ x [ n + 1])2 uuse puede transformar <strong>en</strong>1y n]= x [ n −1]+ ( x [ n − 2] x [ n]).[u 2 u+uINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>24 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Sistemas estable BIBOUn sistema se dice que es estable BIBO (Bounded Input Bounded Output)si ante cualquier <strong>en</strong>trada acotada x[ n]≤ Bx< ∞ − ∞ < n < ∞ , la salida estatambién acotada y[ n]≤ By< ∞ − ∞ < n < ∞ .Ej. Promediado Móvil de M múestras:M∑ − 11Mk = 0y [ n]= x[n − k], si x[ n]≤ Bx<strong>en</strong>toncesM −1M −1111y [ n]= ∑ x[n − k]≤ ∑ x[n − k]≤ ( MBx) ≤ Bx< ∞ ESTABLEMMMk = 0Ej: y[] n log( x[]n )k = 0= , aunque se verifique x[ n]≤ Bx, la salida no está acotadapara todas aquellas secu<strong>en</strong>cias que t<strong>en</strong>gan muestras iguales a 0. Ya que <strong>en</strong>estos puntos el logaritmo se hace infinito.Sistemas sin memoria o estáticos.Es aquel <strong>en</strong> el que la salida solo dep<strong>en</strong>de de <strong>en</strong>tradas actuales.En caso contrario se dice que el sistema ti<strong>en</strong>e memoria o es DINÁMICO.Ej:y[] n sin( x[]n )= Sistema sin memoria1∑ N − 1N k = o[] n = x[ n − k]y Sistema con memoria.Sistemas Pasivos.Son aquellos <strong>en</strong> los que para cualquier secu<strong>en</strong>cia de <strong>en</strong>trada x[n] de <strong>en</strong>ergíafinita, la salida ti<strong>en</strong>e como máximo la misma <strong>en</strong>ergía∞∑y[n]∞≤ ∑ x[n]n= −∞n=−∞22< ∞Cuando <strong>en</strong> la expresión anterior se verifica la igualdad se dice que elsistema es SIN PÉRDIDAS (LOSSLESS)INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>25 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Ej.El sistema y[ n]= α x[n − N], con N un <strong>en</strong>tero positivo.La <strong>en</strong>ergía vi<strong>en</strong>e dada por∞∑n=−∞para α ≤1y sin pérdidas para α = 1∞∑2 22y[ n]= α x[n]luego el sistema es pasivon=−∞Respuesta impulsional.La respuesta de un sistema ante una <strong>en</strong>trada x[ n] δ [ n]respuesta impulsional y la d<strong>en</strong>otaremos por h [ n].Respuesta escalón.La respuesta de un sistema ante una <strong>en</strong>trada [ n] u[ n]respuesta escalón y la d<strong>en</strong>otaremos por s [ n]Ej: Respuesta impulsional= se d<strong>en</strong>ominax = se d<strong>en</strong>ominay[ n]= α1x[n]+ α2x[n −1]+ α3x[n − 2] + α4x[n − 3]x n = δ n t<strong>en</strong>emoshaci<strong>en</strong>do [] []h n]= α δ[n]+ α δ[n −1]+ α δ[n − 2] + α δ[n 3] que podemos expresar como[1 234−{ h [ n]}= { α1,α2,α3,α4}↑Respuesta impulsional del sistema acumuladoryn[ n]= ∑ x[λ], haci<strong>en</strong>do x[] n δ [ n]λ=−∞n= t<strong>en</strong>emosh[ n]= ∑δ [ λ]= u[n]que es una de las definiciones de función escalón.λ=−∞CARACTERIZACIÓN TEMPORAL DE LOS SISTEMAS LTI.Como consecu<strong>en</strong>cia de las propiedades de linealidad e invarianza temporalla relación <strong>en</strong>trada salida para un sistema de estas características estácompletam<strong>en</strong>te especificada por su respuesta impulsional.Luego si conocemos la respuesta impulsional de un sistema LTI podemosconocer la respuesta del mismo ante cualquier <strong>en</strong>trada.INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>26 JUAN GÓMEZ SANCHIS CURSO 2009-2010
La justificación es s<strong>en</strong>cilla, ya que cualquier <strong>en</strong>trada la podemos ponercomo una suma de impulsos retardados y por ser el sistema LTI podemoscalcular la salida para cada uno de estos impulsos retardados, queproporcionarán salidas retardadas el mismo número de muestras (por serInvariante temporal) y posteriorm<strong>en</strong>te sumar las salidas ya que se verificael principio de superposición (sistema Lineal).Para una <strong>en</strong>trada g<strong>en</strong>érica expresada como suma de impulsos retardados:∑ ∞k = −∞x [ n]= x[k]δ [ n − k]Si el sistema es LTI ante una <strong>en</strong>trada x[ k]δ [ n − k]la salida será x[ k]h[n − k]luego la salida total seráque podemos expresar como∑ ∞k = −∞y [ n]= x[k]h[n − k]∑ ∞k = −∞y [ n]= x[n − k]h[k]haci<strong>en</strong>do un cambio de índices <strong>en</strong> el sumatorioLa expresión:∞∑k=−∞∞∑y [ n]= x[k]h[n − k]= x[n − k]h[k]k=−∞se d<strong>en</strong>omina SUMA DE CONVOLUCIÓN de las secu<strong>en</strong>cia x[n] y h[n] yse repres<strong>en</strong>ta de forma compacta como:[ n] = x[ n] h[ n]y *Expresión muy importante ya que permite calcular la salida de un sistemaLTI ante cualquier <strong>en</strong>trada, conoci<strong>en</strong>do su respuesta impulsional.Propiedades:Conmutativa: x [] n * h[] n = x[ n] * h[ n]Asociativa: ( x [] n * h[]n )*s[ n] = x[ n] *( h[ n] * s[ n])Distributiva respecto de la suma: ( x [ n] + h[ n])* s[ n] = x[ n] * s[ n] + h[ n] * s[ n]INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>27 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Interpretación y cálculo de la suma de convolución:1. Invertir temporalm<strong>en</strong>te la secu<strong>en</strong>cia h[k] para obt<strong>en</strong>er h[-k].2. Desplazar h[-k] n muestras a la derecha si n>0 o hacia la izda si n
<strong>3.</strong> Convolución de secu<strong>en</strong>cias infinitas Aplicar la definición.INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>29 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Podemos hacer los cálculos mediante la sigui<strong>en</strong>te tabla.N1+ NM21+ M2↓↓n -3 -2 -1 0 1 2 3 4 5 6 7 8x(n) -2 0 1 -1 3h(n) 1 2 0 -1h(-n) -1 0 2 1h(1-n) -1 0 2 1h(2-n) -1 0 2 1h(3-n) -1 0 2 1h(4-n) -1 0 2 1h(5-n) -1 0 2 1h(6-n) -1 0 2 1h(7-n) -1 0 2 1h(8-n) -1 0 2 1y(n)=x(n)*h(n) 0 0 0 -2 -4 1 3 1 5 1 -3 0La última fila conti<strong>en</strong>e los productos acumulados.Ejercicio: Calcula la salida de un sistema LTI con respuesta impulsionalnh( n)= a u( n) a < 1 ante una <strong>en</strong>trada escalón unidad.Ejemplo: Calcula la salida al convolucionar cualquier secu<strong>en</strong>cia conδ ( n − n 0)INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>30 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Repres<strong>en</strong>tación gráfica del cálculo de la convolución:Extraído de: Tratami<strong>en</strong>to Digital de Señales. J.G. ProakisEj:y [ 3] = x[0]h[3]+ x[1]h[2]+ x[2]h[1]+ x[3]h[0]= 2 + 0 + 0 + 1 = 3y [ 5] = x[2]h[3]+ x[3]h[2]+ x[4]h[1]= −1+0 + 6 = 5y [ 7] = x[4]h[3]= −3Regla:Para el calculo de la salida y(n), interv<strong>en</strong>drán todos los productos x(n) h(nk)cuya suma de términos sea n. Ej y(3) intervi<strong>en</strong><strong>en</strong> los productosx(0)h(3)x(1)h(2), x(2)y(1),x(3)h(0)INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>31 JUAN GÓMEZ SANCHIS CURSO 2009-2010
La convolución de una secu<strong>en</strong>cia de longitud N y una de longitud M es unasecu<strong>en</strong>cia de longitud N+M-1En Matlab la función y=conv(a,b) realiza la convolución de dos secu<strong>en</strong>ciasEj: La convolución puede utilizarse para calcular el producto <strong>en</strong>trepolinomios.Interconexión de <strong>sistemas</strong>:Serie o Cascada:Se verifica: h n]= h [ n]*h [ ][1 2nPropiedades:La interconexión de <strong>sistemas</strong> <strong>en</strong> serie es conmutativa, de acuerdo con laspropiedades de la convolución.La interconexión de <strong>sistemas</strong> estables es un sistema estable.Si la conexión de dos <strong>sistemas</strong> verifica h n]*h [ n]= δ ( n)[21 se dice que elsistema h [ ] es el inverso de h [ ] y viceversa1 n2nEjemplo de aplicación: Ecualización de canalesINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>32 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Ejercicio: Un sistema causal ti<strong>en</strong>e por respuesta impulsional una secu<strong>en</strong>ciaescalón. Determina su sistema inverso.Paralelo:Se verifica: h n]= h [ n]+ h [ ][1 2nEjercicio:Determina la respuesta impulsional del sistema resultante de la sigui<strong>en</strong>teinterconexión a partir de las respuestas impulsionales de cada uno de losbloquesh [ n]= δ[n]+ 0.5δ[ n −1]1h [ n]= 0.5δ[ n]− 0.25δ[ n −1]2h [ n]= 2δ[ n]3h [ n]= −2(0.5)4nu[n]Solución: h( n) = δ ( n)ESTABILIDAD BIBO PARA SISTEMAS LTIUn sistema LTI es estable BIBO si y solo si su respuesta impulsional esabsolutam<strong>en</strong>te sumable:Probar como ejercicio.= ∑ ∞ S h[n]n= −∞< ∞INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>33 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Ejemplo: determina para qué valores de α el sigui<strong>en</strong>te sistema LTI esnestable, h[ n]= ( α)u[n]∞∞nn 1S = ∑ α u[n]= ∑ α =si α < 11−αn=−∞n=0Luego si α
Al valor máximo <strong>en</strong>tre N y M se le d<strong>en</strong>omina ORDEN DEL SISTEMA.Aunque estos <strong>sistemas</strong> pued<strong>en</strong> t<strong>en</strong>er una respuesta impulsional finita oinfinita, la salida del sistema siempre puede calcularse ya que esta implicaun número finito de operaciones (M+N+1 productos y M+N sumas)Para calcular la salida del sistema a partir de un instante n=n 0 es necesarioconocer los valores <strong>en</strong> los instantes y[ no− 1 ],y[ no− 2] ,... y[ no− N ], estosvalores son lo que se d<strong>en</strong>ominan CONDICIONES INICIALES DELSISTEMA.Se dice que un sistema está ORIGINALMENTE EN REPOSO oRELAJADO si las condiciones iniciales (ccii) son nulas( y[ no −1 ] = y[ no− 2] = ... = y[ no− N ] = 0 ).Resolución de una ecuación <strong>en</strong> difer<strong>en</strong>cias con coefici<strong>en</strong>tes constantes.Para calcular la salida de un sistema descrito por una ecuación <strong>en</strong>difer<strong>en</strong>cias con coefici<strong>en</strong>tes constante se emplea un procedimi<strong>en</strong>to análogoal utilizado para la resolución de ecuaciones difer<strong>en</strong>ciales con coefici<strong>en</strong>tesconstantes.y( n)= y ( n)y ( n)yhh+p: Solución homogénea. Se obti<strong>en</strong>e considerando x[n]=0, es la soluciónN∑de a y[n − k]= 0k=0kyp: Solución particular. Es la solución específica para nuestra <strong>en</strong>trada( x [] n ≠ 0 ), también se llama solución forzada, ya que la ha provocado la<strong>en</strong>tradaLa suma de ambas soluciones es la solución total y[n](Ver Ejemplos <strong>en</strong> Proakis Pag 100-108)Respuesta a <strong>en</strong>trada nula y respuesta <strong>en</strong> estado nulo.Una forma alternativa de calcular la solución total de una ecuación <strong>en</strong>difer<strong>en</strong>cias es determinando la respuesta ante una <strong>en</strong>trada nula y <strong>en</strong> estadonulo que se defin<strong>en</strong> de la sigui<strong>en</strong>te forma:INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>35 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Respuesta ante <strong>en</strong>trada nula o respuesta natural yzi : es la respuesta delsistema ante una <strong>en</strong>trada nula; es decir, es debida a las condicionesiniciales.Respuesta <strong>en</strong> estado nulo yzs : es la respuesta del sistema ante nuestra<strong>en</strong>trada considerando condiciones iniciales nulas.La respuesta total del sistema se puede escribir como:y[ n] = y [ n] y [ n]zi+Profundizaremos <strong>en</strong> el cálculo de la salida de un sistema ante una <strong>en</strong>tradadeterminada <strong>en</strong> el sigui<strong>en</strong>te capítulo cuando introduzcamos la transformadaZ.CLASIFICACIÓN DE LOS SISTEMA LTI DISCRETOS:Exist<strong>en</strong> diversos criterios de clasificación:Según su respuesta impulsional:• Un sistema cuya respuesta impulsional h[n] ti<strong>en</strong>e un númerofinito de términos no nulosh [ n]= 0 for n < N1 y n > N2,N1< N2se d<strong>en</strong>omina SISTEMA DERESPUESTA IMPULSIONAL FINITA (FIR). Su salida sepuede calcular directam<strong>en</strong>te de la suma de convolución como:y [ n]N∑= 2 k = N1zsh[k]x[n − k]Si comparamos esta ecuación con la expresión g<strong>en</strong>eral de los<strong>sistemas</strong> LTI de coefici<strong>en</strong>tes constantes observamos que h [ k]= bkEj. y n]= α x[n]+ α x[n −1]+ α x[n − 2] + α x[n 3][1 234−• Si la respuesta impulsional no es finita se dice que es unSISTEMA DE RESPUESTA IMPULSIONAL INFINITA(IIR)y n = y n −1+ x nEj.: [] [ ] []INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>36 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Según el procedimi<strong>en</strong>to para calcular su salida:• NO RECURSIVOS. Son aquellos <strong>en</strong> los que la salida se puedecalcular secu<strong>en</strong>cialm<strong>en</strong>te conoci<strong>en</strong>do únicam<strong>en</strong>te las <strong>en</strong>tradasy n = F( x n , x n −1,..., x n − N )pres<strong>en</strong>tes y pasadas. [ ] [ ] [ ] [ ]Ej: y n]= α x[n]+ α x[n −1]+ α x[n − 2] + α x[n 3][1 234−• RECURSIVOS. Son aquellos <strong>en</strong> los que la salida <strong>en</strong> un instantedado dep<strong>en</strong>de de <strong>en</strong>tradas pres<strong>en</strong>tes y pasadas y también dey n = F( x n , x n −1 ,..., x n − M , y n −1,..., y n − N )salidas pasadas. [ ] [ ] [ ] [ ] [ ] [ ]Ej: y [] n = y[ n −1] + x[]nUN SISTEMA IIR SIEMPRE SE IMPLEMENTA DE FORMARECURSIVA, SIN EMBARGO UN SISTEMA RECURSIVO NOSIEMPRE ES DE TIPO IIR.Ej. y [] n = x[] n − x[ n − 4] + y[ n −1]Ejercicio: Calcula la respuesta impulsional del sistema anterior.Según sus coefici<strong>en</strong>tes:• Sistema <strong>en</strong> <strong>tiempo</strong> <strong>discreto</strong> real. Es aquel cuya respuestaimpulsional es REAL.Ej: y [] n = x[] n − x[ n − 4] + y[ n −1]• Sistema <strong>en</strong> <strong>tiempo</strong> <strong>discreto</strong> complejo. Es aquel cuya respuestaimpulsional es COMPLEJA.j• Ej: y[] n = y[ n −1] + e 3x[]nπINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>37 JUAN GÓMEZ SANCHIS CURSO 2009-2010
CORRELACIÓN DE SEÑALESEn ocasiones necesitamos determinar el grado de similitud <strong>en</strong>tre dosseñales. Por ejemplo:Comunicaciones: las señales que se deb<strong>en</strong> transmitir se codifican comosímbolos que posteriorm<strong>en</strong>te deb<strong>en</strong> ser recuperados al pasar por el canal decomunicaciones. El receptor compará las señales recibidas con los patronesde los símbolos que pued<strong>en</strong> ser <strong>en</strong>viados para su detección.Radar y sonar: las señales <strong>en</strong>viadas son reflejadas por el objeto ydevueltas de nuevo al emisor. Comparando estas señales con las originalesse puede obt<strong>en</strong>er información del objeto.SONARRADAREn muchas ocasiones las señales recibidas están contaminadas con ruidoaditivo por lo que la detección es más compleja. La herrami<strong>en</strong>tamatemática para evaluar la similitud <strong>en</strong>tre señales es la CORRELACIÓN.INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>38 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Se define la CORRELACIÓN CRUZADA <strong>en</strong>tre dos secu<strong>en</strong>cia x[n] ey[n] y lo d<strong>en</strong>otamos como r ] a la secu<strong>en</strong>cia:rxyxy [λ[ ] = ∑ ∞ λ x[n]y[n − λ],λ = 0, ± 1, ± 2,...= −∞n• El parámetro λ se d<strong>en</strong>omina desplazami<strong>en</strong>to (lag) y repres<strong>en</strong>ta eldesplazami<strong>en</strong>to temporal <strong>en</strong>tre ambas señales.• La secu<strong>en</strong>cia y[n- λ] se desplaza λ muestras a la derecha respecto dex[n] para λ >0 y λ muestras hacia la izquierda para λ
∞∑n=−∞∞∑r [ λ ] = x[n]y[n − λ]= x[n]y[−(λ−n)]= x *xyn=−∞[] n y[ − n]obt<strong>en</strong>emos que la correlación cruzada <strong>en</strong>tre dos secu<strong>en</strong>cia x[n] e y[n] sepuede obt<strong>en</strong>er mediante la convolución de x[n] con la versión invertidatemporalm<strong>en</strong>te de y[n].x [n]y [ −n]r xy [n]Análogam<strong>en</strong>te para la autocorrelacion de la secu<strong>en</strong>cia x[n]Para el cálculo de la correlación <strong>en</strong>tre dos secu<strong>en</strong>cias podemos utilizar losmismos procedimi<strong>en</strong>tos que para la convolución.Nota: Hay similitudes <strong>en</strong> el cálculo de la correlación y la convolución perosu significado es COMPLETAMENTE DISTINOPROPIEDADES DE LA CORRELACIÓNConsideremos dos secu<strong>en</strong>cias x[n] e y[n] de <strong>en</strong>ergía finita. La <strong>en</strong>ergía deuna combinación lineal de ellas a x[ n]+ y[n − λ]también debe ser finita,calculémosla:∑∞= an=−∞2∑( a x[n]+ y[n − λ])∞n=−∞x [n] x[ −n][n]2x [ n]+ 2a∑2∞=n=−∞x[n]y[n − λ]+Que podemos poner de forma más compacta como:ar2xxrxx[0] + 2a r[0] = Exxy> 0, r[ λ]+ ryyyy[0] = E∑[0] ≥ 0y∞> 0n=−∞y2[ n − λ]≥ 0Observamos que se trata de una ecuación de 2º grado para la variable a.Como se debe verificar la desigualdad para todos los valores de a, laecuación no debe t<strong>en</strong>er ninguna solución real, luego se verificará que:r xxINTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>40 JUAN GÓMEZ SANCHIS CURSO 2009-2010
xx[0] ryy[0] −r2xy[ λ]≥ 0De donde obt<strong>en</strong>emos:| r [ λ ]| ≤ r [0] r [0] =xyxxyyExEyEn el caso particular que x[n]=y[n]| r [ λ ]| ≤ [0] =xxr xxExCONCLUSIÓN: LA SECUENCIA DE AUTOCORRELACIÓNALCANZA SU VALOR MÁXIMO CUANDO EL DESPLAZAMIENTOES CEROLa conclusión anterior indica que una señal se adapta consigo misma pararetardo 0.Para evitar que el resultado de la correlación dep<strong>en</strong>da de las secu<strong>en</strong>ciasconsideradas se defin<strong>en</strong> los coefici<strong>en</strong>tes de autocorrelación y correlaciónnormalizada de la sigui<strong>en</strong>te forma:rxx[λ]Autocorrelación normalizada : ρxx[λ]=rxx[0]rxy[λ]Correlación normalizada : ρxy[λ]=r [0] r [0]Con estas definiciones los coefici<strong>en</strong>tes están acotados al intervalo[ λ] , ρ [ λ] 1−1 ≤ ρ ≤Indep<strong>en</strong>di<strong>en</strong>tem<strong>en</strong>te de las secu<strong>en</strong>cias consideradas.Calculo de la correlación con Matlab:xxxyxxyyAutocorrelación:Correlación cruzada:Coefici<strong>en</strong>te de autocorrelación:Coefici<strong>en</strong>te de correlación:xcorr(x)xcorr(x,y)xcorr(x,’coeff’)xcorr(x,y,’coeff’)INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>41 JUAN GÓMEZ SANCHIS CURSO 2009-2010
Ejercicio:Se define la correlación cruzada de dos secu<strong>en</strong>cias periódicas de periodo NN 11como [ ] = ∑ − rxyλ x[n]y[n − λ],λ = 0, ± 1, ± 2, ... .N n=0Comprueba que la correlación cruzada de dos secu<strong>en</strong>cias periódicas es unasecu<strong>en</strong>cia periódica del mismo período.Ejercicio:Determina la relación exist<strong>en</strong>te <strong>en</strong>tre la autocorrelación de la salida y laautocorrelación de la <strong>en</strong>trada para un sistema LTIEjercicio:Determina la expresión g<strong>en</strong>eral de la autocorrelación de la secu<strong>en</strong>cianx( n)= a u(n)a < 1 y represéntala gráficam<strong>en</strong>te <strong>en</strong> el intervalo [-10,10],para a=0.8. ¿Cuál es la <strong>en</strong>ergía de la señal de <strong>en</strong>trada?Ejercicio:Determina el intervalo de valores para los que el sistema LTI de respuestan⎧an ≥ 0impulsional h[]n = ⎨ a)Es estableb)Es causal.n⎩bn < 0INTRODUCCIÓN. AL PROCESADO DIGITAL DE SEÑALES.MARCELINO MARTÍNEZ SOBER.ANTONIO J. SERRANO LÓPEZ<strong>3.</strong>42 JUAN GÓMEZ SANCHIS CURSO 2009-2010