Trave incastrata agli estremi, gravata di un carico ripartito con ... - Sei

12 Travi iperstatiche 12.1 Travi iperstatiche a una campata
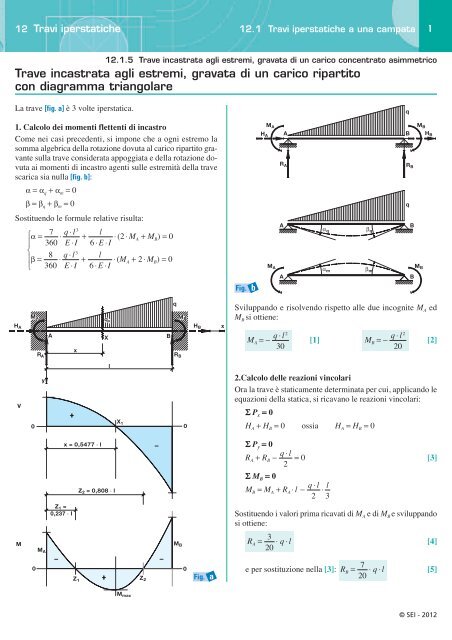
La trave [fig. a] è 3 volte iperstatica.
H A
V
M
M A
R A
y
A
x
12.1.5 Trave incastrata agli estremi, gravata di un carico concentrato asimmetrico
Trave incastrata agli estremi, gravata di un carico ripartito
con diagramma triangolare
1. Calcolo dei momenti flettenti di incastro
Come nei casi precedenti, si impone che a ogni estremo la
somma algebrica della rotazione dovuta al carico ripartito gravante
sulla trave considerata appoggiata e della rotazione dovuta
ai momenti di incastro agenti sulle estremità della trave
scarica sia nulla [fig. b]:
α = αq + αm = 0
β = βq + βm = 0
Sostituendo le formule relative risulta:
α = ⋅ + ⋅(2 ⋅ MA + MB) = 0
q ⋅ l l
β = ⋅ + ⋅(MA + 2 ⋅ MB) = 0
6 ⋅ E ⋅ I
3
q ⋅ l l
6 ⋅ E ⋅ I
8
360 E ⋅ I
3
⎧ 7
⎪ 360 E ⋅ I
⎨
⎪
⎩
q x
X
l
B
q
R B
M B
X1 0 0
0
M A
Z1 =
0,237 ◊ l
x = 0,5477 ◊ l
Z1
Z 2 = 0,808 ◊ l
M max
Z 2
M B
0
H B
Fig. a
x
a)
b)
c)
Fig. b
H A
M A
R A
A B
R B
A B
αq βq q
q
1
M B
H B
MA αm βm MB A B
Sviluppando e risolvendo rispetto alle due incognite M A ed
M B si ottiene:
q ⋅ l
MA =− [1] MB =− [2]
2
q ⋅ l
20
2
30
2.Calcolo delle reazioni vincolari
Ora la trave è staticamente determinata per cui, applicando le
equazioni della statica, si ricavano le reazioni vincolari:
S Px = 0
HA + HB = 0 ossia HA = HB = 0
S Py = 0
q ⋅ l
RA + RB − = 0 [3]
2
S MB = 0
q ⋅ l l
MB = MA + RA⋅ l − ⋅
2 3
Sostituendo i valori prima ricavati di MA e di MBe sviluppando
si ottiene:
3
RA = ⋅ q ⋅ l [4]
20
7
e per sostituzione nella [3]: RB = ⋅ q ⋅ l [5]
20
© SEI - 2012

12 Travi iperstatiche 12.1 Travi iperstatiche a una campata
3. Calcolo della sollecitazione di sforzo di taglio
L’ordinata qx del carico nella sezione generica X a distanza x
da A risulta:
qx =
In tale sezione lo sforzo di taglio vale:
Vx = RA − = ⋅ q ⋅ l − [6]
che è un’equazione di 2° grado, per cui il relativo diagramma
è una parabola.
Per x = 0: Vs A = 0 Vd A = RA = ⋅ q ⋅ l
Per x = l: Vs B = ⋅q⋅l− = − ⋅ q ⋅ l =−RB Uguagliando a zero la [6] si individua la sezione X1 dove V = 0:
q ⋅ x
⋅ q ⋅ l − −0
e risolvendo:
2 q ⋅ x
3
20
3 q ⋅ l 7
20 2 20
3
1
20 2 ⋅ l
2
q ⋅ x
l
qx⋅ x 3
l 20 2 ⋅ l
3
x1 = l ⋅ ≈ 0,5477 ⋅ l
10
4. Calcolo del momento massimo positivo
Nella sezione generica X, con i valori noti, il momento flettente
vale:
q
Mx = MA + RA⋅ x − x⋅ x x
⋅ [7]
2 3
Sostituendo a x il valore prima ricavato relativo alla sezione
ove V = 0 e a MA e RA le relazioni [1] e [4], sviluppando si ottiene:
M + max = 0,021439 ⋅ q ⋅ l 2
12.1.5 Trave incastrata agli estremi, gravata di un carico concentrato asimmetrico
Uguagliando a zero la [7] si individuano le due sezioni Z1 e Z2 di momento nullo ottenendo:
z1 ≈ 0,237 ⋅ l z2≈ 0,808 ⋅ l
[8]
5. Calcolo della freccia nella sezione di mezzeria
L’abbassamento in mezzeria è dato da [fig. c]:
f = f q + f m
l
2
ed essendo:
5
fq = ⋅
768
fm =− ⋅(MA + MB) 16 ⋅ E ⋅ I
sostituendo e sviluppando si ottiene:
q ⋅ l
f = [9]
4
768 ⋅ E ⋅ I
l
2
Fig. c
M A
q ⋅ l 4
E ⋅ I
0l 2
A B
f q
A
A
f l 2
M A MB
A B
fl 2
f m
B
q
q
q
B
MB
2
© SEI - 2012