Successione superiormente limitata Successione inferiormente ...
Successione superiormente limitata Successione inferiormente ...
Successione superiormente limitata Successione inferiormente ...
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
cements<br />
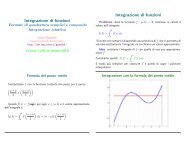
<strong>Successione</strong> <strong>superiormente</strong> <strong>limitata</strong><br />
Def. Una successione an si dice <strong>superiormente</strong> <strong>limitata</strong> se l’insieme<br />
immagine im an = {an, n ≥ n0} è un sottoinsieme di R <strong>superiormente</strong><br />
limitato:<br />
Es.<br />
an<br />
100<br />
0<br />
−100<br />
−200<br />
−300<br />
sup im an = M < +∞ ⇐⇒ sup an = M < +∞<br />
n≥n0<br />
n≥n0<br />
n<br />
0 5 10 15 20<br />
⇐⇒ ∃M ∈ R : an < M, ∀n ≥ n0.<br />
A =im an = n − n 2 , n ∈ N <br />
A = {0, 0, −2, −6, −12, ...}<br />
sup(A) = max(A) = 0.<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.1/9<br />
cements<br />
<strong>Successione</strong> <strong>inferiormente</strong> <strong>limitata</strong><br />
Def. Una successione an si dice <strong>inferiormente</strong> <strong>limitata</strong> se l’insieme<br />
immagine im an = {an, n ≥ n0} è un sottoinsieme di R <strong>inferiormente</strong><br />
limitato:<br />
Es.<br />
an<br />
2.5<br />
2<br />
1.5<br />
1<br />
0.5<br />
inf im an = m > −∞ ⇐⇒ inf an = m > −∞<br />
n≥n0<br />
n≥n0<br />
0<br />
0 5 10 15 20<br />
n<br />
⇐⇒ ∃m ∈ R : an > m, ∀n ≥ n0.<br />
A =im an = n − n 2 , n ∈ N <br />
A =im an = {log(n), n ∈ N+}<br />
A = {0, 0.693.., 1.098.., ...}<br />
inf(A) = min(A) = 0<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.2/9<br />
PSfrag replacements<br />
PSfrag replacements<br />
Def. Una successione si dice <strong>limitata</strong> se è <strong>superiormente</strong> e<br />
<strong>inferiormente</strong> <strong>limitata</strong>.<br />
7n − 2<br />
Esempio. Sia an =<br />
n + 2 .<br />
an<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
−1<br />
0 10 20 30 40 50 60<br />
n<br />
A =im an =<br />
<br />
7n − 2<br />
, n ∈ N<br />
n + 2<br />
inf(A) = min(A) = −1,<br />
sup A = 7.<br />
La successione è <strong>superiormente</strong> ed <strong>inferiormente</strong> <strong>limitata</strong>, quindi è<br />
<strong>limitata</strong>.<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.3/9<br />
Successioni monotòne<br />
Def. Una successione si dice monotona crescente se<br />
an+1 ≥ an<br />
si dice monotona decrescente se<br />
an+1 ≤ an<br />
∀n ≥ n0,<br />
∀n ≥ n0,<br />
Es. an = n<br />
n + 1 , an = n! sono monotone crescenti per n ≥ n0 = 0.<br />
an<br />
1.2<br />
1<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
PSfrag replacements<br />
0<br />
0 1 2 3 4 5 6 7 8 9 10<br />
n<br />
an<br />
10 6<br />
10 4<br />
10 2<br />
10<br />
0 1 2 3 4 5 6 7 8 9 10<br />
0<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.4/9<br />
n
cements<br />
Es. an = 1<br />
n , an<br />
n + 1<br />
= sono monotone decrescenti per n ≥ n0 = 1.<br />
n<br />
an<br />
1.4<br />
1.2<br />
1<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
0<br />
−0.2<br />
PSfrag replacements<br />
n<br />
1 2 3 4 5 6 7 8 9 10<br />
an = 1<br />
n<br />
an<br />
2.4<br />
2.2<br />
2<br />
1.8<br />
1.6<br />
1.4<br />
1.2<br />
1<br />
0.8<br />
n<br />
1 2 3 4 5 6 7 8 9 10<br />
an =<br />
n + 1<br />
n<br />
Es. an = (−1)n<br />
n , an = cos(n) non sono monotone crescenti, né<br />
monotone decrescenti.<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.5/9<br />
Limite di successioni monotone<br />
Teorema Sia {an} una successione monotona, allora essa è<br />
convergente o divergente (non puó essere indeterminata).<br />
In particolare:<br />
se {an} è monotona crescente, ⇒ lim<br />
n→∞ an = sup an<br />
n≥n0<br />
mentre:<br />
se {an} è monotona decrescente, ⇒ lim<br />
n→∞ an = inf an<br />
n≥n0<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.6/9<br />
Osservazione:<br />
⎧<br />
⎪⎨ inf an = min an = an0<br />
n≥n0 n≥n0<br />
se {an} è monotona crescente ⇒<br />
⎪⎩ sup an = lim<br />
n≥n0<br />
n→∞ an<br />
Es. an = n 2 + 3 = {3, 4, 7, 12, ....}.<br />
inf<br />
n≥0 an = min<br />
n≥0 an = a0 = 3 sup<br />
n≥0<br />
an = lim<br />
n→∞ an = +∞.<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.7/9<br />
⎧<br />
⎪⎨ inf an = lim<br />
n≥n0 n→∞<br />
Se {an} è monotona decrescente ⇒<br />
⎪⎩<br />
an<br />
an = max an = an0<br />
n≥n0<br />
Es. an = 2<br />
n =<br />
<br />
inf<br />
n≥1 an = lim<br />
2, 1, 2<br />
3<br />
<br />
1<br />
, , .... .<br />
2<br />
n→∞ an = 0 sup<br />
n≥1<br />
sup<br />
n≥n0<br />
an = max<br />
n≥1 an = a1 = 2.<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.8/9
Il numero e di Nepero. Sia an = 1 + 1<br />
n .<br />
n<br />
n an<br />
1 2.00000000<br />
50 2.69158803...<br />
100 2.70481383...<br />
150 2.70927591...<br />
200 2.71151712...<br />
PSfrag replacements<br />
250 2.71286512...<br />
300 2.71376516...<br />
350 2.71440871...<br />
400 2.71489174...<br />
450 2.71526765...<br />
500 2.71556852...<br />
550 2.71581477...<br />
10000 2.71814592...<br />
y<br />
2.8<br />
2.6<br />
an e<br />
3<br />
2.4<br />
2.2<br />
2<br />
1 21 41 61 81 101 121 141 161 181<br />
E’ possibile dimostrare che an è strettamente crescente e che è<br />
<strong>superiormente</strong> <strong>limitata</strong> (dimostrazione lunga e con molti conti).<br />
Con queste ipotesi, il teorema precedente assicura che la successione<br />
an ha limite (ovvero an è convergente) e si definisce<br />
<br />
e := lim 1 +<br />
n→∞<br />
1<br />
n <br />
= sup 1 +<br />
n n≥1<br />
1<br />
n n<br />
Limiti di successioni Cap3b.pdf c○Paola Gervasio - Analisi Matematica A 2006/2007 - – p.9/9<br />
n