H12_Middelpuntshoeken_en_omtrekshoeken

11
7 OMTREKSHOEK OP EEN HALVE CIRKEL
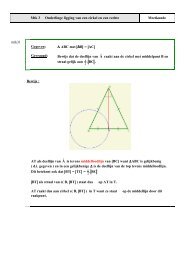
Stelling
Een omtrekshoek van een cirkel waarvan de benen door de grenspunten van
een middellijn gaan, is recht.
We zeggen ook:
– een omtrekshoek die op een halve cirkel staat, is recht.
– vanuit een punt op de cirkel wordt een middellijn onder een rechte hoek
gezien.
Te bewijzen
cirkel met middellijn [AB]
omtrekshoek Pˆ staat op halve cirkel [AB]
Bewijs
ëAPˆ Bë = 1 ⋅ ëAÔBë (stelling van nr. 3)
2
= 1 ⋅ 180°
2
= 90°
} ê ëAPˆ Bë = 90°
A
P
•
?
•
O
B
8 OMGEKEERDE STELLING
Een punt van waaruit een lijnstuk onder een rechte hoek gezien wordt, ligt
op de cirkel met dat lijnstuk als middellijn.
Te bewijzen
ëAPˆ Bë = 90° ê P ligt op de cirkel met middellijn [AB]
Bewijs
We geven een bewijs uit het ongerijmde: we veronderstellen
dat het punt P niet op de cirkel c met
C
P
middellijn [AB] ligt.
Ten minste een van de rechten PA en PB snijdt dan
de cirkel een tweede maal. We onderstellen bv. dat
PA de cirkel een tweede maal snijdt in een punt C
dat verschilt van P.
Verbinden we C met B, dan is Ĉ recht volgens de
rechtstreekse stelling.
In ∆BPC zijn de hoeken Pˆ en Ĉ dus beide recht.
Dat is in strijd met het feit dat de som van de hoekgrootten in een driehoek precies
180° is. Bijgevolg ligt P wel op de cirkel c.
Samenvatting
We kunnen de rechtstreekse stelling van nr. 7 en de omgekeerde stelling van nr. 8
als volgt samenvatten:
De verzameling van de punten van waaruit een lijnstuk onder een rechte
hoek wordt gezien, is de cirkel met dat lijnstuk als middellijn.
A
•
O
B
224