H12_Middelpuntshoeken_en_omtrekshoeken
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
11<br />
Hoofdstuk 11<br />
<strong>Middelpuntshoek<strong>en</strong></strong> <strong>en</strong> omtrekshoek<strong>en</strong><br />
1 MIDDELPUNTSHOEK EN OMTREKSHOEK<br />
Definitie middelpuntshoek<br />
E<strong>en</strong> middelpuntshoek van e<strong>en</strong> cirkel is e<strong>en</strong> hoek waarvan<br />
het hoekpunt het middelpunt van de cirkel is.<br />
De doorsnede van e<strong>en</strong> middelpuntshoek <strong>en</strong> de cirkel is e<strong>en</strong><br />
boog.<br />
We zegg<strong>en</strong>: de middelpuntshoek staat op die boog. In de<br />
figuur hiernaast staat de middelpuntshoek AÔB op de<br />
boog [AB].<br />
O •<br />
A<br />
B<br />
Definitie omtrekshoek<br />
E<strong>en</strong> omtrekshoek van e<strong>en</strong> cirkel is e<strong>en</strong> hoek waarvan het hoekpunt op de<br />
cirkel ligt <strong>en</strong> waarvan beide b<strong>en</strong><strong>en</strong> de cirkel snijd<strong>en</strong> of waarvan één be<strong>en</strong> de<br />
cirkel snijdt <strong>en</strong> één be<strong>en</strong> de cirkel raakt.<br />
B<br />
A<br />
A<br />
•<br />
O<br />
C<br />
•<br />
O<br />
B<br />
De doorsnede van e<strong>en</strong> omtrekshoek <strong>en</strong> de cirkel bestaat uit het hoekpunt <strong>en</strong> e<strong>en</strong><br />
boog. We zegg<strong>en</strong>: de omtrekshoek staat op die boog. In de linkerfiguur staat de<br />
omtrekshoek<br />
<br />
<br />
 op de boog [BC], in de rechterfiguur staat de omtrekshoek  op<br />
de boog [AB].<br />
VRAGEN EN OPDRACHTEN<br />
1 Op welke bog<strong>en</strong> staan de g<strong>en</strong>ummerde hoek<strong>en</strong>?<br />
A<br />
1<br />
A<br />
1<br />
A<br />
1 2<br />
D<br />
•<br />
B<br />
1 D A<br />
1 1<br />
B<br />
C<br />
O<br />
1<br />
B<br />
C<br />
1<br />
B<br />
1<br />
2<br />
C<br />
1 2<br />
3<br />
2<br />
1 C<br />
215
11<br />
2 a Op de onderstaande figuur zijn a, b, c raaklijn<strong>en</strong> aan de cirkel.<br />
Welke van de 13 g<strong>en</strong>ummerde hoek<strong>en</strong> zijn middelpuntshoek<strong>en</strong>, welke zijn<br />
omtrekshoek<strong>en</strong>?<br />
b Welke hoek is met zekerheid e<strong>en</strong> rechte hoek?<br />
c Vind e<strong>en</strong> middelpuntshoek <strong>en</strong> e<strong>en</strong> omtrekshoek die op dezelfde boog staan.<br />
7<br />
b<br />
•<br />
a<br />
•<br />
9<br />
8<br />
•<br />
6<br />
5<br />
12<br />
1<br />
•<br />
13<br />
4<br />
3<br />
10<br />
2<br />
11<br />
c<br />
Antwoord op de vraag van blz. 206.<br />
Slechts 500 m, want na 500 m jaag je die hond het bos uit.<br />
216
11<br />
2 INSTAP<br />
a<br />
Om e<strong>en</strong> vierkant ABCD is e<strong>en</strong> cirkel beschrev<strong>en</strong>.<br />
Het middelpunt O is het snijpunt van de<br />
diagonal<strong>en</strong>.<br />
De omtrekshoek  1<br />
<strong>en</strong> de middelpuntshoek Ô<br />
<br />
1<br />
staan beide op de boog [BC].<br />
Uit de eig<strong>en</strong>schapp<strong>en</strong> van e<strong>en</strong> vierkant kun je<br />
de grootte van  1<br />
<strong>en</strong> Ô 1<br />
afleid<strong>en</strong>.<br />
Vul in :<br />
ë 1 ë = ...... ëÔ 1 ë = ......<br />
B<br />
A<br />
1<br />
1<br />
O<br />
C<br />
D<br />
b Om e<strong>en</strong> gelijkzijdige ∆ABC is e<strong>en</strong> cirkel beschrev<strong>en</strong>.<br />
Het middelpunt O is het snijpunt van<br />
de drie symmetrieass<strong>en</strong>.<br />
De omtrekshoek  <strong>en</strong> de middelpuntshoek Ô<br />
<br />
1<br />
staan beide op de boog [BC].<br />
Uit de eig<strong>en</strong>schapp<strong>en</strong> van e<strong>en</strong> gelijkzijdige driehoek<br />
kun je de grootte van  <strong>en</strong> Ô 1<br />
afleid<strong>en</strong>.<br />
Vul in:<br />
ëÂë = ...... ëÔ 1<br />
ë = ......<br />
B<br />
A<br />
O<br />
1<br />
C<br />
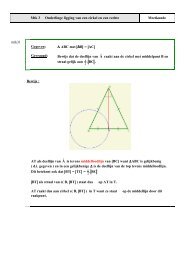
c<br />
In de figuur hiernaast is  e<strong>en</strong> omtrekshoek<br />
<strong>en</strong> Ô e<strong>en</strong> middelpuntshoek.<br />
<br />
Ze staan beide op de boog [BC].<br />
A<br />
•<br />
B<br />
Meet met je geodriehoek nauwkeurig de<br />
grootte van  <strong>en</strong> Ô.<br />
O<br />
C<br />
d Kies op de cirkel hiernaast e<strong>en</strong> boog [BC].<br />
Construeer de middelpuntshoek Ô die op die<br />
boog [BC] staat.<br />
Construeer e<strong>en</strong> omtrekshoek  die op die boog<br />
[BC] staat.<br />
Meet met je geodriehoek nauwkeurig de grootte<br />
van  <strong>en</strong> Ô.<br />
<br />
•<br />
O<br />
e Neem het Cabri-bestand Omtrekshoek<strong>en</strong>1 <strong>en</strong> voer de vermelde opdracht<strong>en</strong> uit.<br />
Leid uit de gevond<strong>en</strong> resultat<strong>en</strong> e<strong>en</strong> vermoed<strong>en</strong> af:<br />
de grootte van e<strong>en</strong> omtrekshoek is ................................. van de grootte van de<br />
middelpuntshoek die op dezelfde boog staat.<br />
217
11<br />
3 STELLING<br />
In e<strong>en</strong> cirkel is e<strong>en</strong> omtrekshoek half zo groot als de middelpuntshoek die op<br />
dezelfde boog staat.<br />
Te bewijz<strong>en</strong><br />
omtrekshoek  <strong>en</strong> middelpuntshoek Ô<br />
} ê<br />
staan beide op de boog [BC]<br />
ëÂë = 1 ⋅ ëÔë<br />
2<br />
Bewijs<br />
Geval 1<br />
Beide b<strong>en</strong><strong>en</strong> van  snijd<strong>en</strong> de cirkel<br />
Ondergeval 1: één be<strong>en</strong> gaat door O<br />
Bewijs nr. 1<br />
ëÔ 1<br />
ë = ëÂë + ëBˆ ë (Ô 1<br />
buit<strong>en</strong>hoek van ∆OAB)<br />
ê ëÔ 1<br />
ë = 2⋅ëÂë (∆OAB gelijkb<strong>en</strong>ig)<br />
ê ëÂë = 1 ⋅ëÔ 1<br />
ë<br />
2<br />
Bewijs nr. 2<br />
B<br />
A<br />
2<br />
O<br />
1<br />
C<br />
ëÂë + ëBˆ ë + ëÔ 2<br />
ë = 180° (som hoekgroott<strong>en</strong> ∆OAB)<br />
ëÂë + ëBˆ ë + 180° – ëÔ 1<br />
ë = 180° (nev<strong>en</strong>hoek<strong>en</strong>)<br />
ëÂë + ëBˆ ë = ëÔ 1<br />
ë<br />
ê 2⋅ëÂë = ëÔ 1<br />
ë (∆OAB gelijkb<strong>en</strong>ig)<br />
ê ëÂë = 1 ⋅ëÔ 1<br />
ë<br />
2<br />
Ondergeval 2: O Ï Â <strong>en</strong> O ligt niet op e<strong>en</strong> be<strong>en</strong><br />
We trekk<strong>en</strong> de halfrechte [AO. Ze verdeelt  in twee hoek<strong>en</strong>  1<br />
<strong>en</strong> Â 2<br />
<strong>en</strong> Ô in<br />
twee hoek<strong>en</strong> Ô 1<br />
<strong>en</strong> Ô 2<br />
. We vind<strong>en</strong> dan:<br />
A<br />
ëBÂCë = ë 1<br />
ë + ë 2<br />
ë<br />
Ondergeval 3: O µ Â<br />
= 1 ⋅ëÔ 1<br />
ë + 1 ⋅ëÔ 2<br />
ë (ondergeval 1)<br />
2 2<br />
= 1 ⋅(ëÔ 1<br />
ë + ëÔ 2<br />
ë)<br />
2<br />
= 1 ⋅ëBÔCë<br />
2<br />
• O<br />
1 2<br />
We trekk<strong>en</strong> de halfrechte [AO <strong>en</strong> noem<strong>en</strong> het tweede snijpunt met de cirkel D. De<br />
hoek BÂD noem<strong>en</strong> we  1<br />
, de hoek CÂD noem<strong>en</strong> we  2<br />
.<br />
Zo noem<strong>en</strong> we ook de hoek<strong>en</strong> BÔD <strong>en</strong> CÔD respectievelijk Ô 1<br />
<strong>en</strong> Ô 2<br />
. We vind<strong>en</strong><br />
dan:<br />
B<br />
1<br />
D<br />
2<br />
C<br />
218
11<br />
ëBÂCë = ë 1<br />
ë – ë 2<br />
ë<br />
= 1 ⋅ëÔ 1<br />
ë – 1 ⋅ëÔ 2<br />
ë (ondergeval 1)<br />
2 2<br />
B<br />
1<br />
A<br />
2<br />
= 1 ⋅(ëÔ 1<br />
ë – ëÔ 2<br />
ë)<br />
•<br />
2<br />
2 O<br />
= 1 1<br />
⋅ëBÔCë<br />
2<br />
C<br />
D<br />
Geval 2 Eén be<strong>en</strong> van  raakt de cirkel <strong>en</strong> één be<strong>en</strong> snijdt de cirkel<br />
Ondergeval 1: één be<strong>en</strong> gaat door O<br />
Je vindt direct:<br />
ë 1<br />
ë = 90°<br />
ëÔ 1<br />
ë = 180°<br />
Bijgevolg: ë 1<br />
ë = 1 ⋅ ëÔ 1<br />
ë<br />
2<br />
(eig. raaklijn)<br />
(gestrekte hoek)<br />
Ondergeval 2: O Ï Â Ondergeval 3: O µ Â<br />
<strong>en</strong> O niet op e<strong>en</strong> be<strong>en</strong><br />
A<br />
1<br />
1 •<br />
O<br />
B<br />
•<br />
A<br />
1<br />
2<br />
B<br />
•<br />
1<br />
A<br />
2<br />
1 • O<br />
2<br />
1<br />
• O<br />
2<br />
C<br />
C<br />
Die ondergevall<strong>en</strong> word<strong>en</strong> bewez<strong>en</strong> zoals de vorige ondergevall<strong>en</strong> 2 <strong>en</strong> 3.<br />
Bijvoorbeeld voor de linkerfiguur:<br />
ëBÂCë = ë 1<br />
ë + ë 2<br />
ë = 1 ⋅ëÔ 1<br />
ë + 1 ⋅ëÔ 2<br />
ë (ondergeval 1)<br />
2 2<br />
= 1 ⋅ (ëÔ 1<br />
ë + ëÔ 2<br />
ë) = 1 ⋅ ëAÔCë<br />
2 2<br />
VRAGEN EN OPDRACHTEN<br />
3 Berek<strong>en</strong> α.<br />
O<br />
α<br />
70°<br />
α<br />
O<br />
60°<br />
O<br />
α<br />
O<br />
α<br />
219
11<br />
O α<br />
26°<br />
102°<br />
O<br />
α<br />
O<br />
α<br />
40°<br />
112°<br />
O<br />
α<br />
4 INSTAP<br />
a<br />
In de figuur hiernaast is a e<strong>en</strong> raaklijn aan de<br />
cirkel; de middelpuntshoek Ô is 70° groot.<br />
B<br />
– Hoe groot is Â? Waarom?<br />
– Hoe groot is Bˆ ? Waarom?<br />
– Hoe groot is Ĉ? Waarom?<br />
– Hoe groot is Pˆ 1 ? Waarom?<br />
Wat kun je besluit<strong>en</strong> over de hoek<strong>en</strong> Â, Bˆ , Ĉ,<br />
Pˆ 1<br />
, die alle op de boog [MP] staan?<br />
<br />
A<br />
M<br />
O<br />
70°<br />
1<br />
P<br />
C<br />
a<br />
b Neem het Cabri-bestand Omtrekshoek<strong>en</strong>1 <strong>en</strong> beweeg alle<strong>en</strong> het punt A. Wat<br />
stel je vast?<br />
5 STELLING<br />
B<br />
Alle omtrekshoek<strong>en</strong> van e<strong>en</strong> cirkel die op<br />
e<strong>en</strong>zelfde boog staan, zijn ev<strong>en</strong> groot.<br />
A<br />
O<br />
C<br />
a<br />
Te bewijz<strong>en</strong><br />
Â, Bˆ , Ĉ, Pˆ 1<br />
zijn omtrekshoek<strong>en</strong><br />
}<br />
ê<br />
die staan op de boog [MP]<br />
Bewijs<br />
Volg<strong>en</strong>s de vorige stelling geldt:<br />
M<br />
ëÂë = ëBˆ ë = ëĈë = ëPˆ 1 ë<br />
1<br />
P<br />
ëÂë = 1 ⋅ ëÔë ëBˆ ë = 1 ⋅ ëÔë ëĈë = 1 ⋅ ëÔë ëPˆ 1 ë = 1 ⋅ ëÔë<br />
2 2 2 2<br />
Dus:<br />
ëÂë = ëBˆ ë = ëĈë = ëPˆ 1 ë<br />
220
11<br />
VRAGEN EN OPDRACHTEN<br />
4 Berek<strong>en</strong> telk<strong>en</strong>s α.<br />
C<br />
B<br />
A<br />
B<br />
31°<br />
α<br />
C<br />
α<br />
A<br />
α<br />
D<br />
A<br />
74°<br />
D<br />
B<br />
C<br />
A<br />
36°<br />
A<br />
58°<br />
A<br />
α<br />
B<br />
α<br />
C<br />
α<br />
B<br />
B 70°<br />
C<br />
C<br />
5 Berek<strong>en</strong> telk<strong>en</strong>s α.<br />
α<br />
57°<br />
O<br />
65°<br />
O<br />
α<br />
α<br />
α<br />
α<br />
α<br />
110°<br />
O<br />
118°<br />
α<br />
O<br />
70°<br />
36°<br />
α<br />
6 Welke g<strong>en</strong>ummerde hoek<strong>en</strong> zijn ev<strong>en</strong> groot?<br />
B D<br />
1 B<br />
C<br />
1 1 1<br />
1<br />
2 1<br />
2<br />
3 2<br />
S<br />
2 4<br />
A<br />
S1<br />
2 1<br />
1 A<br />
1 2<br />
3<br />
A<br />
D<br />
2<br />
C 1<br />
1<br />
C<br />
1<br />
B<br />
C<br />
4 1 2<br />
B<br />
3<br />
1 2<br />
1 2 1<br />
3 2<br />
A 4<br />
D<br />
221
11<br />
7 Berek<strong>en</strong> de hoekgroott<strong>en</strong> van ∆ABC.<br />
A<br />
A<br />
A<br />
A<br />
B<br />
O<br />
72°<br />
C<br />
B<br />
O<br />
134°<br />
C<br />
B<br />
104°<br />
O<br />
C<br />
B<br />
106°<br />
114°<br />
O<br />
C<br />
8 De rechte x raakt de cirkel.<br />
Berek<strong>en</strong> α.<br />
A<br />
70°<br />
x<br />
D<br />
α<br />
76°<br />
B<br />
C<br />
9 E<strong>en</strong> vierhoek waarvan de vier hoekpunt<strong>en</strong> op e<strong>en</strong> cirkel ligg<strong>en</strong>, noem<strong>en</strong> we<br />
e<strong>en</strong> koord<strong>en</strong>vierhoek. Bewijs dat de overstaande hoek<strong>en</strong> van e<strong>en</strong> convexe<br />
koord<strong>en</strong>vierhoek supplem<strong>en</strong>tair zijn.<br />
10 E<strong>en</strong> koorde [BC] is de middelloodlijn van e<strong>en</strong> straal [OA] van e<strong>en</strong> cirkel.<br />
Neem e<strong>en</strong> omtrekshoek waarvan de b<strong>en</strong><strong>en</strong> door de gr<strong>en</strong>spunt<strong>en</strong> B <strong>en</strong> C van<br />
die koorde gaan. Berek<strong>en</strong> de grootte van die omtrekshoek.<br />
11 – Construeer e<strong>en</strong> ∆ABC met hoekgroott<strong>en</strong> 60°, 70°, 50°.<br />
– Construeer de omcirkel.<br />
– Construeer de raaklijn<strong>en</strong> in A, B, C aan de cirkel.<br />
– Berek<strong>en</strong> de grootte van de hoek<strong>en</strong> die de zijd<strong>en</strong> van ∆ABC in e<strong>en</strong> hoekpunt<br />
mak<strong>en</strong> met de raaklijn in dat hoekpunt.<br />
12 Vijf punt<strong>en</strong> P, A, B, C, D ligg<strong>en</strong> op e<strong>en</strong> cirkel, zó<br />
dat:<br />
ëAPˆ Bë = ëBPˆ Cë = ëCPˆ Dë = 45°<br />
Bewijs dat ABCD e<strong>en</strong> vierkant is.<br />
13 Door de top A van e<strong>en</strong> gelijkb<strong>en</strong>ige ∆ABC trekk<strong>en</strong> we e<strong>en</strong> rechte die de<br />
boog [BC] van de omcirkel snijdt in e<strong>en</strong> punt D. Bewijs dat DA de bissectrice<br />
van BDˆ C is.<br />
14 De bissectrice van de hoek  van e<strong>en</strong> ∆ABC snijdt de omcirkel e<strong>en</strong> tweede<br />
maal in D.<br />
a Bewijs: ëBDë = ëDCë.<br />
b<br />
<br />
Leid daaruit af dat in e<strong>en</strong> ∆ABC de bissectrice van e<strong>en</strong> hoek <strong>en</strong> de<br />
middelloodlijn van de overstaande zijde elkaar snijd<strong>en</strong> op de omcirkel.<br />
B<br />
A<br />
•<br />
O<br />
45°<br />
45° 45°<br />
•<br />
P<br />
C<br />
D<br />
222
11<br />
15 a Berek<strong>en</strong> x in de volg<strong>en</strong>de figur<strong>en</strong> (in de tweede figuur is AP de raaklijn<br />
in A).<br />
x<br />
A•<br />
3<br />
•<br />
P<br />
C•<br />
4 8<br />
•<br />
D<br />
• B<br />
b Bewijs algeme<strong>en</strong> voor figur<strong>en</strong> zoals in deel a:<br />
linkerfiguur: ëPAë⋅ëPBë = ëPCë⋅ëPDë<br />
rechterfiguur:<br />
ëPAë 2 = ëPBë⋅ëPCë<br />
Zie ook het Cabri-bestand Oef15.<br />
•<br />
B<br />
16 De bissectrice van de hoek  van e<strong>en</strong> ∆ABC snijdt BC in D <strong>en</strong> de omcirkel<br />
e<strong>en</strong> tweede maal in E. Bewijs:<br />
a ëABë⋅ëACë = ëADë⋅ëAEë b ëBEë 2 = ëEDë⋅ëEAë<br />
5<br />
A<br />
•<br />
•<br />
C<br />
x<br />
4<br />
• P<br />
6 INSTAP<br />
a<br />
–We nem<strong>en</strong> e<strong>en</strong> cirkel met middellijn [AB]. Eerst nem<strong>en</strong> we e<strong>en</strong> punt P<br />
binn<strong>en</strong> de cirkel dat niet op [AB] ligt (figuur 1).<br />
Wat voor e<strong>en</strong> soort hoek lijkt Pˆ ? Kies uit scherp, recht of stomp.<br />
Neem zelf e<strong>en</strong> punt Q binn<strong>en</strong> de cirkel <strong>en</strong> niet op [AB].<br />
Wat voor e<strong>en</strong> soort hoek lijkt Qˆ ?<br />
– Herneem de vrag<strong>en</strong> voor punt<strong>en</strong> P <strong>en</strong> Q buit<strong>en</strong> de cirkel (figuur 2).<br />
– Herneem de vrag<strong>en</strong> voor punt<strong>en</strong> P <strong>en</strong> Q op de cirkel <strong>en</strong> verschill<strong>en</strong>d van A<br />
<strong>en</strong> B (figuur 3).<br />
P<br />
•<br />
P<br />
•<br />
P<br />
•<br />
A<br />
•<br />
B<br />
A<br />
•<br />
B<br />
A<br />
•<br />
B<br />
b Neem het Cabri-bestand Omtrekshoek<strong>en</strong>2 <strong>en</strong> voer de vermelde opdracht uit.<br />
Gebruik beide instapp<strong>en</strong> om e<strong>en</strong> vermoed<strong>en</strong> op te stell<strong>en</strong> over de grootte van e<strong>en</strong><br />
omtrekshoek waarvan de b<strong>en</strong><strong>en</strong> door de gr<strong>en</strong>spunt<strong>en</strong> van e<strong>en</strong> middellijn gaan.<br />
223
11<br />
7 OMTREKSHOEK OP EEN HALVE CIRKEL<br />
Stelling<br />
E<strong>en</strong> omtrekshoek van e<strong>en</strong> cirkel waarvan de b<strong>en</strong><strong>en</strong> door de gr<strong>en</strong>spunt<strong>en</strong> van<br />
e<strong>en</strong> middellijn gaan, is recht.<br />
We zegg<strong>en</strong> ook:<br />
– e<strong>en</strong> omtrekshoek die op e<strong>en</strong> halve cirkel staat, is recht.<br />
– vanuit e<strong>en</strong> punt op de cirkel wordt e<strong>en</strong> middellijn onder e<strong>en</strong> rechte hoek<br />
gezi<strong>en</strong>.<br />
Te bewijz<strong>en</strong><br />
cirkel met middellijn [AB]<br />
omtrekshoek Pˆ staat op halve cirkel [AB]<br />
Bewijs<br />
ëAPˆ Bë = 1 ⋅ ëAÔBë (stelling van nr. 3)<br />
2<br />
= 1 ⋅ 180°<br />
2<br />
= 90°<br />
} ê ëAPˆ Bë = 90°<br />
A<br />
P<br />
•<br />
?<br />
•<br />
O<br />
B<br />
8 OMGEKEERDE STELLING<br />
E<strong>en</strong> punt van waaruit e<strong>en</strong> lijnstuk onder e<strong>en</strong> rechte hoek gezi<strong>en</strong> wordt, ligt<br />
op de cirkel met dat lijnstuk als middellijn.<br />
Te bewijz<strong>en</strong><br />
ëAPˆ Bë = 90° ê P ligt op de cirkel met middellijn [AB]<br />
Bewijs<br />
We gev<strong>en</strong> e<strong>en</strong> bewijs uit het ongerijmde: we veronderstell<strong>en</strong><br />
dat het punt P niet op de cirkel c met<br />
C<br />
P<br />
middellijn [AB] ligt.<br />
T<strong>en</strong> minste e<strong>en</strong> van de recht<strong>en</strong> PA <strong>en</strong> PB snijdt dan<br />
de cirkel e<strong>en</strong> tweede maal. We onderstell<strong>en</strong> bv. dat<br />
PA de cirkel e<strong>en</strong> tweede maal snijdt in e<strong>en</strong> punt C<br />
dat verschilt van P.<br />
Verbind<strong>en</strong> we C met B, dan is Ĉ recht volg<strong>en</strong>s de<br />
rechtstreekse stelling.<br />
In ∆BPC zijn de hoek<strong>en</strong> Pˆ <strong>en</strong> Ĉ dus beide recht.<br />
Dat is in strijd met het feit dat de som van de hoekgroott<strong>en</strong> in e<strong>en</strong> driehoek precies<br />
180° is. Bijgevolg ligt P wel op de cirkel c.<br />
Sam<strong>en</strong>vatting<br />
We kunn<strong>en</strong> de rechtstreekse stelling van nr. 7 <strong>en</strong> de omgekeerde stelling van nr. 8<br />
als volgt sam<strong>en</strong>vatt<strong>en</strong>:<br />
De verzameling van de punt<strong>en</strong> van waaruit e<strong>en</strong> lijnstuk onder e<strong>en</strong> rechte<br />
hoek wordt gezi<strong>en</strong>, is de cirkel met dat lijnstuk als middellijn.<br />
A<br />
•<br />
O<br />
B<br />
224
11<br />
VRAGEN EN OPDRACHTEN<br />
17 Welke hoek<strong>en</strong> in deze figuur zijn recht?<br />
Waarom?<br />
B<br />
C<br />
A<br />
• O<br />
D<br />
18 Berek<strong>en</strong> α.<br />
E<br />
• O<br />
=<br />
• O<br />
α<br />
A<br />
19 Construeer e<strong>en</strong> cirkel met middellijn [BC]. Neem op die cirkel e<strong>en</strong> punt A,<br />
verschill<strong>en</strong>d van B <strong>en</strong> C, <strong>en</strong> construeer D = s A<br />
(C). Welk soort driehoek is<br />
∆BCD? Waarom?<br />
20 Neem e<strong>en</strong> lijnstuk [AB]. Noem M het midd<strong>en</strong>.<br />
Construeer e<strong>en</strong> punt C µ AB <strong>en</strong> zó dat: ëCMë = ëAMë = ëMBë<br />
Welk soort driehoek is ∆ABC? Waarom?<br />
21 Op e<strong>en</strong> cirkel met middellijn [AB] nem<strong>en</strong> we twee punt<strong>en</strong> C <strong>en</strong> D zó dat ze<br />
aan dezelfde kant van AB ligg<strong>en</strong>. We gev<strong>en</strong> het snijpunt van AC <strong>en</strong> BD de<br />
naam P <strong>en</strong> het snijpunt van AD <strong>en</strong> BC de naam Q. Welke onderlinge stand<br />
hebb<strong>en</strong> AB <strong>en</strong> PQ. Waarom?<br />
Blijft die eig<strong>en</strong>schap geld<strong>en</strong> als je C <strong>en</strong> D aan weerskant<strong>en</strong> van AB neemt?<br />
22 De cirkel met e<strong>en</strong> opstaande zijde van e<strong>en</strong> gelijkb<strong>en</strong>ige driehoek als middellijn<br />
snijdt de basis in het midd<strong>en</strong>. Bewijs dat.<br />
23 We nem<strong>en</strong> e<strong>en</strong> ∆ABC <strong>en</strong> trekk<strong>en</strong> de cirkels met middellijn<strong>en</strong> [AB] <strong>en</strong> [AC].<br />
Die cirkels snijd<strong>en</strong> elkaar in e<strong>en</strong> merkwaardig punt van [BC]. Welk?<br />
24 De straal van e<strong>en</strong> cirkel meet 2,5 cm. E<strong>en</strong> punt A van die cirkel ligt op 4 cm<br />
van het gr<strong>en</strong>spunt B van e<strong>en</strong> middellijn [BC]. Hoe ver ligt A van C?<br />
25 In de figuur hiernaast is [AB] e<strong>en</strong> middellijn van<br />
de cirkel. Berek<strong>en</strong> x.<br />
D<br />
x<br />
A<br />
•<br />
2 cm C 4,5 cm<br />
B<br />
225
11<br />
26 Berek<strong>en</strong> in de eerste cirkel x, in de tweede α <strong>en</strong> in de derde de straal r.<br />
10<br />
C<br />
A<br />
=<br />
•<br />
O<br />
B<br />
r = 6<br />
27 Twee cirkels c 1<br />
<strong>en</strong> c 2<br />
hebb<strong>en</strong> twee punt<strong>en</strong> A <strong>en</strong> B geme<strong>en</strong>schappelijk.<br />
Construeer de middellijn [AC] van c 1<br />
<strong>en</strong> de middellijn [AD] van c 2<br />
. Bewijs<br />
dat C, B <strong>en</strong> D op één rechte ligg<strong>en</strong>.<br />
28 We nem<strong>en</strong> e<strong>en</strong> ∆ABC <strong>en</strong> de omcirkel c. Construeer het hoogtelijnstuk [AD]<br />
<strong>en</strong> de middellijn [AE].<br />
a Bewijs: ∆ABD & ∆AEC<br />
b Leid daaruit af dat ∆ABC <strong>en</strong> ∆ADE dezelfde bissectrice door A hebb<strong>en</strong>.<br />
c Bewijs: ëABë⋅ëACë = ëADë⋅ëAEë<br />
29 In de figuur is O het middelpunt van de cirkel.<br />
Berek<strong>en</strong> ëADë.<br />
A<br />
12<br />
C<br />
5<br />
O<br />
12<br />
D<br />
B<br />
30 In het gr<strong>en</strong>spunt A van e<strong>en</strong> middellijn [AB] van e<strong>en</strong> cirkel trekk<strong>en</strong> we de<br />
raaklijn. E<strong>en</strong> willekeurige rechte door B snijdt die raaklijn in C <strong>en</strong> de cirkel<br />
e<strong>en</strong> tweede maal in D.<br />
Bewijs: ëADë 2 = ëCDë⋅ëDBë<br />
31 Trek in de onderstaande figur<strong>en</strong> cirkels die telk<strong>en</strong>s door vier van de b<strong>en</strong>oemde<br />
punt<strong>en</strong> gaan.<br />
A<br />
A<br />
E<br />
G<br />
F<br />
H<br />
B<br />
F<br />
C<br />
E<br />
B<br />
D<br />
C<br />
D<br />
226
11<br />
32 Bewijs voor de figuur hiernaast:<br />
ë 1<br />
ë = ëBˆ 1 ë<br />
A<br />
C<br />
D<br />
1 1<br />
B<br />
33 Voor e<strong>en</strong> vierhoek ABCD geldt: ëÂë = ëĈë = 90°.<br />
Heeft die vierhoek e<strong>en</strong> omgeschrev<strong>en</strong> cirkel?<br />
Zo ja, waar ligt het middelpunt?<br />
B<br />
C<br />
A<br />
D<br />
34 Op e<strong>en</strong> rechte x nem<strong>en</strong> we drie punt<strong>en</strong> A, B, C. We nem<strong>en</strong> tev<strong>en</strong>s e<strong>en</strong> punt<br />
P µ x. We noem<strong>en</strong> P’ het voetpunt van de loodlijn uit P op x. Welk punt ligt<br />
op elk van de cirkels met middellijn<strong>en</strong> [PA], [PB], [PC]? Verklaar.<br />
35 Op e<strong>en</strong> cirkel met middellijn [BC] nem<strong>en</strong> we e<strong>en</strong> punt A. We construer<strong>en</strong> het<br />
parallellogram ABCD.<br />
Waar ligt het middelpunt van de omcirkel van ∆ACD? Waarom?<br />
36 Neem e<strong>en</strong> ∆ABC, rechthoekig in A. Noem M het midd<strong>en</strong> van [BC] <strong>en</strong> x de<br />
middelloodlijn van [BC].<br />
Construeer: D = s BC<br />
(A) E = s x<br />
(A) F = s M<br />
(A)<br />
Bewijs dat A, B, C, D, E, F op één cirkel ligg<strong>en</strong>.<br />
37 De hoekpunt<strong>en</strong> A <strong>en</strong> C van e<strong>en</strong> rechthoek ABCD zijn vast, de hoekpunt<strong>en</strong> B<br />
<strong>en</strong> D zijn veranderlijk. Welke figuur wordt beschrev<strong>en</strong> door B? Welke door<br />
D? Verklaar.<br />
38 Welke verzameling vorm<strong>en</strong> de midd<strong>en</strong>s van de koord<strong>en</strong> door e<strong>en</strong> vast punt<br />
van e<strong>en</strong> cirkel? Verklaar. Zie het Cabri-bestand Oef38.<br />
39 Construeer e<strong>en</strong> punt P Ï a<br />
zó dat AP ⊥ PB.<br />
• B<br />
A •<br />
a<br />
40 Gegev<strong>en</strong>: e<strong>en</strong> cirkel met e<strong>en</strong> onbek<strong>en</strong>d middelpunt. Construeer dat punt.<br />
41 Construeer e<strong>en</strong> ∆ABC met ëBCë = 5 cm; de hoogt<strong>en</strong> uit B <strong>en</strong> C met<strong>en</strong> respectievelijk<br />
3 cm <strong>en</strong> 4,7 cm. Eén oplossing volstaat.<br />
42 Met de schuine zijde [BC] van e<strong>en</strong> rechthoekige ∆ABC als zijde construer<strong>en</strong><br />
we buit<strong>en</strong>waarts e<strong>en</strong> vierkant BCDE. Bewijs dat de rechte door A <strong>en</strong> het<br />
snijpunt van de diagonal<strong>en</strong> van BCDE de bissectrice van  is.<br />
227
11<br />
9 RAAKLIJNEN UIT EEN PUNT AAN EEN CIRKEL<br />
We gaan uit van e<strong>en</strong> cirkel c <strong>en</strong> e<strong>en</strong> punt P geleg<strong>en</strong> buit<strong>en</strong> de cirkel.<br />
Gevraagd: e<strong>en</strong> methode om de raaklijn<strong>en</strong> uit P aan c te construer<strong>en</strong>.<br />
Oplossing<br />
We noem<strong>en</strong> O het middelpunt van de cirkel<br />
<strong>en</strong> A e<strong>en</strong> gezocht raakpunt.<br />
c<br />
A<br />
•<br />
Dan geldt (eig<strong>en</strong>schap van de raaklijn in<br />
e<strong>en</strong> punt van de cirkel):<br />
OA ⊥ AP<br />
Het lijnstuk [OP] wordt dus vanuit A<br />
onder e<strong>en</strong> rechte hoek gezi<strong>en</strong>.<br />
O •<br />
• P<br />
Volg<strong>en</strong>s de stelling van nr. 8 betek<strong>en</strong>t dat:<br />
c'<br />
A<br />
A ligt op de cirkel met middellijn [OP].<br />
•<br />
c<br />
Daaruit volgt de constructie:<br />
– construeer de cirkel c’ met middellijn<br />
[OP]<br />
O•<br />
•<br />
M<br />
• P<br />
– de rechte door P <strong>en</strong> e<strong>en</strong> snijpunt van de<br />
•<br />
cirkels c <strong>en</strong> c’ is e<strong>en</strong> raaklijn uit P aan<br />
B<br />
de cirkel c.<br />
Je stelt vast: uit e<strong>en</strong> punt buit<strong>en</strong> e<strong>en</strong> cirkel kunn<strong>en</strong> precies twee raaklijn<strong>en</strong> aan die<br />
cirkel getrokk<strong>en</strong> word<strong>en</strong>.<br />
Opmerking<br />
De rechte OP gaat door de middelpunt<strong>en</strong> O <strong>en</strong> M van de cirkels c <strong>en</strong> c’ <strong>en</strong> is dus<br />
e<strong>en</strong> symmetrieas van de hele figuur. Daaruit volgt:<br />
PO ⊥ AB ëPAë = ëPBë OP bissectrice van AÔB <strong>en</strong> van APˆ B<br />
VRAGEN EN OPDRACHTEN<br />
43 Neem e<strong>en</strong> cirkel c <strong>en</strong> e<strong>en</strong> punt P buit<strong>en</strong> de cirkel. Construeer de raaklijn<strong>en</strong><br />
uit P aan c.<br />
44 We nem<strong>en</strong> twee cirkels c 1<br />
<strong>en</strong> c 2<br />
met middelpunt<strong>en</strong> O 1<br />
<strong>en</strong> O 2<br />
, zó dat c 1<br />
<strong>en</strong> c 2<br />
ge<strong>en</strong> <strong>en</strong>kel punt geme<strong>en</strong>schappelijk hebb<strong>en</strong>.<br />
Construeer de raaklijn<strong>en</strong> uit O 1<br />
aan c 2<br />
<strong>en</strong> noem de raakpunt<strong>en</strong> A <strong>en</strong> B.<br />
Construeer de raaklijn<strong>en</strong> uit O 2<br />
aan c 1<br />
<strong>en</strong> noem de raakpunt<strong>en</strong> C <strong>en</strong> D.<br />
Bewijs dat O 1<br />
, O 2<br />
, A, B, C, D op één cirkel ligg<strong>en</strong>.<br />
45 Uit e<strong>en</strong> punt P geleg<strong>en</strong> op 25 cm van het middelpunt O van e<strong>en</strong> cirkel met<br />
straal 10 cm trekk<strong>en</strong> we beide raaklijn<strong>en</strong> aan die cirkel.<br />
a Hoe ver ligt P van de raakpunt<strong>en</strong> A <strong>en</strong> B?<br />
b Berek<strong>en</strong> de afstand tuss<strong>en</strong> de raakpunt<strong>en</strong>.<br />
c Berek<strong>en</strong> de grootte van de scherpe hoek tuss<strong>en</strong> de raaklijn<strong>en</strong>.<br />
228
11<br />
WE ONTHOUDEN<br />
Middelpuntshoek <strong>en</strong> omtrekshoek<br />
E<strong>en</strong> middelpuntshoek van e<strong>en</strong> cirkel is e<strong>en</strong> hoek<br />
waarvan het hoekpunt het middelpunt van de<br />
cirkel is.<br />
•<br />
A<br />
B<br />
E<strong>en</strong> omtrekshoek van e<strong>en</strong> cirkel<br />
is e<strong>en</strong> hoek waarvan het<br />
hoekpunt op de cirkel ligt <strong>en</strong><br />
waarvan beide b<strong>en</strong><strong>en</strong> de cirkel<br />
snijd<strong>en</strong> of waarvan één<br />
be<strong>en</strong> de cirkel snijdt <strong>en</strong> één<br />
be<strong>en</strong> de cirkel raakt.<br />
A<br />
•<br />
O<br />
B<br />
C<br />
A<br />
•<br />
O<br />
B<br />
Stelling<strong>en</strong><br />
1 In e<strong>en</strong> cirkel is e<strong>en</strong> omtrekshoek half zo groot als<br />
de middelpuntshoek die op dezelfde boog staat.<br />
Bv. voor de figuur hiernaast: ëÂë = 1 ⋅ ëÔ 1<br />
ë<br />
2<br />
A<br />
•<br />
O<br />
1<br />
2 Alle omtrekshoek<strong>en</strong> van e<strong>en</strong> cirkel die op e<strong>en</strong>zelfde<br />
boog staan, zijn ev<strong>en</strong> groot.<br />
Bv. voor de figuur hiernaast:<br />
A<br />
B<br />
C<br />
ëÂë = ëBˆ ë = ëĈë = ëDˆ 1 ë<br />
1<br />
D<br />
3 E<strong>en</strong> omtrekshoek van e<strong>en</strong> cirkel waarvan de<br />
b<strong>en</strong><strong>en</strong> door de gr<strong>en</strong>spunt<strong>en</strong> van e<strong>en</strong> middellijn<br />
gaan, is recht.<br />
A<br />
4 Omgekeerd: e<strong>en</strong> punt van waaruit e<strong>en</strong> lijnstuk<br />
onder e<strong>en</strong> rechte hoek gezi<strong>en</strong> wordt, ligt op de<br />
cirkel met dat lijnstuk als middellijn.<br />
B<br />
• O<br />
C<br />
De raaklijn<strong>en</strong> uit e<strong>en</strong> punt P aan<br />
e<strong>en</strong> cirkel c construer<strong>en</strong><br />
c<br />
A<br />
c'<br />
– construeer de cirkel c’ met<br />
middellijn [OP]<br />
– de rechte door P <strong>en</strong> e<strong>en</strong> snijpunt<br />
van de cirkels c <strong>en</strong> c’ is e<strong>en</strong> raaklijn<br />
uit P aan de cirkel c.<br />
O•<br />
B<br />
• • P<br />
M<br />
229
11<br />
TOETS JEZELF<br />
1 Berek<strong>en</strong> α. In de laatste figuur is x e<strong>en</strong> raaklijn.<br />
C<br />
O 78 o<br />
=<br />
A<br />
B<br />
C<br />
D<br />
32 o A<br />
=<br />
B<br />
B<br />
O<br />
•<br />
54 o<br />
=<br />
A<br />
B<br />
A<br />
=<br />
70 o<br />
x<br />
C<br />
C<br />
2 Berek<strong>en</strong> de hoekgrootte van:<br />
a ∆ABC b ∆OAB<br />
D<br />
67 o A<br />
C<br />
B<br />
A<br />
B<br />
O<br />
114 o<br />
C<br />
3 In e<strong>en</strong> ∆ABC is O het snijpunt van de middelloodlijn<strong>en</strong> <strong>en</strong> M het midd<strong>en</strong> van<br />
[BC]. Bewijs: ëÂë = ëBÔMë<br />
4 De cirkels c <strong>en</strong> c’ hebb<strong>en</strong> de punt<strong>en</strong> A <strong>en</strong> B geme<strong>en</strong>schappelijk. Door A is e<strong>en</strong><br />
rechte getrokk<strong>en</strong> die c e<strong>en</strong> tweede maal snijdt in C <strong>en</strong> c’ e<strong>en</strong> tweede maal in D.<br />
Door A is nog e<strong>en</strong> rechte getrokk<strong>en</strong> die c e<strong>en</strong> tweede maal snijdt in E <strong>en</strong> c’ e<strong>en</strong><br />
tweede maal in F.<br />
Bewijs: ëCBˆ Eë = ëDBˆ Fë<br />
E<br />
A<br />
1 2<br />
D<br />
C<br />
F<br />
c<br />
B<br />
c'<br />
230
11<br />
5 Op e<strong>en</strong> cirkel c met middellijn [BC] ligt e<strong>en</strong><br />
punt A op 24 mm van B <strong>en</strong> op 70 mm van C.<br />
a Berek<strong>en</strong> de straal van de cirkel.<br />
b Berek<strong>en</strong> de hoekgrootte van Bˆ <strong>en</strong> Ĉ<br />
(afrond<strong>en</strong> op 0,1°).<br />
B<br />
A<br />
24<br />
70<br />
c<br />
C<br />
6 We nem<strong>en</strong> e<strong>en</strong> gelijkzijdige ∆ABC <strong>en</strong> construer<strong>en</strong><br />
D = s C<br />
(B).<br />
Welk soort driehoek is ∆ABD?<br />
Verklaar.<br />
A<br />
B C D<br />
7 In e<strong>en</strong> scherphoekige ∆ABC noem<strong>en</strong> we D het voetpunt van de hoogtelijn uit<br />
A <strong>en</strong> E het voetpunt van de hoogtelijn uit B. Het snijpunt van AD <strong>en</strong> BE noem<strong>en</strong><br />
we H.<br />
Bewijs: ëDĤCë = ëDÊCë Maak zelf e<strong>en</strong> figuur.<br />
Tip: zoek e<strong>en</strong> cirkel die door vier van de punt<strong>en</strong> A, B, C, D, E, H gaat.<br />
231